Основные этапы развития математического аппарата квантовой электродинамики.

Процесс создания математического аппарата современной квантовой электродинамики условно можно разделить на четыре этапа.

На первом этапе был создан аппарат квантованного электромагнитного поля излучения (поле, не взаимодействующее с источниками). На втором — построена математическая теория квантованного электронно-позитронного поля (квантование источников поля). На третьем — описано взаимодействие указанных полей в рамках теории возмущений в первом ее приближении. Наконец, на четвертом этапе был создан аппарат, характеризующий взаимодействие квантованных электромагнитного и электронно-позитронного полей с учетом второго и последующих приближений теории возмущений (был развит метод перенормировок, позволяющий осуществить описание взаимодействующих полей в высших порядках теории возмущений).

Каждый из указанных этапов складывался, в свою очередь, из ряда логически необходимых ступеней, приводящих к соответствующим уравнениям квантовой электродинамики. С этой точки зрения, например, первый этап — построение аппарата свободного квантованного электромагнитного поля — мог быть осуществлен только благодаря предварительному исследованию квантовых свойств излучения[41]. На этой основе сформировалось представление об электромагнитном поле излучения как об особой квантовой системе, которая обладает, с одной стороны, континуальными характеристиками (частота, волновой вектор), а с другой — может быть представлена как набор фотонов, находящихся в различных квантовых состояниях. В аспекте волновых свойств поле по традиции описывалось уравнениями Максвелла. Поэтому возникала задача таким образом видоизменить эти уравнения, чтобы учесть и корпускулярные свойства свободного электромагнитного поля.

Для этой цели величины, связанные в уравнениях Максвелла, по аналогии с уже привычным квантовомеханическим подходом были рассмотрены в качестве операторов, подчиняющихся определенным перестановочным соотношениям. Таким путем уравнения Максвелла преобразовывались в уравнения квантованного электромагнитного поля. Взятые совместно с правилами коммутации для операторов (перестановочными соотношениями) они составили математический аппарат, описывающий это поле[42].

Следующий шаг исследования микроструктуры электромагнитных процессов предполагал учет взаимодействия поля излучения с квантованными источниками (плотностями заряда-тока). Для этого было необходимо развить математический формализм, описывающий квантовые свойства системы электронов в релятивистской области. Решение такой задачи, в свою очередь, привело к представлениям об электронно-позитронном поле. В результате исходная проблема квантования источников электромагнитного поля была переформулирована в проблему математического описания квантовых свойств электронно-позитронного поля. Ее решение знаменовало второй этап разработки аппарата квантовой электродинамики.

С точки зрения логики познавательного движения исходным пунктом этого этапа следует считать построение Дираком релятивистской квантовой механики электрона. Нам хотелось бы еще раз обратить внимание на то обстоятельство, что теория Дирака, открывшая физике область электронно-позитронных взаимодействий, послужила своего рода промежуточным “блоком” знаний для построения современной квантовой электродинамики. Это был характерный пример того, как по ходу теоретического синтеза вводятся недостающие звенья (частные теоретические схемы и законы), которые обеспечивают успешное продвижение к будущим фундаментальным уравнениям создаваемой теории.

Обобщение уравнений Дирака было связано с процедурой квантования электронно-позитронного поля. Этот объект, введенный в рамках релятивистской квантовой механики электрона, был рассмотрен так же, как в свое время рассматривалось подлежащее квантованию электромагнитное поле излучения. Он был представлен в качестве некоторой целостной динамической системы, обладающей одновременно волновыми и корпускулярными свойствами. Квантовая природа этой системы описывалась путем введения операторов, действующих на волновую функцию (вектор состояния) системы, которая была определена как функция в пространстве чисел заполнения (соответствующих числам частиц — электронов и позитронов, находящихся в определенных квантовых состояниях и образующих электронно-позитронное поле). 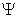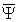В качестве основных операторов поля были рассмотрены волновые функции (х) и (х), характеризовавшие состояние электронов и позитронов в уравнениях Дирака. Действие этих операторов на вектор состояния поля меняло числа заполнения, что соответствовало описанию поля в терминах рождения и уничтожения электронов и позитронов в определенных квантовых состояниях[43].

Таким путем была создана математическая теория свободного квантованного электронно-позитронного поля. Представление о таком поле потребовало по-новому сформулировать проблему теоретического описания квантованного электромагнитного поля, взаимодействующего с источниками. Она предстала теперь как проблема взаимодействия соответствующих квантованных полей.

Основы математического аппарата, описывающего это взаимодействие, были найдены на третьем этапе формирования квантовой электродинамики. Указанный аппарат представлял собой систему уравнений, объединяющих уравнения для квантованного электромагнитного и электронно-позитронного полей (уравнения Максвелла и Дирака для операторов соответствующих полей). Кроме того, он включал методы их приближенного решения с помощью теории возмущений, которая была развита еще в рамках нерелятивистской квантовой механики, а затем перенесена на область взаимодействия квантованных полей. Такое взаимодействие изображается в квантовой электродинамике как рассеяние соответствующих частиц (электронов, позитронов и фотонов), связанное с их взаимными превращениями[44]. Первоначально были описаны процессы рассеяния только в первом приближении теории возмущений. На этой основе была построена теория взаимодействия квантованного электромагнитного поля с зарядами, позволявшая описать и объяснить два типа процессов: 1) переходы электрона (или позитрона) из одного состояния в другое с испусканием фотона и 2) образование или поглощение пары электрон — позитрон, сопровождаемое поглощением или рождением фотонов.

Попытки исследовать взаимодействие квантованного электромагнитного и электронно-позитронного полей в других приближениях теории возмущений не только не уточнили ранее полученные результаты, но и привели к математически бессмысленным выражениям. Для наблюдаемых величин, характеризующих электроны и позитроны, например для заряда, массы и других связанных с ними величин, получались бесконечные выражения, имеющие вид расходящихся интегралов.

Задача построения математического аппарата, учитывающего высшие приближения теории возмущений, была решена только на четвертом, заключительном этапе эволюции квантовой электродинамики. В работах С. Томанага, Е. Швингера. Р. Фейнмана. Ф. Дайсона теория возмущений была развита в релятивистски инвариантном виде и был предложен метод перенормировок, устраняющий расходимости путем замены формально вычисляемых бесконечных значений физических величин конечными значениями, известными из опыта.

В результате значительно расширился круг процессов, описываемых и объясняемых квантовой электродинамикой. Стало возможным решить задачи по рассеянию электрона электроном, фотона — электроном, предсказать взаимодействие электрона с вакуумом, рассеяние фотона на фотонах и т. д.

Так выглядит история квантовой электродинамики, если рассмотреть ее в аспекте формирования математического аппарата. Нетрудно проследить отчетливо выраженную внутреннюю логику его построения: вначале создавался формализм, описывающий свободные квантованные поля, а затем на этой основе строился аппарат, характеризующий взаимодействие полей.

Внешне весь этот процесс (по крайней мере в основной своей части) выглядит как серия математических экстраполяций, приводящих к системе уравнений для взаимодействующих квантованных полей и методам решения таких уравнений. Блестящие достижения квантовой электродинамики могут быть истолкованы как еще одно свидетельство эффективности современного метода построения теории. Достаточно вспомнить, что из уравнений вытекали такие неожиданные предсказания, как вывод о существовании электромагнитного вакуума (состояния электромагнитного поля с наименьшей энергией, которое, несмотря на отсутствие фотонов, оказывает воздействие на поведение заряда, в частности электрона в атоме). Весьма необычными были предсказанные эффекты поляризации вакуума (эффекты, связанные с образованием электромагнитным полем виртуальных пар, которые вызывают в пространстве определенное распределение зарядов, наподобие поляризации диэлектрика, и оказывают на внешнее поле обратное воздействие, экранируя первичный заряд, создающий это поле).

Однако, отмечая эвристические функции метода математической гипотезы, мы не можем ограничиться только констатацией в общем-то тривиального факта, что в современной физике построение теории начинается с попыток “угадать” ее будущий математический аппарат.

Рефлексия исследователей, создававших новые теории, дает достаточно много высказываний такого типа[45]. Но это лишь первый шаг к осмыслению генезиса теории. Главная же задача состоит в том, чтобы за внешними признаками современного исследования увидеть логически необходимые операции, приводящие к построению новых систем теоретического знания. С этой точки зрения нам хотелось бы обратить внимание на два важных обстоятельства, относящихся к процессу становления квантовой электродинамики: 1) на обусловленность выдвигаемых математических гипотез предварительно принимаемой исследователями картиной физической реальности и 2) на корреляцию между процессом построения аппарата новой теории и процессом создания теоретической схемы, обеспечивающей интерпретацию указанного аппарата.