Построение развитой теории в классической науке

Введение теоретических схем в качестве гипотез с их последующим конструктивным обоснованием — главная познавательная процедура в генезисе теоретических знаний. Эта процедура определяет не только процесс становления частных теоретических схем, но и переход от них к развитой теории. В классической физике создание развитой теории начиналось обычно после того, как отдельные аспекты изучаемыхвзаимодействий отображались в некотором наборе частных теоретических схем и законов.

Первая фундаментальная развитая теория физики — ньютоновская механика — создавалась как обобщение теоретических моделей и законов таких видов механического движения, как колебание маятника, свободное падение тел, движение тел по наклонной плоскости, движение планет (законы Кеплера) и т. д. Аналогичная ситуация наблюдается в истории термодинамики и классической электродинамики, где отдельные аспекты изучаемых процессов были выражены в развитой сети частных теоретических схем и законов задолго до того, как были построены первые обобщающие теории этих разделов физики.

Развитая теория строится на основе синтеза частных теоретических схем. Они включаются в состав теории в трансформированном виде и предстают как выводимые (конструируемые) из ее фундаментальной теоретической схемы. Соответственно все частные теоретические законы выступают как следствие фундаментальных законов теории.

В этой связи возникает вопрос: каким путем создается ядро развитой теории — ее фундаментальная теоретическая схема и связанные с ней уравнения, выражающие основные законы теории.

Допустимы два предположения относительно способа формирования развитой теории. Можно допустить, что фундаментальная теоретическая схема и связанный с ней математический аппарат вводятся в качестве гипотез в уже развитой форме, а затем обосновываются теми частными теоретическими схемами и законами, которые теория должна включить в свой состав. Но возможно и иное предположение, согласно которому формирование фундамента развитой теории происходит постепенно, путем последовательного синтеза сначала некоторых близлежащих законов, обобщаемых в теории, а затем и законов, относящихся к более отдаленным областям исследуемых в теории взаимодействий.

История классической физики свидетельствует, скорее, в пользу второго предположения. Она показывает, что уже после построения ряда частных теоретических схем начинается процесс их экстраполяции на смежные областизнания с тем, чтобы унифицировать законы, описывающие определенную область взаимодействий, и объяснить все явления этой области с единой точки зрения. На этот счет можно привести достаточно много исторических примеров. Характерен вывод Галилеем законов колебания как особого случая закона движения по наклонной плоскости. Весьма показательна предпринятая Ампером попытка представить в качестве базисного закона электродинамики закон силового взаимодействия токов и вывести отсюда в качестве следствий закон Био—Савара и закон Кулона для магнитных полюсов.

Предполагая, что такого рода синтез является нормой построения теории, по крайней мере для этапа классической физики, определим центральный аспект этого синтеза .

Для развитой физической теории всегда характерна относительно высокая стадия математизации, и поэтому построение математического аппарата обычно считается ключевой задачей теоретического обобщения. Однако нельзя упускать из виду и вторую, не менее важную сторону, а именно связь математического формализма с теоретическими схемами, которые обеспечивают его интерпретацию. Отсюда при анализе исторического материала следует особое внимание обратить на связь между этими двумя аспектами познавательного движения (построением математического аппарата и построением его интерпретации).

Одной из опасностей, которая подстерегает философа и методолога при рассмотрении трудной и малоисследованной проблемы становления научной теории, является экстраполяция на любую разновидность теоретического синтеза выявленных современной наукой и распространенных в ней методов теоретического обобщения. Такая экстраполяция может быть осуществлена неосознанно, под влиянием сложившейся традиции, но она будет мешать обнаружению путей теоретического поиска, характерных для каждого этапа развития науки. В конечном итоге это может затруднить решение главной методологической задачи: установить, что меняется в приемах построения теоретических знаний в ходе эволюции физики и каковы инварианты исторически меняющихся форм познавательной деятельности, т. е. ее устойчивые и повторяющиеся черты, которые принадлежат к общим закономерностям теоретического исследования.

Чтобы избежать предвзятых мнений относительно методов построения развитой теории на том или ином этапе эволюции физики, следует обратиться к анализу реального исторического материала. Этот материал следует черпать не столько в учебниках по истории физики, задача которых дать сжатое описание основных этапов эволюции физики (эмпирических и теоретических открытий) и создать общую картину ее исторического развития, сколько в оригинальных текстах самих творцов научных теорий, текстах, запечатлевших результаты движения их творческой мысли. Такие тексты служат основнымэмпирическим базисом, на котором историк науки и методолог проверяют свои гипотезы.

С целью выяснить, как протекал процесс построения развитой теории в классической физике, рассмотрим один из важнейших фрагментов ее истории — становление максвелловской теории электромагнитного поля. Выбор этого фрагмента истории науки для логико-методологической реконструкции представляет особый интерес по следующим причинам. Во-первых, он интересен с точки зрения полноты “эмпирического материала”, крайне редкой для философского анализа истории науки (сохранились все основные тексты, фиксирующие принципиально важные этапы развития теории Максвелла, начиная с первых, эскизных вариантов и кончая ее относительно завершенной формой). Во-вторых, создание теории от начала и до конца было осуществлено здесь одним исследователем, в связи с чем можно выделять логически необходимые операции построения теории, без специальной временнóй реконструкции исторических фактов, поскольку в этом случае логика идей прослеживается в их реальной исторической последовательности. Поэтому на материале истории максвелловской электродинамики можно с достаточной полнотой проследить основные особенности выдвижения гипотез и их превращения в развитую научную теорию.

Анализ рассматриваемого исторического материала интересен еще и потому, что именно по отношению к максвелловской теории электромагнитного поля часто осуществляется некритический перенос современных методов исследования, которые в творчестве Максвелла в лучшем случае можно найти лишь в зародышевой форме. История максвелловской электродинамики чаще всего фигурирует в нашей литературе в качестве примера эффективности математической гипотезы при формировании аппарата развитой теории. При этом существует мнение, что фундаментальная идея тока смещения, приведшая к формулировке уравнений Максвелла, была обязана идеям симметрии.

Считается, что, записав в дифференциальной форме законы Кулона, Био—Савара, качественный закон Фарадея для электромагнитной индукции и выразив в уравнениях факт принципиальной замкнутости магнитных силовых линий, Максвелл обнаружил отсутствие симметрии в найденных уравнениях: а именно, что уравнение rot Е + 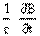= 0 (1) содержит производные как по координатам, так и по времени, тогда как в уравнение rot Н = 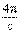J(2) входят только производные по координатам, а производные по времени отсутствуют.

Для восстановления симметрии Максвелл добавил в уравнение (2) новый член— производную от вектора электрической индукции (смещения) по времени 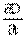, которая (будучи умноженной на — ) выступила в качестве математического выражения для тока смещения. Тем самым система уравнений электродинамики получила замкнутый характер и превратилась в математический аппарат теории. Из него естественно вытекало уравнение Даламбера для напряженностей электрического и магнитного полей, решение которого прямо приводило к предсказанию электромагнитных волн.

Такое представление на первый взгляд кажется вполне убедительным, если учесть простоту воспроизведенного хода рассуждений и его внешнюю очевидность (данные опыта, на которые мог опираться Максвелл, действительно не позволяли ему вывести идею о токе смещения и непосредственно ничего не говорили о существовании электромагнитных волн). Однако знакомство с реальным историческим материалом показывает, что процесс формирования максвелловской теории протекал иначе, чем это представляется в рамках традиционного понимания механизма математической гипотезы.

Попытаемся в сжатом виде проанализировать основные этапы этого процесса, акцентируя внимание на его внутренней логике.

Хорошо известно, что главная задача, которую решал Максвелл в период создания своей теории и которая была выдвинута всем предшествующим ходом развития науки, сводилась к поискам единого способа описания и объяснения различных аспектов электричества и магнетизма.

К этому времени отдельные стороны электромагнитных взаимодействий были достаточно хорошо изучены и отражены в целом наборе относительно самостоятельных систем теоретического знания. К ним относились теоретические модели и соответствующие законы электростатики (закон Кулона, закон Фарадея для электростатической индукции), магнитостатики и взаимодействия стационарных токов (закон Био Савара, закон Кулона для магнитных полюсов, закон Ампера), электромагнитной индукции (закон Фарадея), постоянного тока (законы Ома, Джоуля Ленца и т. д.) (рис. 4). Эти знания играли роль своеобразного эмпирического материала, на который опирался Максвелл при создании теории электромагнитного поля.

Основная проблема заключалась в сведении всей этой совокупности законов к некоторым обобщающим выражениям, из которых можно было бы выводить уже имеющиеся знания в качестве следствий. Для этой цели нужно было найти схему синтеза, которая бы обеспечила видение всего накопленного историей материала о природе электричества и магнетизма под единым углом зрения.

Рис. 4.

Такую синтезирующую схему задала предварительная картина электромагнитных взаимодействий, которая была принята Максвеллом и впоследствии развилась в электромагнитную картину мира, утвердившуюся в физике в конце XIX века. Эта картина вводила представление об электромагнетизме как передаче электрических и магнитных сил от точки к точке в соответствии с принципом близкодействия. Само выдвижение этой картины было подготовлено предшествующей историей науки ипрежде всего работами Фарадея.

Картина магнитных иэлектрических процессов, опирающаяся на принцип близкодействия, конкурировала с противоположной картиной физической реальности, которую в этот период истории электродинамики развивали Ампер и Вебер. Их теоретические исследования базировались на представлениях об электромагнитных взаимодействиях как о мгновенной передаче сил междуточечными зарядами и дифференциально-малыми элементами тока. На базе этого подхода, связанного с принципом дальнодействия, Ампер задолго до Максвелла предпринял попытку создать обобщающую теорию электричества и магнетизма. В целом он, а затем Вебер сумели развить достаточно богатую теорию, хотя последняя испытывала ряд трудностей, например при объяснении электромагнитной индукции.

Электродинамика Максвелла и электродинамика Ампера—Вебера длительное время конкурировали как две альтернативные исследовательские программы. Победа максвелловского направления была одержана только после построения теории электромагнитного поля и экспериментального обнаружения предсказанных теорией электромагнитных волн. Но в исходном пункте в период своего формирования программа Максвелла не имела никаких преимуществ перед соперничающим с ней направлением. Более того, электродинамика Ампера—Вебера уже была развита и к этому времени получила достаточно впечатляющие результаты. Поэтому сам выбор Максвеллом альтернативной картины электромагнитных процессов был достаточно смелым исследовательским шагом .

Если анализировать причины того, почему Максвелл осуществил этот шаг, то придется привлечь множество факторов, в том числе психологического и социокультурного характера. Но для логики научного познания важно, что такой шаг был подготовлен предшествующим развитием физики. И коль скоро речь идет о создании теории электромагнитного поля, то выдвижение картины физической реальности, основанной на идее близкодействия, было логически необходимым предварительным условием последующего построения указанной теории. Поэтому было необходимо, чтобы если не Максвелл, то какой-либо другой исследователь выдвинул бы данную картинув качестве основания новой программы перестройки электродинамики.

Фарадеевско-максвелловская картина физической реальности сразу же указала конкретные пути синтеза уже известныхзаконов электричества и магнетизма. Она определила область математических средств, с помощью которых можно было единым образом описывать самые разнородные электрические и магнитные явления. Эти средства, послужившие основой для построения аппарата будущей теории электромагнитного поля, заимствовались из механики сплошных сред, в частности из гидродинамики.

Сейчас хорошо известно, что именно за счет переноса математических структур из гидродинамики на область электромагнитных процессов Максвелл построил обобщающие уравнения электромагнитного поля. Но для того чтобы обратиться к этой области в самом начале исследования, Максвеллу нужно было заранее увидеть общее структурное сходство между весьма далеко отстоящими областями (механикой сплошных сред и электричеством и магнетизмом). Такое сходство обнаруживалось тлько благодаря принятой Максвеллом картине физической реальности. Для сравнения отметим, что вводимые Ампером и Вебером представления об электромагнитных процессах как взаимодействии точечных зарядов и токов путем мгновенной передачи сил требовали применения в электродинамики иных математических структур, заимствованных из ньютоновской механики материальных точек.

Различие в картинах физической реальности, лежащих в основании исследовательских программ Максвелла и Ампера—Вебера, обусловило иразличие в математических методах этих программ.

Перенос Максвеллом уравнений из гидродинамики на область электромагнитных явлений осуществлялся путем построения аналоговых моделей гидродинамического и квазимеханического типа (рис. 5).

Эта сторона вопроса достаточно хорошо освещена в историко-физической и философской литературе. Когда характеризуют процедуру создания математического аппарата максвелловской электродинамики, то использование аналоговых моделей плюс пробег в собственно математических средствах всегда описывают в качестве необходимого признака данной процедуры.

Внешне все выглядит так, как будто бы аппарат максвелловской теории был создан в результате непрерывного выдвижения все более совершенных уравнений, описывающих в обобщенной форме все новые аспекты электромагнетизма. Однако уже при более внимательном анализе выясняется, что у Максвелла “математический анализ сливается с физическим содержанием”[34], благодаря чему и оказывается возможным формирование теории электромагнетизма.

Лишь при поверхностном рассмотрении смена и трансформация аналоговых моделей, обеспечивающих развитие математических структур электродинамики, могут показаться логически недетерминированными, обусловленными лишь игрой научной фантазии исследователя.

В действительности же здесь был скрыт важнейший комплекс операций, необходимых для построения развитых теорий.

Выясняется, что аналоговые модели были не просто некоторым промежуточным звеном для трансляции математических средств. Внутри используемых аналогий Максвелл каждый раз выявлял конструктивное содержание за счет того, что систему связей и отношений между элементами аналоговой модели он представлял как изображение существенных черт экспериментально-измерительных ситуаций той предметной области, для описания которой предназначалось вводимое им уравнение. Именно эта процедура соединяла математическую форму с физическимсмыслом и позволяла обосновать каждое обобщающее уравнение в качестве описания законов электромагнитного взаимодействия.

Рис. 5.

Характерным примером в этом отношении может служить начальный пункт максвелловской работы.

Максвелл, приступая к реализации своей программы, вначале поставил задачу построить единую систему теоретического описания и объяснения электростатических явлений. Для этого необходимо было вывести единое обобщающее уравнение электростатики. Средством выведения такого уравнения послужила аналоговая гидродинамическая модель, основным элементом которой являлась единичная незамкнутая трубка тока некоторой идеальной несжимаемой жидкости. Эта модель позволила перебросить уравнение Эйлера для жидкости на область электростатических явлений и использовать его в качестве гипотетического выражения для обобщенного закона электростатики. Отсюда были получены в качестве следствий выражения для закона электростатической индукции и закона Кулона в дифференциальной форме[35].

Однако при всей привычности описанной ситуации возникает совершенно неясный с точки зрения логики момент: почему можно было интерпретировать гидродинамические уравнения в терминах электростатических величин? Ответ на этот вопрос дает сама процедура применения аналоговой модели. Оказывается, Максвелл обосновал ее как изображение существенных черт всех экспериментально-измерительных ситуаций электростатики, после чего само предположение о возможности истолковать гидродинамические величины уравнения Эйлера в терминах электростатики приобрело статус доказанной гипотезы.

В логически реконструированном виде процедура этого обоснования может быть описана следующим образом[36]. Вначале было установлено, что гидродинамическая аналогия изображает существенные черты явлений электростатической индукции. Уже в процессе переброски уравнений Эйлера на эту область трубка с несжимаемой жидкостью была уподоблена силовой линии, а набор таких трубок — характерномудля индукции изменению напряженности силовых линий в пространстве от точки к точке. Но тем самым Максвелл ввел, строго говоря, совершенно необычный объект — электрические силовые линии, существующие вне порождающих их зарядов. Такого объекта не было в предшествующих теоретических представлениях электростатики. В схеме электростатической индукции Фарадея силовые линии изображались как возникающие в идеализированном диэлектрике, ограниченном идеальными заряженными пластинами, и зависели от величины заряда на пластинах (модель идеализированного конденсатора). В максвелловской же модели они вводились по иному признаку. Поэтому требовалось специально доказать правомерность нового гипотетического свойства силовой линии. Доказательство было осуществлено по всем правилам конструктивного обоснования абстрактного объекта, который был выстроен в качестве объекта исследования, в системе процедур, представленных в модели электростатической индукции.

Мысленное варьирование зарядов на обкладке идеального конденсатора фарадеевской схемы и констатация того факта, что вместе с этим то убывает, то прибывает электрическая энергия в диэлектрике, позволили совершить предельный переход к случаю, когда вся электрическая энергия сосредоточена в диэлектрике. Это было эквивалентно представлению о наборе силовых линий, существующих тогда, когда устранены порождающие их заряды. Теперь картина силовых линий, оторванных от зарядов, оказалась идеализацией, восходящей к реальному экспериментальному материалу. Именно благодаря этому внутри аналоговой модели было выделено содержание, которое позволило представить ее в качестве выражения существенных черт взаимодействий, выявленных в экспериментальных ситуациях по изучению электростатической индукции.

Подобным же способом гидродинамическая модель трубок была обоснована Максвеллом и по отношению к ситуациям кулоновского взаимодействия зарядов.

Чтобы переписать на основе гидродинамических уравнений закон Кулона, Максвелл ввел изображение заряда как точечного источника (стока), из которого равномерно вытекает несжимаемая жидкость, поступающая в плотно прилегающие друг к другу трубки переменного сечения. Поскольку трубки с жидкостью были уже представлены как электрические силовые линии, постольку модель точечного источника стала изображением заряда, свойства которого характеризовались через признаки силовых линий. Тем самым было введено гипотетическое представление о заряде, который определен через напряженности создаваемого им поля.

Однако, если принять во внимание, что в модели Кулона заряд не содержал этой характеристики, а определялся через свойство “изменять состояние движения другого заряда”, то требовалось доказать эквивалентность обоих представлений. Только после этого можно было считать новое уравнение для зарядов равноценным закону Кулона.

Конструктивное обоснование гипотетического представления о заряде было легкоосуществимой операцией, если учесть возможность следующего мысленного эксперимента. В схеме кулоновского взаимодействия зарядов, которая сосредоточила в себе существенные черты соответствующих экспериментально-измерительных процедур электростатики, можно было варьировать величину зарядов. В предельном случае один заряд — “источник электрической силы” — можно было считать фиксированным, а другой заряд — сколь угодно малым. Тогда последний превращался в “пробный заряд”, который не оказывает на величину и направление электрической силы никакого воздействия, а позволяет лишь характеризовать плотность силовых линий, исходящих из порождающего их заряда. В результате заряд — источник поля — оказывается определенным только через характеристики поля так же хорошо, как и через свойство воздействовать на другой такой же заряд. Так внутри гидродинамической модели трубок было выявлено конструктивное содержание, относящееся к ситуациям кулоновского взаимодействия зарядов.

После всех описанных операций данная модель предстала уже как синтетическое изображение самых существенных черт экспериментально-измерительных ситуаций электростатики в целом. За ее внешней наглядной формой была скрыта теоретическая схема электростатики, которую можно было бы эксплицировать в виде отношения следующих абстрактных объектов: заряда, порождающего поле, пробного заряда и электрических силовых линий. Аккумулируя в себе основные и существенные черты всех экспериментов и измерений электростатики, данная теоретическая схема в силу этого представляла объект исследования отмеченной области. Она выступала как изображение структурных особенностей стационарного электрического поля. Такое видение теоретической схемы достигалось благодаря ее отображению на картину мира, принятую Максвеллом еще в начальном пункте теоретического исследования.

Соотнесение с картиной мира позволяло объективировать синтетическую модель электростатики. Силовые линии, отделенные от зарядов, приобрели тот же статус физической реальности, что и заряд. В свою очередь, такая онтологизация теоретических конструктов, оправданная их введением в качестве идеализаций, уходящих корнями в реальный эксперимент, формировала в физической картине мира новые представления, уточняя и развивая исходные образы электромагнитных взаимодействий. Физическая реальность “отделенных” от зарядов электрических силовых линий соответствовала представлению об электрическом поле, которое может быть рассмотрено как существующее в пространстве относительно независимо от его источников. Учитывая, что само существование такого поля могло быть оправдано только тем, что электрическая энергия сохраняется в поляризованном диэлектрике и при отсутствии зарядов, в картине мира должен был присутствовать (или появиться благодаря отображению на нее теоретической схемы электростатики) аналог идеального диэлектрика. Таким аналогом был эфир как среда, в которой могут существовать силовые линии. Заметим, что эфир, заполняющий пространство, был введен в развиваемой Максвеллом картине физической реальности по таким свойствам, которые как раз соответствовали свойствам идеального диэлектрика[37].

Таким образом, благодаря созданию обобщающей теоретической модели электростатики в обиход физического анализа были введены принципиально новые характеристики поля, которые были неизвестны до ее создания. Получив такой же статус физической реальности, что и заряд, электрическое поле в принципе могло предстать уже не только как порождаемое зарядом, но и как порождающее заряд (набор электрических силовых линий, стянутых в точку, мог рассматриваться как заряд).

Введенные Максвеллом обобщающие уравнения электростатики соотносились с новой системой физических понятий, благодаря чему получили обоснование в качестве выражений для законов стационарного электрического поля.

Эти уравнения выражали более глубокое физическое содержание, чем предшествующие им законы Кулона и Фарадея, превратившиеся теперь в частные случаи максвелловских уравнений для электрического поля.

Вся рассмотренная нами система теоретической деятельности Максвелла, связанная с выводом обобщенных законов электростатики, постоянно повторялась в процессе осуществляемого им грандиозного синтеза знаний об электричестве и магнетизме.

Гипотетически вводимые уравнения каждый раз обосновывались в качестве законов той или иной области электромагнетизма путем нахождения конструктивного смысла аналоговых моделей. Сами же эти процедуры протекали как операции с первичными теоретическими схемами электродинамики. В таких схемах отыскивалось инвариантное содержание, которое затем фиксировалось внутри каждой аналоговой модели. С этих позиций построение математического аппарата электродинамики Максвелла предстает уже не просто как серия математических экстраполяций. Оно оказывается связанным с процессом последовательного синтеза созданных в домаксвелловский период первичных теоретических моделей электромагнитного взаимодействия. Нетрудно увидеть в этом синтезе познавательное движение, направленное на создание обобщающей теоретической схемы, которая должна лечь в фундамент будущей теории и предстать как интерпретация ее аппарата. Именно в этом процессе постепенной кристаллизации фундаментальной теоретической схемы максвелловской электродинамики была заключена та внутренняя логика исследования, которая целенаправляла отбор аналоговых моделей. Последние же были не просто вспомогательными средствами, чем-то вроде строительных лесов, которые должны быть убраны, когда построено здание теории. Они служили особыми каркасами, часть которых становилась арматурой для возводимых стен теоретической постройки, входила в само “тело” создаваемой теории, а вторая, внешняя часть, связанная с наглядно-образной формой модели, оставалась лесами, которые облегчали создание теории и были устранены после ее создания.

В процессе становления математического аппарата теории электромагнитного поля движение в математических средствах постоянно корректировалось движением в сфере абстрактных объектов, образующих теоретические схемы электродинамики. Причем реальный исторический материал содержит прямые свидетельства неразрывности обоих типов познавательных операций.

В этом отношении чрезвычайно показательно, что, когда Максвеллу не удавалось выделить в аналоговой модели конструктивного содержания, сразу же приостанавливалось продвижение к математическому аппарату электродинамики.

Судя по всему, из поля зрения историков науки, даже тех, кто специально занимался анализом максвелловского открытия, выпадает следующий чрезвычайно важный факт. Оказывается, Максвелл, уже достаточно далеко продвинувшись в построении математического аппарата теории, столкнулся с непреодолимыми трудностями именно в том пункте, где, казалось бы, была найдена наиболее адекватная математическая форма законов электродинамики Это произошло на том этапе теоретического синтеза, когда был получен обобщенный закон электростатики div D = 4[38], введено уравнение rotH= 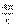J, обобщающее законы Ампера, Био—Савара и закон Кулона для магнитных полюсов[39], и, наконец, было предложено выражение Е = 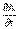, на базе которого Максвелл пытался получить математический закон электромагнитной индукции[40]. Последнее выражение Максвелл интерпретировал как связь между напряженностью электрического поля Е и так называемым “электротоническим вектором” А, который он ввел как характеристикупотенциальной возможности появления э.д.с. при изменении энергии магнитного поля. В современном понимании выражение Е = 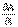соответствует определению поля Е через вектор-потенциал А. Если смотреть ретроспективно, то Максвелл, в сущности, уже“держал в руках” математическую схему электродинамики, причем в виде, весьма близко к ее современной формулировке (электромагнитные взаимодействия были представлены как отношение между электрическими, магнитными полями и токами; само же отношение “ток-поле” было задано в энергетической форме, посредством введения вектора-потенциала[41], что, как известно, соответствует современной, лагранжевой формулировке теории).

С позиций метода математической гипотезы Максвеллу оставалось сделать совсем немного: 1) взять ротор от обеих частей полученного равенства Е= 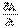и, учитывая введенное им ранее определение В=rot А (где В — вектор электромагнитной индукции), получить отсюда закон электромагнитной индукции в форме rot E= 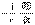;2) сопоставить последнее соотношение с полученным ранее уравнениемдля закона Био—Савара rot Н = 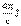; 3) обнаружить, что в уравнении rot Н = 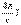для полной симметрии не хватает члена 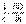, соответствующего току смещения.

Однако в действительности именно в этом пункте, казалось бы, наиболее перспективном с точки зрения традиционно приписываемого Максвеллу метода, сам он полностью отказался от дальнейшего развития полученного им формализма и, по существу, начал строить математический аппарат теории заново.

Этот факт, совершенно необъяснимый в рамках традиционных представлений о методах максвелловского исследования, легко может быть понят, если учесть связь между развитиемформализма теории и процедурами конструктивного обоснования теоретических схем.

Исторически Максвелл подошел к описанной выше формулировке законов электромагнетизма, опираясь на концепцию стационарных силовых линий.

Моделируя электрические силовые линии посредством представления о равномерном течении несжимаемой жидкости в незамкнутых трубках, Максвелл добился вначале обобщения знаний электростатики. Затем аналоговая “модель трубок” была экстраполирована на область магнитостатики и взаимодействия стационарных токов.

Учитывая вихревой характер магнитных сил, Максвелл видоизменил исходную аналогию и ввел представление о замкнутых трубках тока несжимаемой жидкости[42]. Посредством новой модели, выявляя в ней конструктивное содержание, он нашел обобщающий закон rot Н = 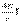, в котором фиксировалась связь между постояннымтоком и порождаемым им стационарным магнитным полем. Из этого закона были выведены в качестве частного случая выражения для законов Кулона, Био—Савара и Ампера.

Таким образом, в распоряжении создателя теории электромагнитного поля оказались два важных уравнения, одно из которых характеризовало постоянное электрическое, а другое — постоянное магнитное поле. Их связь он надеялся обнаружить в процессе поиска математического выражения для обобщенного закона электромагнитной индукции, посколькув явлении электромагнитной индукции явно прослеживалось взаимодействие электрических и магнитных сил.

Чтобы отыскать математический закон электромагнитной индукции, Максвелл использовал уже примененную ранее аналогию между циркуляцией несжимаемой жидкости в кольцевой трубке и стационарным магнитным полем, порождаемым магнитами н токами. Он перенес эту аналогию на новую область электромагнитных процессов, учитывая то обстоятельство, что в явлении электромагнитной индукции так же, как и в явлениях магнитного действия стационарных токов, прослеживалась генетическая –связь между электрическим током и магнетизмом. Посредством модели “кольцевой трудки” Максвелл попытался ассимилировать фарадеевские представления об электромагнитной индукции.

Однако именно здесь и возникли решающие трудности. Попытка выявить в аналоговой модели конструктивное содержание, соответствующее фарадеевским схемам индукции, приводила к утрате самого главного признака гидродинамической аналогии – ее способности моделировать магнитную силовую линию. Причина заключалась в том, что модель “кольцевой трубки” принципиально могла заместить и представить в познании только стационарную(постоянную во времени) магнитную силовую линию, тогда как для объяснения электромагнитной индукции существенно важно было учесть переменныйхарактер магнитного поля (изменение во времени потока магнитных силовых линий, пересекающих проводящее вещество). Именно поэтому в модели стационарно текущей в кольцевой трубке несжимаемой жидкости было невозможно представить существенные особенности электромагнитной индукции, не разрушая того содержания, которое выражало особенности процессов магнитостатики и взаимодействия стационарных токов. Несмотря на то, что посредством указанной модели были введены выражения Е = 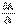и В =rot А, из которых легко можно было бы получить уравнение для электромагнитной индукции, отсутствие в аналоговой модели конструктивного содержания сразу же сказалось на свойствах вводимых уравнений. Их чисто формальные характеристики, как выяснилось позднее, были вполне пригодны для описания электромагнитной индукции. Однако был совершенно неясен физический смысл величин, которые фигурировали в уравнениях.

Максвелл попытался вначале интерпретировать их, вводя представления об изменении во времени энергии магнитного поля. Но тем самым он получил противоречивое определение поля, поскольку оно задавалось только как стационарное (поле изображалось как пространственная конфигурация стационарных силовых линий). Говорить же об изменении во времени энергии поля, которое с самого начала определялось как постоянное во времени, было бессмысленно.

В результате уравнения, введенные на базе аналоговой модели стационарно циркулирующей несжимаемой жидкости и предназначенные для описания электромагнитной индукции, оказались лишенными физического содержания. Они предстали в виде чисто математических формул, в которых один вектор определялся через другой, не имея иных, независимых определений. Поскольку в уравнения могло быть вложено физическое содержание лишь сугубо гипотетического характера, Максвелл вынужден был оставить этот сам по себе весьма перспективный формализм. Он просто-напросто не знал, как его применять для характеристики реальных измерений. Поэтому всю работу, связанную с построением единой теории электромагнетизма, исследователю пришлось проделать почти заново. Это был своего рода тупиковый этап максвелловского познавательного процесса. Но он подготовил переход к продуктивной стадии, завершившейся созданием теории электромагнитного поля.

Переход к этой стадии был связан с изменением стратегии теоретического поиска. Максвелл отказался от первоначальных попыток синтезировать знания об электромагнитных взаимодействиях на базе представлений о стационарных электрических и магнитных полях и обратился к идее нестационарных силовых линий. Под этим новым углом зрения он стал рассматривать прежний эмпирический материал.

Такая смена видения была результатом анализа трудностей, которые характеризовали непродуктивные попытки синтеза знаний магнитостатики и электромагнитной индукции. Сама тупиковая ситуация, возникшая на этом этапе, недвусмысленно показывала, что абстракция стационарной силовой линии является слишком грубой для того, чтобы построить обобщенную схему объяснения электромагнитных явлений. Поэтому необходимо было отыскать такое представление, из которого стационарная магнитная силовая линия “выводилась бы” как частный случай.

Представление данного типа Максвелл ввел с помощью известной модели вихря в несжимаемой жидкости[43].В этой модели вихрь репрезентировал магнитную силу в точке, набор же вихрей моделировал магнитную силовую линию. Внутри аналоговой модели Максвелл выявил конструктивное содержание, соответствующее обобщенной схеме магнитостатики ивзаимодействия стационарных токов, а из обобщающего уравнения, полученного на базе “модели вихря”, вывел как частный случай законы Ампера, Кулона и Био—Савара.

На первый взгляд может показаться, что Максвелл не получил ничего нового, поскольку уравнение, обобщающее законы Ампера, Кулона и Био—Савара, уже было получено им на предыдущих этапах теоретического синтеза. Однако, если обратить внимание на физический смысл такого уравнения, то ситуация предстает в ином свете. Раньше, записывая выражение для общих законов магнитостатики и взаимодействия стационарных токов, Максвелл принимал стационарное магнитное поле за основной объект, по отношению к которому переменное поле выступало в виде своего рода вырожденного случая. В новом же варианте, отказавшись от стационарной силовой линии как исходного объекта своих аналогий, Максвелл оборачивает отношения. Теперь уже стационарное магнитное поле может быть, в принципе, выражено через переменное[44].

В дальнейшем Максвелл произвел последовательный синтез знаний о постоянном токе и электромагнитной индукции, каждый раз модернизируя исходную аналоговую конструкцию (вначале к модели стационарного вихря был добавлен телесный элемент, изображающий движущийся заряд[45]; затем было введено представление о неравномерном вращении вихрей иускоренном движении связанных с ними телесных элементов, что моделировало взаимосвязь переменного магнитного поля и переменного тока).

В этом процессе вместе с исходной аналогией перестраивались в новую систему зависимостей соответствующие уравнения электромагнетизма. Показательно, что, получая такие уравнения в качестве гипотетических законов для все расширяющегося класса электромагнитных явлений, Максвелл обязательно доказывал правомерность вводимых теоретических представлений. Само же это доказательство всегда проводилось в двух планах. С одной стороны, из новых математических выражений для обобщенных законов каждый раз выводились все прежние известные законы как частный случай нового уравнения. С другой, каждая видоизмененная аналоговая модель обосновывалась Максвеллом в качестве изображения существенных черт всех тех экспериментальных ситуаций, которые подлежали теоретическому обобщению в рамках данной модели. Процедура такого обоснования осуществлялась путем конструктивного введения теоретических объектов электродинамики, представленных аналоговой моделью. Эти объекты вводились как идеализации на базе тех первичных теоретических схем, которые предполагалось синтезировать в рамках соответствующего аналогового образа. Причем после очередного изменения аналоговой модели Максвелл не только устанавливает, что в ней могут быть представлены существенные черты новой области взаимодействий, но и проверяет, не разрушилось ли при этом ее прежнее конструктивное содержание.

Показательно, например, что, ассимилировав “блок” знаний постоянного тока на базе модели вихря, Максвелл особым способом выводит из полученных обобщающих уравнений закон Био—Савара[46]. Вначале он мысленно выстраивает магнитное поле в виде конфигурации замкнутых силовых линий, а затем устанавливает, что оно соответствует току проводимости определенной величины. Этот эксперимент не может быть произведен в реальном опыте, но он понадобился Максвеллу, чтобы доказать, что введение в модель нового абстрактного объекта — тока, помеченного по “субстанциональным” свойствам (течь по проводнику, вызывать тепловое действие и т. д.), сохраняет прежний признак тока — “вызывать магнитное поле”.

Теоретический конструкт, который репрезентировал “субстанциональные” свойства тока, и конструкт, посредством которого характеризовалось магнитное действие тока, ранее были различными абстрактными объектами, посколькуобладали различными признаками.

Благодаря описанному мысленному эксперименту доказывались идентичность этих конструктов и возможность их замещения одним абстрактным объектом, который соединял отмеченные группы признаков. Тем самым устанавливалась непротиворечивость двух определений, образующих понятие “электрический ток”. Таким путем, в процессе построения все более полной ибогатой физическим содержанием теоретической схемы электромагнитных взаимодействий постепенно формировался понятийный каркас максвелловской электродинамики, который обеспечивал интерпретацию ее математического аппарата. В этомпроцессе происходило обогащение содержания ранее сложившихся понятий физики и вырабатывались новые понятия (например, переход к рассмотрению силовых линий в точке привел к появлению понятий “электрическая” и “магнитная” напряженности в точке). Причем в формировании понятийного аппарата максвелловской теории важную роль играли не только операции построения теоретической схемы путем идеализаций, опирающихся на реальные особенности экспериментов, но и процедура постоянного соотнесения такой схемы с физической картиной мира. Последнее приводило к уточнению наиболее общих представлений о структуре электромагнитных взаимодействий и обеспечивало развитие самых фундаментальных понятий электродинамики. Так, например, переход к анализу электрических и магнитных силовых линий, как “выстраивающихся” во времени от одной пространственной точки к другой, сформировал в физической картине мира представление об электрических и магнитных полях, распространяющихся в пространстве с конечной скоростью. Тем самым закладывался фундамент для последующей выработки основного понятия электродинамики — понятия электромагнитного поля.

Учет содержательно-физического аспекта познавательного движения Максвелла позволяет по-новому осмыслить многие особенности построения теории электромагнитного поля, в том числе и решающего ее этапа, связанного с выводом уравнения, включающего выражение для тока смещения. При таком подходе выясняется, что знаменитая идея тока смещения, завершившая формирование максвелловской теории, была введена вовсе не на путях математической гипотезы, а была получена значительно более прозаичным способом. Она возникла как результат построения аналогии, конструктивное содержание которой соответствовало обобщенной теоретической схеме всех известных Максвеллуобластей электромагнитного взаимодействия. На этой стороне проблемы следует остановиться несколько подробнее, поскольку речь идет о выводе одного из важнейших законов теории электромагнетизма, относительно метода получения которого имеются существенные неясности и разногласия .

Уравнение с током смещения было получено Максвеллом в связи с необходимостью учесть в уже созданных обобщающих законах особенности электростатических взаимодействий. До этого момента уже была построена система обобщающих уравнений для магнитостатики, тока проводимости и электромагнитной индукции. Аналоговой моделью, обеспечившей введение таких уравнений, послужило представление о вращающихся вихрях несжимаемой жидкости, между которыми расположены контактирующие с ними телесные элементы. В данной моделибыло выделено физическое содержание, которое соответствовало обобщающей теоретической схеме для магнитостатических процессов, явлений, связанных с током проводимости, и для электромагнитной индукции. Аналоговая модель выступала как символический образ всех этих процессов. В этой модели движение вихрей с постоянной скоростью сопоставлялось со стационарным магнитным полем, движение вихрей с ускорением — с переменным магнитным полем; телесный элемент — с дифференциально малой порцией электричества (заряда), перемещение телесного элемента — с током проводимости; тангенциальная сила, действующая на телесный элемент, соответствовала вектору электрической напряженности. Функционирование данной модели (рис. 6, а) выражало следующие особенности учтенных в ней процессов электромагнетизма: 1) возникновение тока проводимости под действием электрического тока (тангенциальная сила приводит в движение телесные элементы); 2) возникновение магнитного поля, порождаемого током (движение телесного элемента приводит во вращение вихри); 3) возникновение электродвижущей силы под действием переменного магнитного поля ипоявление индукционных токов (ускоренное вращение вихрей порождает тангенциальную силу, которая, в свою очередь, приводит в движение телесные элементы).

Максвеллу оставалось учесть только явления электростатики. Для этого он видоизменил исходную аналогию так, чтобы, сохраняя прежнее ее физическое содержание, отразить еще и специфику этой новой области взаимодействии. Он предположил, что вихри могут деформироваться, вызывая небольшое смещение телесного элемента. Такое смещение, в свою очередь, должно было изображать поляризацию зарядов при электростатической индукции.

Заменив для удобства вихри деформируемыми ячейками упругой среды, Максвелл затем доказал, что в новой модели представлены все существенные черты электростатических взаимодействий (доказательство проводилось на базе мысленных экспериментов с теоретическими схемами Фарадея и Кулона). После этого было произведено еще одно доказательство, устанавливающее, что в новой модели не утеряно и прежнее ее физическое содержание. Тем самым была создана теоретическая схема, обобщающая все известные Максвеллу знания об электричестве и магнетизме.

Из анализа данной схемы следовало, что ток смещения и ток проводимости вводятся по одному и тому же набору признаков, а значит, являются эквивалентными понятиями. Чтобы показать это, обратимся к рис. 6.

Рис. 6 а – вращающиеся вихри с₁ и с₂ приводят в движение элемент q и наоборот; б – телесный элемент, представляющий заряд, находится между способными к деформации, но не деформированными еще ячейками; в и г – деформация ячеек с₁ и с₂ соответствующая поляризации, и переход от деформированного состояния ячеек к недеформированному (снятие поляризации) приводит к перемещению элемента q

Представим себе начало поляризации диэлектрика с того момента, когда включается внешнее электрическое поле (см. рис. 6, б, в, г). В модели это изображается как появление силы, которая начинает “проталкивать” телесный элемент qмежду двумя ячейками с₁ и с₂. В процессе перемещения элементов между ячейками последние испытывают деформацию кручения, и возникающая при такой деформации упругая сила начинает противодействовать движению элемента qдо тех пор, пока она не уравновесит внешнюю силу. В этот момент происходит остановка телесного элемента в положении q₁, что соответствует установлению поляризованного состояния в рассматриваемом дифференциально малом объеме диэлектрика.

В ходе описанного взаимодействия телесного элемента с ячейками последние приходят во вращение с переменной скоростью, которая возникает в момент включения внешней силы (положение q₂) и вновь становится равной нулю в положении q₁. Поскольку вращение ячеек с переменной скоростью означает наличие нестационарного магнитного поля, постольку описанная картина возникновения поляризации соответствует эффекту порождения магнитного поля вследствие локального смещения зарядов в диэлектрике. С позиций динамической структуры модели было совершенно безразлично, является вращение ячеек результатом движения телесных элементов без деформации ячеек либо оно возникает как результат этой деформации. Это означало, что безразлично, является магнитное поле результатом локального смещения “элементов электричества” в процессе поляризации либо оно возникает как эффект тока проводимости. В любом варианте это было одно и то же поле. Но в таком случае смещение зарядов в процессе индукции согласно модели определялось уже по двум признакам: 1) “быть набором порций электричества, перемещающихся под действием электрического поля”; 2) “порождать магнитное поле”. Если учесть, что в ходе всех проведенных ранее процедур обоснования “ток проводимости” был введен как носитель этих же самых свойств, то Максвелл просто-таки не имел права проводить различие между ним и смещением зарядов в диэлектрике.

Он истолковал последнее как начало тока. В этом смысле отождествление “тока смещения” и“тока проводимости” было, скорее, логическим следствием движения в слое промежуточных интерпретаций, чем гениальной догадкой, внезапно осенившей создателя теории электромагнетизма.

Выразив все выявленные отношения элементов аналоговой модели на математическом языке, Максвелл получил свое знаменитое уравнение с током смещения: rot Н = 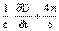J, которое замыкало систему уравнений электродинамики и явилось решающим этапом создания ее математического аппарата[47]. Здесь видно, насколько не соответствует историческим фактам представление о том, что Максвелл вывел это уравнение, пользуясь соображениями симметрии. Только относительно недавно в работе А.М.Борка[48] было указано, что эту симметрию уравнений Максвелла впервые зафиксировал О.Хевисайд лишь в 1885 г., а в текстах самого Максвелла полностью отсутствуют какие-либо свидетельства использования соображений симметрии. Солидаризуясь с выводом Борка, мы можем высказать более сильное утверждение: такого рода прием не мог быть использован Максвеллом в принципе, посколькуон не соответствует логике того реального познавательного движения, результатом которого явилась теория электромагнитного поля. Такие приемы построения теории стали типичными только в современную эпоху эволюции физики.

После создания системы максвелловских уравнений оставалось лишь выявить за строительными лесами аналоговых моделей созданное здание электродинамики. Весь этот процесс был закончен несколько позднее, но уже на заключительной стадии максвелловского синтеза полученная система уравнений и ее интерпретация сформировали новое видение электромагнитных процессов. Последние предстали как взаимодействие связанных между собой электрических и магнитных полей, распространяющихся в пространстве с конечной скоростью. Благодаря этому сама теория электромагнетизма должна была рассматриваться как описание существенных характеристик особой физической реальности — электромагнитного поля.

В заключение сформулируем некоторые выводы.

1. Анализ истории максвелловской электродинамики показывает, что при построении развитой теории исследователь может не обращаться непосредственно к экспериментальным данным, а использовать в качестве эмпирического материала теоретические знания предшествующего уровня (Максвелл нигде не оперирует непосредственно данными опыта, а учитывает их косвенно, оперируя с теоретическими схемами Фарадея, Кулона, Ампера и др.). В этом плане история электродинамики является одним из свидетельств того, что для построения новой теории не обязательно иметь новые эксперименты.

2. Одним из решающих пунктов создания максвелловской теории был предварительный выбор картины физической реальности, которая предопределяла характер применяемых математических средств и аналоговых моделей. Наличие картины физической реальности служит необходимым звеном теоретического синтеза, приводящего к основным уравнениям развитой физической теории. Указанная картина определяет программу теоретического синтеза, его стратегию.

3. Построение теории Максвелла протекало как процесс попеременного движения в математических средствах и плоскости физического содержания. Каждый новый шаг по пути к уравнениям электромагнитного поля сопровождался промежуточными интерпретациями, которые стимулировали новое движение в математических средствах. Такие переходы от математических средств к физическому содержанию и обратно происходили до тех пор, пока не завершился синтез всех знаний, обобщаемых в рамках максвелловской электродинамики. В качестве предположения, подлежащего проверке на конкретном историческом материале, можно сформулировать гипотезу, согласно которой, по-видимому, и в современной физике промежуточные интерпретации являются необходимым звеном построения теории.

4. Игнорирование связи между формально-математическими и содержательно-физическими операциями может привести к предвзятому истолкованию истории науки. В частности, неверно мнение, что Максвелл получил уравнение с током смещения, пользуясь соображениями симметрии. Это уравнение было получено на основе содержательно-физической модели.

Примечания

[1] Отметим, что эвристические функции картины мира в эмпирическом исследовании были зафиксированы и описаны мной еще в середине 70-х годов. Поэтому несколько казусным выглядит утверждение В.Н.Михайловского и Г.Н.Хона, что они впервые обращают внимание на то, что “картина мира как предзаданное видение позволяет изучать объекты, для которых еще не создано развитой теории. В этом случае и специальные (частные) картины мира и естественнонаучная картина мира целенаправляют исследования и активно участвуют в интерпретации получаемых результатов” (Михайловский В.Н., Хон Г.Н. Диалектика формирования современной научной картины мира. Л., 1989. С. 11—12). Если и говорить о приоритете в исследовании этих аспектов динамики знания, то он, бесспорно, принадлежит минской методологической школе (См.: Становление научной теории. С. 71—72; Природа научного познания. С. 163—173, 212—222; Идеалы и нормы научного исследования. С. 15).

[2] См.: Гильберт В. О магните, магнитных телах и о большом магните — Земле. М., 1956. С. 81—97.

[3] См.: Франкфурт И.У., Френк А.М. Христиан Гюйгенс. М., 1962. С. 192.

[4] Цит. по: Льоцци М. История физики. М., 1970. С. 291.

[5] Карпинская Р.С. Биология и мировоззрение. М., 1980. С. 184.

[6] См.: Горохов В.Г. Методологический анализ научно-технических дисциплин. М., 1984; Зеленков А.И., Водопьянов П.А. Динамика биосферы и социокультурные традиции. Минск, 1987; Петушкова Е.В. Отражение в живой природе. Динамика теоретических моделей. Минск, 1983; Шмаков В.С. Структура исторического знания и картина мира. Новосибирск, 1990; Шубас М.Л. Инженерное мышление и научно-технический прогресс: стиль мышления, картина мира, мировоззрение. Вильнюс, 1982; Смирнова Р.А. Природа социальной реальности. Минск, 1991 и др.

[7] Подробнее о структуре картин биологической реальности, предложенных Кювье и Ламарком, и функционировании их в качестве исследовательских программ см.: Кузнецова Л.Ф. Картина мира и ее функции в научном познании. С.91—94.

[8] Соловьев .И. Эволюция основных теоретических проблем химии. М.,1971. С.35—36.

[9] Там же. С.35.

[10] Последующее изложение преследует только одну цель — проиллюстрировать универсальность функционирования специальных научных картин мира в качестве исследовательских программ науки. Что же касается анализа структуры картин социальной реальности как особых компонентов социально-научного знания, их исторических типов, соотношения с конкретными социальными теориями — это задача особого исследования.

[11] Как следствие этих установок в марксистской исторической литературе преобладали описания экономического развития различных стран, революций и восстаний народных масс, но весьма редким исключением были работы, посвященные анализу глубинных менталитетов и ценностей, определяющих духовный климат той или иной исторической эпохи, исследования состояний массового сознания и образа жизни людей, характерного для этой эпохи и определенного вида общества.

[12] Лакатос И. История науки и ее реконструкции // Структура и развитие науки. М., 1978. С. 217.

[13] Резерфорд Э. Избранные научные труды. Строение aтомa и исскусственное превращение элементов. М., 1972. С. 223.

[14] Критический анализ модели Нагаока с этих позиций можно найти, например, в работах В.Вина (1905). (см.: Спасский Б И. История физики. Ч. II. М., 1977. С. 229.)

[15] Новые идеи в физике. Сб. 2. Эфир и материя. СПб., 1913. С. 13.

[16] Там же. С. 18—20.

[17] Там же. С. 23—27.

[18] Там же. С. 23—27.

[19] Интерес к проблемам строения вещества был вызван и влия­нием других факторов, например, успехов в развитии химии этого периода (здесь в первую очередь следует иметь в виду проблемы, к которым приводило открытие Менделеевым периодического закона). Но если бы внутри самой физики, в ее картине мира вопросы строе­ния вещества не были бы поставлены особенно остро, то, по-види­мому, это влияние осталось бы косвенным и не привело бы к той связи физико-химических исследований, направленных на изучение атома, которая наблюдалась с начала XX столетия.

[20] Максвелл Д.К. Избранные сочинения по теории электромагнитного поля. М., 1954. C. 372.

[21] Kuhn Т. Postscriptum-1969. In: Structure of Scientific Revolutions. 2 ed. enl. Chicago, 1970. С. 189—195.

[22] Ibid. P. 192—195

[23] Новые идеи в физике. Сб. 2. Эфир и материя. C. 18—21

[24] Льоцци И. История физики. М., 1970. С. 373—376.

[25] Льоцци И. История физики. С. 184—187.

[26] Неверно мнение, что Кулон получил свой закон из самих измерений без каких-либо предварительных теоретических предпосылок. У него была теоретическая гипотеза, которую он проверил в эксперименте.

[27] Маттис М. Теория магнетизма. М., 1967. С. 26.

[28] Теоретическое выражение для закона Кулона, сформулированного относительно идеальной ситуации взаимодействия точечных зарядов в пустоте, не следует путать с математической формулировкой эмпирической зависимости, которую Кулон получил из опытов с реальными наэлектризованными телами, взаимодействующими в реальной воздушной среде. Логически разный статус подобных выражений мы уже отмечали в гл. 1.

[29] См.: например. Рoрреr К. Logic der Forschung. Wien., 1935; Popper K. Conjectures and Refutations. N.Y.-L., 1963. P. 115—117.

[30] Все, что говорится в данном разделе о картинах мира, относится к классическому периоду развития физики. В современной физике эта ситуация воспроизводится в основных чертах, но с рядом существенных особенностей, о которых будет сказано ниже.

[31] Фарадей.Экспериментальные исследования по электричеству. Т. 1. М., 1947. С. 560.

[32] Там же. С. 25.

[33] Льоцци И. История физики. С. 276.

[34] Кузнецов Б.Г. Принципы классической физики. М., 1958. С. 289.

[35] Максвелл Д.К. Избранные сочинения по теории электромагнитного поля. М., 1954. С. 41—44.

[36] Попытка такой реконструкции впервые была предпринятаГ.Герцем (См.: Герц Г. Исследование по распространению электрической силы // Из предистории радио. М.-Л., 1948).

[37] В классической электродинамике доэйнштейновского периода эфир, с которым связывались все проявления электромагнетизма, наделялся свойствами диэлектрика. Это обстоятельство специально подчеркивал Л.И.Мандельштам в своих лекциях, посвященных физическим основам теории относительности (Мандельштам Л.И. Лекции по оптике, теории относительности и квантовой механике. М., 1972. С. 118, 135).

[38] Здесь и далее найденные Максвеллом выражения для законов электромагнетизма даются в современной форме их записи.

[39] Максвелл Д.К. Избранные сочинения по теории электромагнитного поля. М., 1954. С. 48.

[40] Там же. С. 78—80.

[41] Там же. С. 79—82.

[42] Там же. С. 45.

[43] Там же. С. 107—108.

[44] Там же.

[45] Там же. С. 132.

[46] Там же. С. 133—135.

[47] Там же. С. 169—170.

[48] См.: Максвелл Д.К. Статьи и речи. М., 1968. С. 315.

Глава V