Роль теоретических схем в дедуктивном развертывании теории

В логико-философском анализе языка науки довольно часто упускают из виду отмеченные особенности системной организации теоретических конструктов и не фиксируют теоретические схемы в качестве особых компонентов теории. На наш взгляд, это вызвано широко распространенным в логике и методологии науки подходом к любой научной теории только как к знанию, построенному по нормам аксиоматико-дедуктивной организации[12]. При рассмотрении научной теории с таких позиций видят в ней лишь выведение по правилам логики одних высказываний из других, что, в аспекте теоретического содержания, может быть истолковано как формирование все новых абстракций, призванных охарактеризовать исследуемую предметную область. Эти абстракции предстают как целостная система, внутри которой тем не менее весьма трудно выделить какие-либо уровни организации.

Однако естественнонаучные теории (впрочем, как и многие из теоретических систем математики), вообще говоря, лишь условно могут быть приняты за аксиоматико-дедуктивные системы. При анализе теоретических текстов обнаруживается, что даже в высокоразвитых теориях, широко использующих приемы формализованной аксиоматики, кроме формально-аксиоматической части существует некоторый принципиальный неформальный остаток, причем организованный вовсе не по нормам аксиоматико-дедуктивного построения.

Выясняется, что в процессе дедуктивного развертывания теории, наряду с аксиоматическими приемами рассуждения, большую роль играет генетически-конструктивный метод построения знаний, причем выступающий в форме своего содержательного варианта[13]. В отличие от аксиоматического метода, при котором “за исходное берут некоторую систему высказываний, описывающих некоторую область объектов, и систему логических действий над высказываниями”[14], генетический метод предполагает оперирование непосредственно с абстрактными объектами теории, зафиксированными в соответствующих знаках[15]. Процесс рассуждения в этом случае предстает “в форме мысленного эксперимента о предметах, которые взяты как конкретно наличные”[16].

Одним из примеров такого развертывания теории может служить евклидова геометрия[17]. Постулаты Евклида вводили основные абстрактные объекты — “точку”, “прямую”, “окружность”, “отрезок” — как определяемые через построение с помощью идеального циркуля и линейки. Все последующие рассуждения проводились на базе построения из основных объектов различных геометрических фигур. Мысленные эксперименты с фигурами (их расчленение и трансформация, а также их наложение друг на друга) служили основой для получения знаний, фиксируемых в системе соответствующих высказываний евклидовой геометрии[18].

Генетически-конструктивный подход сразу же делает очевидным факт существования теоретических схем. Такие схемы (вводимые в теоретическом языке в форме чертежей, снабженных соответствующими разъяснениями, либо через систему высказываний, характеризующих приемы конструирования и основные корреляции некоторого набора абстрактных объектов) предстают в качестве основы, обеспечивающей развертывание теоретических знаний.

Если с этих позиций рассмотреть процесс выведения из основных определений и аксиом физической теории их следствий, то обнаруживается, что, наряду с приемами развертывания знаний за счет движения в математическом формализме и формально-логических операций с терминами и высказываниями теории, большую роль играют мысленные эксперименты с абстрактными объектами теоретических схем. В этом нетрудно убедиться на любом конкретном примере. Так, возвращаясь к уже рассмотренному случаю с описанием процесса малых колебаний в рамках ньютоновской механики, можно установить, что выражение для закона малых колебаний нельзя получить из основных уравнений движения, если использовать только формально-логический вывод и средства математического формализма. Для вывода закона малых колебаний необходим целый ряд содержательных допущений: нужно конкретизировать вид силы, установить конкретный вид системы отсчета и рассмотреть характер перемещений материальной точки под действием квазиупругой силы в данной системе отсчета. Только после этого из основных уравнений движения механики можно вывести уравнение колебания. Все эти привычные для физика операции означают конструирование модели малых колебаний (осциллятора) на основе фундаментальной теоретической схемы механики и вывод уравнения колебания путем мысленного наблюдения за основными связями абстрактных объектов данной модели. В процессе такого вывода оперирование с элементами “осцилляторной модели” начинается с того момента, когда в уравнениях механики производится конкретизация вида силы, применительно к задаче малых колебаний. Уже само определение квазиупругой силы, как “силы, которая стремится возвратить материальную точку к положению равновесия”, эксплицирует осциллятор как модель малых колебаний. Только в рамках отношений между элементами этой модели может вводиться основной признак квазиупругой силы — “быть величиной, пропорциональной величине отклонения точки от положения равновесия”. Обозначая силу через F, отклонение от положения равновесия — через x получают выражение для силы F = -kx, где k — коэффициент пропорциональности. Подставляя это выражение в уравнение F=m 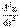получают уравнение малых колебаний m 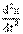+ kx = 0. Такова в деталях процедура вывода уравнения колебаний из основных законов механики. Наглядно ее можно изобразить посредством следующей схемы.

В рассуждениях физика осциллятор играет примерно ту же роль, что и геометрическая фигура в рассуждениях математика. Он позволяет установить связь между силой и величиной отклонения материальной точки от положения равновесия, что в свою очередь приводит к конкретизации второго закона Ньютона и превращению его в уравнение колебаний.

Даже при самом современном способе изложения физической теории с применением развитых математических средств нельзя избежать обращения к содержательным операциям с абстрактными объектами, входящими в теоретические схемы. Именно за счет таких операций накладываются ограничения на основные уравнения теории и формулируются частные законы, применимые к решению той или иной конкретной теоретической задачи. Так, в классической теории поля (достигшей в современном изложении весьма высокого уровня математизации) для того, чтобы получить, допустим, из фундаментальных уравнений электромагнитного поля (уравнений Максвелла) выражения для законов Кулона и Био—Савара, приходится предварительно произвести ряд мысленных экспериментов с фундаментальной теоретической схемой, которая характеризует посредством связи векторов электрического и магнитного поля и вектора плотности заряда-тока структуру электромагнитных взаимодействий.

Для вывода закона Кулона вначале конкретизируют фундаментальную теоретическую схему классической электродинамики и создают на ее основе теоретическую модель, которая характеризует электростатическое поле точечного источника. Предполагают, что поле создается точечным зарядом, т. е. что оно направлено по радиусу — вектору, проведенному из точки, в которой находится заряд е. Затем определяют поток электрического поля через шаровую поверхность с радиусом R вокруг заряда е. Соответственно этой модели трансформируют уравнения Максвелла. Вначале переписывают их в форме, соответствующей выражению законов для постоянного электрического поля, а затем применяют к конкретной ситуации расчета величины потока поля через шаровую поверхность. Только благодаря всем этим операциям на основе уравнений Максвелла получают их следствие — закон Кулона[19].

Аналогичным способом выводится и закон Био—Савара. Его нельзя получить путем одних математических преобразований уравнений Максвелла. Необходимо вначале трансформировать фундаментальную теоретическую схему классической электродинамики в ее “дочернюю” модель, характеризующую постоянное магнитное поле, порождаемое стационарным током. Поэтому вывод уравнения Био—Савара начинается с предположения, что заряды, создающие электромагнитное поле, совершают только “финитное движение, при котором частицы все время остаются в конечной области пространства, причем импульсы тоже остаются всегда конечными”[20]. Затем, опираясь на указанные конкретизирующие предпосылки, видоизменяют уравнение Максвелла

rot Н = 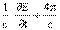J в уравнение rot = ,

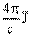после чего путем ряда математических преобразований[21] выводят закон Био—Савара, который в математической форме выражает корреляции абстрактных объектов теоретической схемы, характеризующей магнитное действие стационарного тока.

Таким образом, если заранее не подгонять любую естественнонаучную теорию под идеал аксиоматико-дедуктивного построения знаний, то можно довольно легко зафиксировать не только существование в ней теоретических схем, но и выявить важную роль последних в процессе развертывания теоретического содержания.

В физике такое развертывание может осуществляться, по меньшей мере, двумя взаимосвязанными способами:

а) путем формальных операций со знаками теоретического языка (например, операций с физическими величинами по правилам математики) и

б) за счет исследования методом мысленного эксперимента корреляций объектов, объединенных в теоретические схемы.

В первом случае не обращают внимания на смысл знаков[22]и оперируют с ними по некоторым заданным правилам, образующим синтаксис принятого теоретического языка. Во втором — обязательно эксплицируют содержание соответствующих знаковых выражений и вводят представление об абстрактных объектах, находящихся в строго определенных связях и отношениях друг к другу. Развертывание знаний осуществляется в этом случае путем мысленного экспериментирования с абстрактными объектами, исследование связей которых позволяет выявлять новые признаки абстрактных объектов и вводить новые абстракции, продвигаясь в плоскости теоретического содержания без обращения к приемам формализованного мышления. Показательно, что в развитой научной теории эти два способа выведения знаний дополняют друг друга. Во всяком случае, анализ процедур развертывания физической теории показывает, что пробег в сфере математики, которая задает приемы “формальной работы” с физическими величинами, всегда сочетается с продвижением в теоретических схемах, которые эксплицируются время от времени в форме особых модельных представлений.

Это, конечно, не значит, что при развертывании теории оперируют абстрактными объектами теоретических схем только тогда, когда прибегают к содержательно-генетическим приемам вывода. Движение в плоскости математического формализма также выступает как особый способ исследования свойств и отношений абстрактных объектов теоретической схемы. Поскольку такие свойства и отношения представлены в уравнениях в виде физических величин и их связей, постольку решение уравнений может быть рассмотрено как своеобразная процедура оперирования соответствующими абстрактными объектами теоретических схем. В этом понимании описание возможных способов решения уравнений правомерно расценивать как характеристику операций, которые могут быть проведены над абстрактными объектами.

Абстрактные объекты теоретической схемы могут эксплицироваться путем содержательных определений и содержательного описания их корреляций. Но вместе с тем они могут быть введены при развертывании теории путем замены части содержательных определений математическими выражениями и последующих операций с данными выражениями по правилам математики. Показательно, что связь содержательно-генетического и формального метода развертывания теории проявляется в постоянном переходе от одной формы “знакового бытия” теоретической схемы к другой[23]. В процессе вывода исследователь оперирует и математическим языком, и содержательными описаниями. Он время от времени корректирует движение в математическом формализме содержательными операциями с абстрактными объектами теоретических схем, а затем вновь переходит к формальному способу оперирования с данными объектами, исследуя их связи за счет преобразования знаков математического языка в соответствии с его нормами.

Поскольку развертывание физической теории обязательно предполагает редукцию фундаментальной теоретической схемы к частным, постольку возникает вопрос о способах и приемах такой редукции. При генетически-конструктивном методе построения теории необходимо не только определить исходные абстрактные объекты, но и задать способ построения на их основе новых абстрактных объектов. Процедуры такого построения обеспечивают переход от фундаментальной теоретической схемы к частным.

Специфика сложных форм теоретического знания, таких как физическая теория, состоит в том, что операции построения частных теоретических схем на основе объектов фундаментальной теоретической схемы не описываются в явном виде в постулатах и определениях теории. Эти операции демонстрируются на конкретных примерах редукции фундаментальной теоретической схемы к частной. Такие примеры включаются в состав теории в качестве своего рода эталонных ситуаций, показывающих, как осуществляется вывод следствий из основных уравнений теории. В механике к эталонным примерам указанного типа можно отнести вывод из законов Ньютона закона малых колебаний, закона движения тела в поле центральных сил, законов вращения твердого тела и т. д.; в классической электродинамике — вывод из уравнений Максвелла законов Био—Савара, Кулона, Ампера, Фарадея и т. п. Если проанализировать все эти формы вывода, то выяснится, что построение частной теоретической схемы на основе фундаментальной предполагает каждый раз обращение к исследуемому в теории объекту и выявление все новых его связей. При выводе с самого начала принимается во внимание специфика тех реальных процессов, для объяснения которых должна быть введена соответствующая частная теоретическая схема. Исследователь рассматривает эти процессы сквозь призму фундаментальной теоретической схемы (например, видит движение колеблющегося тела как перемещение материальной точки в системе отсчета), а затем осуществляет ряд мысленных экспериментов, в ходе которых налагает на фундаментальную теоретическую схему ограничения, соответствующие особенностям исследуемых процессов (например, отмечает, что процесс колебания связан с действием сил, которые каждый раз возвращают материальную точку в положение равновесия). За счет таких ограничений происходит конкретизация фундаментальной теоретической схемы, и она преобразуется в частную теоретическую схему.

Неформальный характер всех этих процедур, необходимость каждый раз обращаться к исследуемому объекту и учитывать его особенности при конструировании частных теоретических схем превращает вывод каждого очередного следствия из основных уравнений теории в особую теоретическую задачу. Дедуктивное развертывание теории осуществляется в форме решения таких задач. Решение некоторых из них с самого начала описывается в теории и предлагается в качестве образцов, в соответствии с которыми должны решаться все остальные задачи. Способ построения абстрактных объектов частной теоретической схемы на основе объектов фундаментальной теоретической схемы, необходимый для решения каждой новой теоретической задачи, демонстрируется на образцах уже решенных задач.

Отмеченную особенность дедуктивного развертывания физической теории зафиксировал Т.Кун при рассмотрении так называемых ординарных ситуаций научного исследования, связанных с приложением уже построенной теории к объяснению и предсказанию явлений.

Кун подчеркивал, что теоретическое описание и объяснение каждой новой физической ситуации осуществляется в соответствии с некоторой схемой видения (парадигмой), позволяющей изучать одну ситуацию по образу и подобию другой. В качестве главного компонента парадигмы он выделил образцы решения задач, благодаря которым осуществляется переход от основных законов теории к их следствиям, применяемым для характеристики тех или иных конкретных ситуаций[24].

Однако у Куна понятие образцов четко не определено. Лишь из контекста куновской работы можно установить, что он понимает под образцами способы оперирования модельными представлениями, которые обеспечивают вывод из одних формул математического аппарата других формул. В нашей терминологии эта деятельность может быть описана как редукция фундаментальной теоретической схемы к частной. Но последнее у Куна четко не выражено (в его работе вообще не дается характеристика структуры теоретических моделей и их типология). В этом смысле вышеизложенный анализ можно рассматривать как выяснение предметно-логической основы той деятельности, которую Кун называет использованием “образцов”.

Теоретические схемы и мысленные эксперименты с ними являются основой дедуктивного развертывания теории и ее приложения к описанию и объяснению различных проявлений изучаемой в теории реальности.

В свете сказанного можно внести ряд уточнений в представление о физической теории как о математическом аппарате, получившем физическую интерпретацию.

Во-первых, аппарат нельзя понимать как формальное исчисление, развертывающееся только в соответствии с правилами математического оперирования. Лишь отдельные фрагменты этого аппарата строятся подобным способом. “Сцепление” же их осуществляется за счет обращения к теоретическим схемам, которые эксплицируются в форме особых модельных представлений, что позволяет, проводя мысленные эксперименты над абстрактными объектами таких схем, корректировать преобразования уравнений принятого формализма.

Во-вторых, следует уточнить само понятие интерпретации. Известно, что интерпретация уравнений обеспечивается их связью с теоретической моделью, в объектах которой выполняются уравнения, и связью уравнений с опытом. Последний аспект называют эмпирической интерпретацией. Для обозначения первого аспекта нет устоявшегося термина. Иногда его называют семантической интерпретацией. Семантика уравнений определяется обоими аспектами интерпретации, причем эти аспекты связаны между собой (ниже будет показано, что построение эмпирической интерпретации предполагает отображение теоретической модели на объекты реального опыта).

Фундаментальные уравнения теории приобретают физический смысл и статус физических законов благодаря отображению на теоретическую схему. Но было бы большим упрощением считать, что таким образом обеспечивается физический смысл и теоретических следствий, выводимых из фундаментальных уравнений. Чтобы обеспечить такой смысл, нужно еще уметь конструировать на основе фундаментальной теоретической схемы частные теоретические схемы. Нетрудно, например, установить, что математические выражения для законов Ампера, Био—Савара и т. д., выведенные из уравнений Максвелла, уже не могут интерпретироваться посредством фундаментальной теоретической схемы электродинамики. Они содержат в себе специфические величины, смысл которых идентичен признакам абстрактных объектов соответствующих частных теоретических схем, в которых векторы электрической, магнитной напряженности и плотности тока в точке замещаются другими конструктами: плотностью тока в определенном объеме, напряженностями поля, взятыми по некоторой конечной пространственной области, и т. д.

Поскольку построение частных теоретических схем на основе фундаментальной предполагает использование эталонных ситуаций решения теоретических задач, постольку интерпретация математического аппарата развитой теории предполагает включение в теорию исходного набора таких ситуаций. Истоки их формирования и включения в теорию можно выяснить, только исследовав закономерности генезиса фундаментальной теоретической схемы.

Итак, фундаментальная теоретическая схема и ее производные образования представляют своего рода внутренний скелет теоретического знания, определяющий как содержательную специфику теории, так и процедуры ее развертывания. Учитывая это, по-видимому, не будет большим преувеличением сказать, что проблема генезиса теории прежде всего выступает как проблема становления ее теоретических схем. В пользу решающей роли таких схем в генезисе теоретических знаний говорит и то обстоятельство, что именно они обеспечивают особый статус необходимости, свойственный теоретическим законам и отличающий последние от эмпирических обобщений, представленных эмпирическими зависимостями.

В науке всегда можно найти такие разновидности эмпирических обобщений, которые выражаются в виде количественных зависимостей и по своей математической форме полностью совпадают с соответствующим выражением для теоретического закона. Хотя по внешнему виду такие выражения одинаковы, между ними существует огромное различие: первые обладают только вероятностной истинностью, вторые — представляют собой достоверное знание.

Качественно новый смысл эмпирической формулы, возникающий при переводе ее в ранг теоретического закона, обеспечивает ее соединение с теоретической схемой, т. е. обоснование ее в качестве математического выражения корреляций между абстрактными объектами, составляющими данную схему. В последнем нетрудно убедиться, разобрав любой конкретный пример отношения эмпирической формулы к теоретическому закону.

Допустим, что мы повторили опыты Р. Бойля и установили зависимость между объемом и давлением газа. Из табличных данных, полученных на базе реального эксперимента, можно вывести формулу pV = const, где p— давление, V— объем газа. Но сколько бы ни проводилось экспериментов с газами, никогда не будет гарантии, что в следующей серии опытов найденная зависимость не нарушится. Более того, она обязательно будет нарушаться, когда мы перейдем к опытам с большими давлениями, поскольку в этом случае существенную роль будут играть силы, которые не принимаются во внимание в законе Бойля—Мариотта, а учитываются лишь в уравнении Ван-дер-Ваальса. Это значит, что увеличение числа наблюдений не придает статуса необходимости разбираемой эмпирической зависимости. Для этого требуется особое доказательство, которое осуществляется следующим образом.

Вводится система абстрактных объектов, в качестве которых фигурируют: а) идеальный газ, представленный как набор идеально упругих и бесконечно малых частиц, соударяющихся друг с другом; в) идеальный сосуд, в который заключены эти частицы; с) идеальный поршень, который сжимает идеальный газ, двигаясь внутри сосуда. В процессе мысленного эксперимента устанавливаются следующие отношения данных объектов: идеально упругие частицы, двигаясь по законам механики, ударяются о стенки сосуда так, что суммарная сила всех их ударов на единицу площади характеризует давление газа. Математическое выражение этих отношений, основанное на применении фундаментальных законов механики, позволяет вывести зависимость pV = cоnst, зафиксированную ранее в опыте.

В результате этих процедур индуктивно полученная формула становится законом, описывающим поведение достаточно разряженных газов. Таким образом, для получения закона, характеризующего связь между объемом и давлением газа, понадобилось построить теоретическую схему, которая известна в науке как модель идеального газа. Эта модель фиксировалась в особой знаковой форме (например, в форме снабженного соответствующими разъяснениями чертежа, изображающего идеальный сосуд переменного объема и набор частиц газа, заключенных в сосуд). Затем при выражении связей и отношений между объектами данной схемы в математическом языке была получена формула pV=const, которая теперь предстала в качестве теоретического высказывания. Хотя ее вид остался тот же, что и при выражении на языке математики зависимости, полученной из опыта, величины р и V приобрели иной физический смысл. Они стали выражать уже не корреляции реальных, эмпирически фиксируемых сосудов и газов, а отношения абстрактных объектов теоретического языка, посредством которых строится модель идеального газа. В результате формула pV=const была возведена в ранг теоретического закона и приобрела признаки всеобщности и необходимости.

Рассмотренный пример принципиального различия между эмпирической зависимостью и теоретическим законом имеет корни в реальной истории науки. Он в сжатом виде воспроизводит логику открытия одного из основных законов теории газов. Сама история этого открытия весьма интересна и поучительна. Как эмпирическая зависимость формула pV=const была получена во многом случайно, как побочный результат спора между двумя известными физиками XVII столетия Р.Бойлем и Ф.Линнусом[25]. Спор шел по поводу интерпретации опытов Бойля, обнаруживших явление барометрического давления. Бойль проделал следующий опыт: трубку, запаянную сверху и наполненную ртутью, он погружал в чашку с ртутью. Согласно принципу сообщающихся сосудов следовало ожидать, что уровень ртути в трубке и в чашке будет выровнен. Но опыт показал, что лишь некоторая часть ртути выливается в чашку, а остальная часть в виде столбика стоит над поверхностью ртути в чашке. Бойль интерпретировал этот опыт следующим образом: давление воздуха на поверхность ртути в чашке удерживает столбик ртути над этой поверхностью. Высота столбика является показателем величины атмосферного давления. Тем самым был предложен принцип барометра — прибора, измеряющего давление.

Однако Ф.Линнус выдвинул следующие возражения: воздух состоит из легких частиц, он подобен тонкой и податливой жидкости, которая не может устоять под давлением тяжелых частиц ртути. Поэтому воздух не может удерживать столб ртути. Удерживает его притяжение ртути к верхнему концу барометрической трубки. Линнус писал, что, затыкая сверху барометрическую трубку пальцем, он чувствовал нити притяжения, когда опускал ее в чашку. Сам по себе этот исторический факт весьма показателен. Он свидетельствует о том, что один и тот же результат опыта может получить различные интерпретации и использоваться для подтверждения различных концепций.

Чтобы доказать Линнусу, что воздух способен удерживать столб ртути, Бойль поставил новый опыт. Он взял изогнутую в виде сифона стеклянную трубку с запаянным коротким коленом и стал постепенно наполнять ее ртутью. По мере увеличения столбика ртути воздух в колене сжимался, но не вытеснялся полностью. Бойль составил таблицу отношения объемов воздуха и величины столбика ртути и послал ее Линнусу как доказательство правильности своей интерпретации.

Казалось бы, история с объяснением барометрического давления закончена. Но она получила неожиданно продолжение. У Бойля был ученик, молодой человек по имени Тоунлей, которого Бойль обучал основам физики и математики. Именно Тоунлей, изучая таблицу опытов Бойля, подметил, что объемы сжимаемого воздуха пропорциональны высоте давящего на воздух столбика ртути. После этого Бойль увидел свои опыты в новом ракурсе. Столбик ртути — это своеобразный поршень, сжимающий воздух, и вес столбика соответствуют давлению. Поэтому пропорция в табличных данных означает зависимость между величиной давления и объема газа. Так было получено соотношение PV = const, которое Бойль подтвердил множеством опытов с давлениями, бóльшими и меньшими атмосферного.

Примерно в этот же период Мариотт повторил опыты Бойля, используя небольшие давления в экспериментах с различными газами и получил тот же результат.

Аппаратура, которой пользовались и Бойль, и Мариотт, не позволяла осуществить эксперименты с давлениями, значительно бóльшими атмосферного. Но если бы они имели возможности произвести такие эксперименты, то обнаружили бы нарушение открытой зависимости, и тогда никто не стал бы ее интерпретировать как закон.

Еще раз подчеркнем, что зависимость, открытая Бойлем, была вероятностно-истинным знанием, обобщением такого же типа, как утверждение “все лебеди белые”, которое было справедливым, пока не открыли черных лебедей. Теоретический же закон PV = const был получен позднее, когда была построена модель идеального газа.

Вывел этот закон физик Д.Бернулли (академик Санкт-Петербургской Императорской академии) в 1730 г. Он исходил из атомистических представлений о газе и представил частицы газа в качестве материальных точек, соударяющихся наподобие упругих шаров.

К идеальному газу, находящемуся в идеальном сосуде под давлением, Бернулли применил законы ньютоновской механики и путем расчетов получил формулу PV = const. Это была та же самая формула, которую уже ранее получил Р.Бойль. Но смысл ее был уже иной. У Бойля PV = const соотносилась со схемой реальных экспериментов и таблицами их результатов. У Бернулли она была связана с теоретической моделью идеального газа. В этой модели были выражены сущностные характеристики поведения любых газов при относительно небольших давлениях. И закон, непосредственно описывающий эти сущностные связи, выступал уже как достоверное, истинное знание.

Сказанному можно придать характер общего утверждения.

Поскольку предсказательная сила индуктивных обобщений всегда имеет только вероятностный характер, постольку простое расширение класса наблюдений, согласующихся с эмпирической зависимостью, не выводит ее из ранга гипотетического предположения о законе и не придает ей признака необходимости. Этот переход возможен лишь тогда, когда связь между величинами, представленными в эмпирической зависимости, будет получена в системе операций над абстрактными объектами теоретической схемы, которая является идеализированной моделью исследуемой реальности.

Таким образом, в качестве фундаментальной проблемы теории познания и методологии науки выдвигается проблема происхождения теоретических схем. На первый взгляд кажется очевидным, что источник их происхождения нужно искать в обобщении опыта, поскольку они создаются для описания уже известных данных опыта и предсказывания новых результатов. Задача состоит лишь в том, чтобы раскрыть, как осуществляется это обобщение.

Однако именно здесь и возникают основные трудности. К теоретическим схемам в первую очередь относится та характерная особенность возникновения теоретических знаний, которая заключается в невозможности вывести их из опыта чисто индуктивным путем.

Уже в простейшем случае с законом pV = cоnst видно, что используемая в процессе теоретического доказательства модель, в которой взаимодействие молекул газа представлено как соударение абсолютно упругих и бесконечно малых тел, не могла быть почерпнута непосредственно из опытов Бойля и Мариотта, хотя и была необходима для объяснения этих опытов. Еще более отчетливо эта особенность построения теоретических схем прослеживается в современной физике. Даже беглое знакомство с ее историей позволяет обнаружить специфику построения фундаментальных абстрактных объектов, образующих ее теоретические схемы. Нетрудно убедиться, что такие объекты, как, например, электронно-позитронное поле, энергия вакуума в квантовой электродинамике или четырехмерный пространственно-временнóй континуум в электродинамике Эйнштейна — Лоренца и т. п., первоначально вводились из теоретических соображений и лишь в дальнейшем получали эмпирическое обоснование. Но тогда перед теорией познания и методологией науки возникает задача объяснить, почему созданная таким способом система абстрактных объектов (теоретическая схема) может служить основой для предсказания данных опыта? Именно на этом пути нужно искать ключ к пониманию методов построения теории.

На наш взгляд, первые шаги в этом направлении должны быть связаны с анализом роли теоретических схем в рамках уже сложившихся знаний, когда последние используются для объяснения и предсказания реальных явлений. Поскольку в процессе объяснения и предсказания теоретические схемы соотносятся с изучаемой действительностью, постольку указанный анализ позволит выявить признаки, гарантирующие объективную ценность теоретических схем, что, в свою очередь, может послужить отправной базой для выяснения их генезиса.