Основные характеристики синусоидальных сигналов

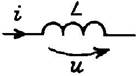
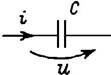
Синусоидальные токи и напряжения наиболее распространены из всех переменных во времени сигналов. Они легко генерируются в широком диапазоне частот, а их основные характеристики — амплитуду и частоту — удобно измерять и регистрировать. Расчет динамических режимов электрических цепей, находящихся под действием переменных источников e(t) и J(t), включающих емкости и индуктивности — динамические элементы, сложнее, чем анализ резистивных цепей. Общий подход к расчету, основанный на применении компонентных уравнений и уравнений Кирхгофа сохраняется. Однако уравнения цепи теперь будут дифференциальными, так как в них входят связи между токами и напряжениями на динамических элементах: uL = L di/dt; iC = C du/dt. Тем не менее, анализ синусоидальных режимов можно проводить на более простой математической основе, без составления и интегрирования дифференциальных уравнений. Результаты такого анализа могут служить базой для исследования цепей при воздействии сигналов более сложной формы, как периодических, так и непериодических.

Синусоидальный ток характеризуется амплитудой Im и периодом T (рис.1).

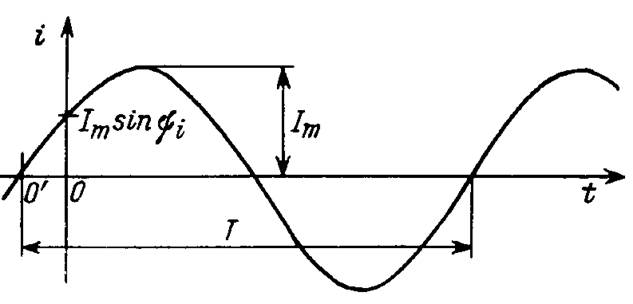
Рис. 1

При произвольном выборе начала отсчета времени его математическое выражение имеет вид i(t) = Im sin (wt + yi), где w — круговая (угловая) частота, w = 2pf (f — циклическая частота, определяющая число периодов колебаний за единицу времени), начальная фаза yi — аргумент синуса, отсчитываемый от ближайшей точки перехода через нуль 0' в положительном направлении. Аналогичны выражения для синусоидального напряжения u, ЭДС e, тока источника J:

u = Um sin (wt + yu); e = Em sin (wt + ye); J = Jm sin (wt + yj)

Энергетические характеристики синусоидальных сигналов обычно описываются действующими значениями тока I, равными среднеквадратичному за период значению:

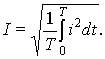
Аналогично вводятся действующие значения напряжения U и напряжения ЭДС E. Действующие значения наиболее часто используют для характеристики интенсивности синусоидальных сигналов: электроизмерительные приборы проградуированы так, что они показывают действующие значения синусоидальных токов и напряжений. Для синусоидальных величин вычисление интеграла в последнем выражении приводит к соотношениям:

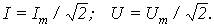
Приведенное общее выражения действующего значения справедливо также и для периодических сигналов, отличных по форме от синусоидальных.

В линейной цепи, находящейся достаточно долго под действием синусоидальных источников одной частоты f с неизменными амплитудами, токи и напряжения на всех участках будут иметь также синусоидальную форму с той же частотой, так как при протекании по катушке синусоидального тока iL(t) напряжение на ней uL = L di/dt также синусоидально, поскольку синусоидальные функции сохраняют свою форму при дифференцировании. Аналогично связаны напряжение и ток конденсатора. При суммировании синусоидальных токов и напряжений на отдельных участках цепи в уравнениях Кирхгофа их форма также не изменяется.

Поэтому анализ синусоидального режима в цепи сводится к определению амплитуд и начальных фаз отдельных токов и напряжений, которым отвечают частные решения дифференциальных уравнений, описывающих процесс. Их можно найти, даже не составляя эти дифференциальные уравнения.

Токи и напряжения на различных участках цепи имеют различные начальные фазы — компонентные соотношения для индуктивности и емкости выражают то, что токи и напряжения на них не совпадают по фазе. Поэтому при анализе цепи возникает необходимость суммирования сигналов с различными начальными фазами.

Разность фаз двух синусоидальных сигналов одной частоты y1 – y2 = 0 называется их фазовым сдвигом. При y1 > y2 (q > 0) говорят, что ток i1 опережает по фазе ток i2 (рис. 2, б), и наоборот, i2 отстает по фазе от тока i1. При q = 0 сигналы совпадают по фазе, одновременно достигая максимума и переходя через нуль. Два сигнала с q = p находятся в противофазе, сигналы с q = ± p/2 находятся в квадратуре

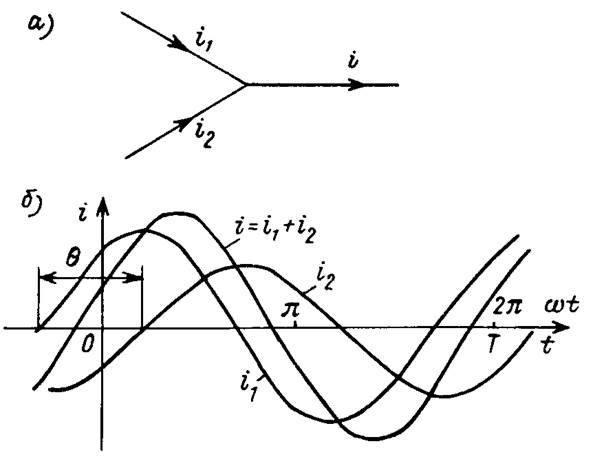
Рис. 2

Если сходящиеся в узле (рис. 2, а) синусоидальные токи имеют фазовый сдвиг i1(t) = Im1 sin (wt + y1), i2(t) = Im2 sin (wt + y2), то для их суммы i(t) = Im sin (wt + y) = i1(t) + i2(t) нахождение амплитуды Im и начальной фазы y по временным зависимостям громоздко (рис. 2, б).

В цепях синусоидального тока уравнения Кирхгофа нельзя применять к амплитудам (или действующим значениям) токов и напряжений, не совпадающих по фазе. Алгебраическое суммирование токов и напряжений в соответствии с законами Кирхгофа возможно лишь для мгновенных значений i или u.

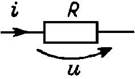
1. Связи между синусоидальными напряжениями и токами в активном сопротивлении, в индуктивности, в емкости.

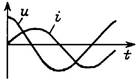
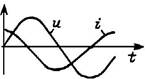
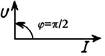
Используя компонентные уравнения, установим связь между основными характеристиками тока и напряжения на элементах. Подставив мгновенные значения тока i = Im sin wt в компонентные уравнения для uR и uL и напряжения u = Um sin wt — в iC, получим выражения для uR, uL и iC, приведенные в Таблице 7.1, из которых следуют соотношения между амплитудами и действующими величинами напряжений и токов U и I. Отношение U/I = Um/Im представляет сопротивление элемента — активное R и реактивные — XL (индуктивное) и XC (емкостное). Размерность всех сопротивлений — Ом. Обратные величины I/U представляют проводимости элементов — активную G и реактивные: BL (индуктивную) и BC (емкостную). Значения реактивных сопротивлений (и проводимостей) зависят от частоты. Выражения для мгновенных токов и напряжений i и u показывают, что ток и напряжение на резисторе совпадают по фазе, на индуктивности ток отстает от напряжения на угол p/2, а на емкости ток опережает напряжение на p/2.

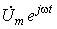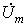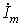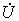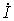Переход к комплексным характеристикам элементов осуществляется с помощью комплексных изображений мгновенного тока для сопротивления и индуктивности и напряжения для емкости. Подстановка их в компонентные уравнения приводит к комплексным изображениям uR, uL и iC, приведенным в Табл. 1, из которых получаем соотношения комплексных амплитуд напряжений и токов элементов и действующих значений и . Они выражают закон Ома в комплексной форме, в которой выступают комплексные сопротивления элементов 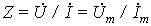. Обратные им величины — это комплексные проводимости 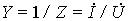. Комплексный характер сопротивлений и проводимостей Z и Y отражает информацию о фазовых сдвигах токов и напряжений на элементах.

Таблица 1.

Связи между синусоидальными напряжениями и токами на элементах R, L, C

Характеристика	Связи между напряжениями и токами на элементах
Во временной области
Компонентное уравнение	u = Ri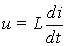
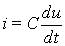
Мгновенные значения тока и напряжения	i = Im sin wt;   uR = RIm sin wt	i = Im sin wt;   uL = wLIm cos wt =   = wLIm sin (wt + p/2)	u = Um sin wt;   iC = wCUm cos wt =   = wCUm sin (wt + p/2)
Амплитуда	Um = RIm	Um = wLIm	Um = (1/wC)Im
Действующие ток и напряжение	U = RI	U = wLI	U = (1/wC)I
Сопротивление   Проводимость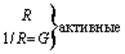
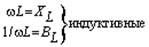
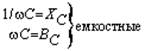
Начальная фаза тока и напряжения	yu = yi	yu = yi + p/2	yu = yi – p/2
Угол сдвига фаз между током и напряжением j = yu – yi		p/2	– p/2
Графики тока и напряжения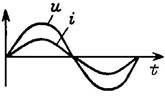
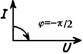
Векторная диаграмма

2. Входные и передаточные функции цепей синусоидального тока

Применение комплексного метода сводит соотношения между мгновенными токами i(t) и напряжениями u(t), выражаемые дифференциальными уравнениями, к алгебраическим соотношениям между их комплексными изображениями I(jw), U(jw). Поэтому составленные для цепи уравнения в комплексной форме позволяют алгебраически выразить любой комплексный ток или напряжение – выходную величину 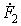через входную величину 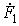— напряжение или ток, подаваемые к входным зажимам:

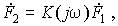
где K(jw) — передаточная функция цепи, являющаяся рациональной дробью аргумента jw, коэффициенты полиномов числителя и знаменателя которой выражаются через параметры цепи. Передаточная функция является комплексным числом

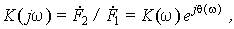
модуль которого K(w) выражает отношение действующих значений (или амплитуд) выходного и входного сигналов, а ее аргумент q(w) определяет фазовый сдвиг между ними:

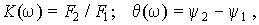
где y2 и y1 — начальные фазы обоих сигналов.

Размерность передаточной функции определяется размерностями связываемых ею величин. Если входная и выходная величины — напряжения (рис. 3, а), то передаточная функция K(jw) безразмерна; то же относится и к случаю, если обе величины являются токами (рис. 3, б). Если выходная величина — напряжение, а входная — ток (рис. 3, в), то говорят о передаточном сопротивлении Z12(jw) и наконец, соотношение между входным напряжением и выходным током определяет передаточная проводимость Y12(jw) (рис. 3, г).

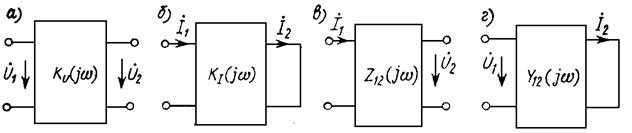
Рис. 3.

Входные величины — комплексное сопротивление двухполюсника (рис. 4) 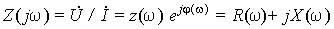и входная проводимость 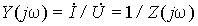также выражаются рациональными дробями аргумента jw.

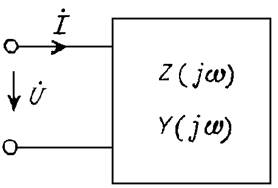
Рис. 4.

Модулем комплексного входного сопротивления является полное сопротивление цепи Z(w), его аргументом j(w) — фазовый сдвиг между напряжением и током, вещественная часть R(w) — активное, а мнимая часть X(w) — реактивное сопротивление.

Для комплексной входной проводимости аналогично имеем

Y(jw) = y(w) e-jj(w) = G(w) - jB(w),

где y(w), G(w) и B(w) — полная, активная и реактивная проводимости цепи.

Определим входные и передаточные функции для цепи (рис. 5).

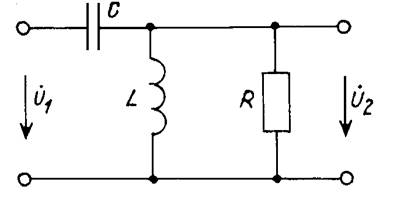
Рис. 5.

Выражая комплексные сопротивления ветвей

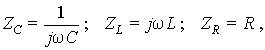
запишем входное сопротивление цепи:

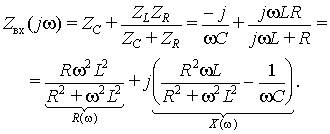
Вещественная часть входного сопротивления пассивной цепи неотрицательна:

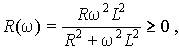
а его мнимая часть может быть как положительной, так и отрицательной

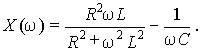
Получим выражение для передаточной функции рассматриваемой цепи по напряжению:

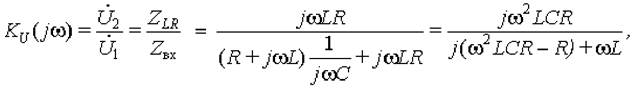где ZLR = jwLR/(jwL + R) (при переходе к последнему выражению числитель и знаменатель дроби были умножены на wC).

Передаточная комплексная функция имеет модуль

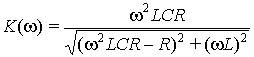
и аргумент

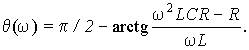
Амплитудные и фазные частотные характеристики. При анализе процессов преобразования сигналов электрическими цепями представляет интерес исследование зависимостей передаточных и входных функций рассматриваемой цепи от частоты. График частотной зависимости модуля передаточной функции называется амплитудно-частотной характеристикой, а график зависимости аргумента передаточной функции — фазочастотной характеристикой. Обе зависимости, построенные в широком частотном диапазоне, дают наглядное преобразование о характере преобразования сигналов данной цепью.

На рис. 6 по приведенным выше зависимостям построены частотные характеристики цепи рис.5.

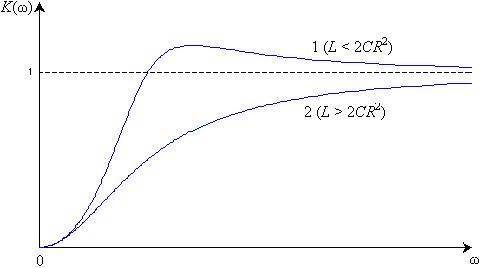
Рис. 6

Из них следует, что эта цепь пропускает преимущественно сигналы высоких частот. В зависимости от соотношения ее амплитудно-частотная характеристика имеет максимум (кривая 1), либо монотонно увеличивается от нулевого значения при w = 0 до K(w) = 1 при w ® ¥. Оба эти предельных режима легко проанализировать. При w = 0 (режим постоянного тока) конфигурация цепи упрощается, так как постоянный ток не протекает через конденсаторы, а индуктивности представляют для него нулевое сопротивление. Поэтому для определения передаточной функции на постоянном токе конденсаторы в схеме следует разомкнуть, а катушки — закоротить. Получим чисто резистивную цепь, анализ которой существенно проще. Аналогично при w ® ¥ сопротивления конденсаторов цепи стремятся к нулю, а сопротивления катушек неограниченно возрастают. Поэтому для анализа цепи при высоких частотах следует, наоборот, закоротить конденсаторы и разомкнуть катушки, что опять сводит задачу к расчету чисто резистивной цепи.

Применим сформулированные правила к анализу асимптотических режимов при w ® 0 и w ® ¥ в рассматриваемой цепи.

Существуют и другие способы представления частотных свойств передаточных функций: путем изображения частотных характеристик вещественной и мнимой частей K(jw) = Kв(w) + jKм(w) либо с помощью построения на комплексной плоскости кривой, которая отвечает совокупности значений K(jw), соответствующих различным частотам — амплитудно-фазовая частотная характеристика.

На рис. 7. изображена амплитудно-фазовая частотная характеристика передаточной функции цепи (рис. 8.3).

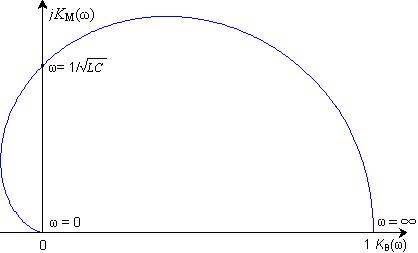
Рис. 7

Для ее построения при отдельных значениях частоты находят вещественную и мнимую части передаточной функции: Kв(w) = K(w) cos q; Kм(w) = K(w) sin q. Эти значения соединяют на комплексной плоскости непрерывной кривой, которая наглядно позволяет проследить характер изменения K(jw) при изменении w от нуля до бесконечности.

Аналогично изображают и частотные характеристики входных функций: сопротивления Z(jw) = R(w) + jX(w) = z(w)e jj(w) — его вещественной и мнимой частей R(w) и X(w), модуля z(w) и фазового сдвига j(w) или проводимости Y(jw).