Структурные уравнения электрических цепей.

Структура электрической цепи накладывает ограничения на распределение токов и напряжений на отдельных ее элементах. При расчете цепи информация о структуре отражается в структурных уравнениях, выражающих первый и второй законы Кирхгофа, которые определяют:

1) баланс токов в сечениях цепи — ;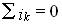

2) баланс напряжений в контурах — .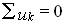

Входящие в эти уравнения величины суммируются алгебраически — токи ветвей сечения, направления отсчета которых совпадают с ориентацией сечения, положительны, а не совпадающие с ней — отрицательны. Также и напряжения, направление отсчета которых совпадают с направлением обхода контура, берутся со знаком “плюс”, а противоположные ему — “минус”.

Первый закон Кирхгофа часто применяют к сечениям, охватывающим один узел. Он формулируется как равенство нулю всех токов, сходящихся в узле цепи. Второй закон Кирхгофа записывают с заменой напряжений на источниках значениями ЭДС этих источников:

Su_k = Se_k.

Такая формулировка определяет равенство алгебраической суммы падений напряжения на остальных элементах контура сумме ЭДС источников, действующих в этом контуре. При этом со знаком “плюс” в обеих частях равенства учитывают величины, совпадающие с направлением обхода контура.

Использование уравнений Кирхгофа для расчета цепи требует формирования независимой системы уравнений. Наиболее простой путь заключается в записи уравнений первого закона Кирхгофа для всех узлов цепи, кроме одного (любого). В связной цепи с q узлами он приводит к q – 1 независимому уравнению. Другая возможность состоит в использовании главных сечений, каждое из которых включает лишь одну из ветвей дерева цепи. Так как дерево содержит q – 1 ветвь, система независимых уравнений первого закона Кирхгофа, записанная для главных сечений, включает также q – 1 уравнение. Независимость этих уравнений определяется тем, что в каждом из них содержится один ток, не входящий в другие уравнения — ток ветви дерева.

При записи уравнений второго закона Кирхгофа при выборе независимых контуров в планарной цепи (все ветви которой можно изобразить на плоскости без перекрещиваний) проще всего использовать элементарные ячейки, образованные ветвями цепи. Так, для мостовой цепи, граф которой изображен на рис. 1.8, б, такой путь приводит к контурам и ƒ. В общем случае в качестве независимой системы используются главные контуры, каждый из которых содержит только одну из ветвей связи.

2. Формирование системы уравнений электрической цепи. Законы Кирхгофа.

Система уравнений, позволяющая решать задачу анализа цепи, включает компонентные и структурные уравнения.

Компонентные уравнения выражают соотношения меду токами и напряжениями на отдельных ветвях цепи. Сюда относятся закон Ома и соответствующие соотношения для индуктивностей и емкостей, связи токов и ЭДС управляемых источников с управляемыми величинами.

При описании цепи в качестве ветвей можно рассматривать не только перечисленные идеализированные элементы. Для получения более компактной системы уравнений отдельные двухполюсные фрагменты цепи, включающие несколько элементов, представим как составные ветви. Это целесообразно в том случае, когда распределение токов и напряжений внутри такого фрагмента не представляет интереса.

Компонентные уравнения составных ветвей можно получить суммированием напряжений и токов на участках рассматриваемого фрагмента. Для первых двух составных ветвей (рис. 1, а,б) они имеют одинаковую форму u = Ri – RJ – e или тождественную ей: i = G(u + e) + J (G = 1/R). Составная ветвь (рис. 2.1, в) описывается компонентным уравнением i = (G1 + G2 + G3)u + G1e1 + G2e2 + G3e3.

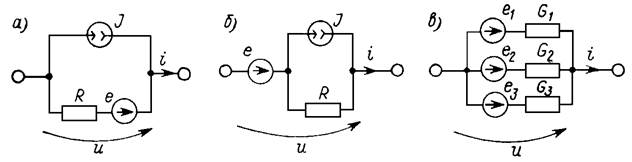
Рис. 1

При изображении графа цепи вся составная ветвь заменяется одной дугой, т. е. информация о ее внутренней структуре в граф не входит.

Из приведенных компонентных уравнений линейных резистивных цепей без управляемых источников, изображенных на рис. 1, следует, что для невырожденных составных ветвей эти уравнения могут быть записаны в общей форме u(i) или i(u):

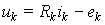или

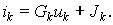
Однако компонентные уравнения ветвей, состоящих из идеальных источников ЭДС и тока, содержат информацию лишь об одной из величин — u или i. Такие ветви называются вырожденными.

Как было указано, независимой является система, составленная по первому закону Кирхгофа для всех узлов цепи, кроме одного, и система контуров — элементарных ячеек планарной цепи для записи уравнений второго закона. В общем случае для получения независимой системы следует выбрать дерево цепи и составить уравнения первого закона для главных сечений выбранного дерева и уравнения второго закона для его главных контуров.

Для цепи с n ветвями и q узлами при отсутствии вырожденных ветвей, состоящих из идеальных источников, система уравнений электрической цепи содержит n компонентных уравнений, q – 1 уравнение первого закона Кирхгофа и n – q + 1 уравнение второго закона. Полученная система таким образом 2n уравнений определяет n неизвестных токов и n напряжений.

3. Узловые уравнения

Недостатком метода расчета, основанного на непосредственном решении уравнений электрической цепи, является необходимость оперировать с большим числом уравнений. Число неизвестных в такой системе легко сократить, исключая с помощью компонентных уравнений либо токи, либо напряжения ветвей, т. е. выбирая в качестве базиса одну из переменных для каждой ветви. Однако и это приводит к необходимости решать систему уравнений, число которых равно числу ветвей.

Часто в виде подобного базиса используют узловые напряжения — напряжения узлов цепи относительно одного узла, принятого в качестве опорного. Для связной цепи с q узлами число таких напряжений равно q – 1. Основой для формирования узловых уравнений являются уравнения первого закона Кирхгофа.

Для вывода узлового уравнения рассмотрим k-й узел цепи (рис. 2), соединенный с узлами 0, 1 – 3 ветвями, содержащими проводимости G = 1/R, источники ЭДС и тока.

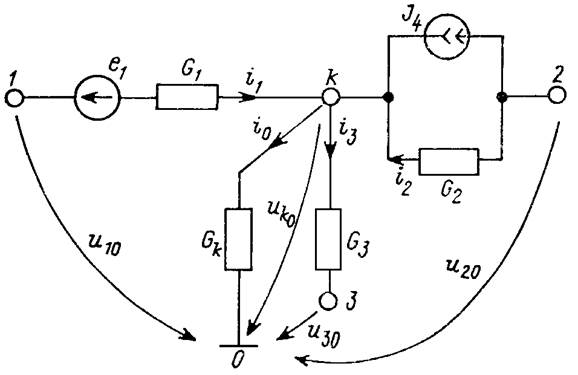
Рис. 2

При выборе направлений токов, указанных на рис. 2, уравнение первого закона Кирхгофа для k-го узла имеет вид

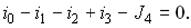
Выразим токи в ветвях, присоединенных к узлу, через узловые напряжения u₁₀, u₂₀, u₃₀ и проводимости ветвей G:

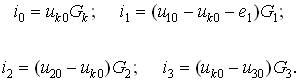
Подстановка и группировка членов приводят уравнение первого закона к виду

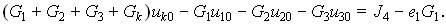
В общем виде узловое уравнение для k-го узла можно записать, используя двойную индексацию проводимостей, принятую для линейных алгебраических систем:

G_k1u₁₀ + G_k2u₂₀ + ...+ G_kku_k0 + ... = J_kу.

Как следует из рассмотренного примера, коэффициент G_kk — собственная проводимость k-го узла — равен сумме проводимостей всех ветвей, присоединенных к данному узлу. Коэффициент G_km — общая проводимость узлов k и m — представляет взятую со знаком “минус” сумму проводимостей ветвей, соединяющих непосредственно узлы k и m. Правая часть узлового уравнения — узловой ток J_kу — равен алгебраической сумме источников тока, присоединенных к данному узлу. Источники ЭДС e в составных ветвях, включенные последовательно с проводимостями G, учитываются в узловых токах в виде произведения eG рассматриваемой составной ветви (пока предполагается отсутствие ветвей с идеальными источниками ЭДС, для которых G = ¥). Слагаемые узлового тока берутся со знаком “плюс” для источников, направленных к данному узлу, и со знаком “минус” — при противоположном направлении.

Таким образом, для цепи с q узлами имеем q – 1 узловое уравнение с q – 1 неизвестными — линейную алгебраическую систему, общая матричная запись которой имеет вид

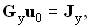
где G_у — квадратная матрица узловых проводимостей; u₀ — вектор узловых напряжений; J_у — вектор узловых токов:

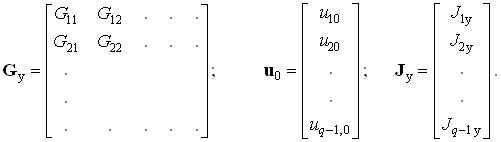
Матрица узловых проводимостей пассивной цепи является симметричной — общие проводимости равны друг другу G_mk = G_km по смыслу их определения.

3.1 Формирование узловых уравнений пассивных цепей

При формировании узловых уравнений следует пронумеровать узлы анализируемой цепи. В качестве опорного узла с индексом "0", относительно которого отсчитываются все остальные напряжения, целесообразно принять узел, к которому присоединяется наибольшее число ветвей или заземленный узел цепи.

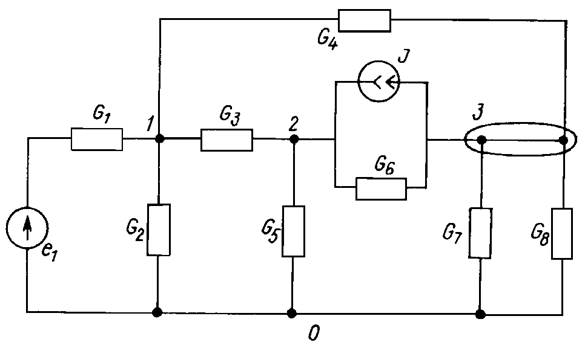
Рис.3

Принятая на рис. 3 нумерация узлов приводит к следующим выражениям собственных и общих проводимостей узлов:

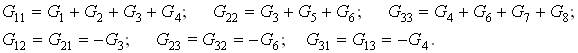
Узловые токи равны: J_1у = e₁G₁; J_2у = J; J_3у = – J.

Полученные выражения подставляем в систему уравнений:

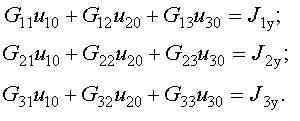
3.2 Формирование узловых уравнений для цепей с идеальными источниками ЭДС

Если к узлу присоединены вырожденные ветви с идеальными источниками ЭДС, обладающими нулевым внутренним сопротивлением, узловое уравнение для такого узла теряет смысл, так как при нулевом сопротивлении проводимость ветви равна бесконечности.

Однако, если один из узлов, к которым подключен независимый идеальный источник ЭДС e (рис. 4, а) выбрать в качестве опорного (0), то значение узлового напряжения второго узла 1 будет известным, так как оно непосредственно определяется величиной источника: u10 = e.

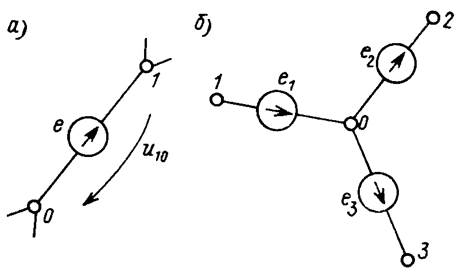
Рис.4

Таким образом, потеря одного из узловых уравнений, составленных по обычным правилам, не препятствует решению, так как соответственно сокращается и число неизвестных узловых напряжений.

Аналогично поступаем и при действии в цепи нескольких идеальных источников, имеющих общие узлы (рис. 4, б). При выборе в качестве общего узла (0) напряжения узлов 1 – 3 определяют величинами ЭДС, подключенных к этим узлам: u10 = – e1; u20 = e2; u30 = e3. Очевидно, что в рассматриваемом случае в качестве опорного узла может быть выбран любой из узлов (1, 2 или 3). При этом напряжения остальных узлов определяют алгебраическим суммированием ЭДС идеальных источников. В результате для расчета цепи методом узловых напряжений получаем систему меньшей размерности.

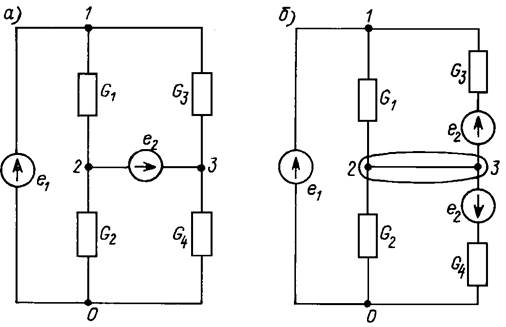
Рис.5

Другой способ, применяемый при отсутствии общего узла у действующих в цепи идеальных источников ЭДС (рис. 5, а), состоит в переносе одного из идеальных источников (например, e2) через узел 3 и включение его в резистивные ветви G3 и G4 (рис. 5, б).

Действительно, обе цепи, изображенные на рис. рис. 3.5, а,б, эквивалентны друг другу, так как при переносе ЭДС через узел для преобразованной цепи сохраняются все соотношения, вытекающие из второго закона Кирхгофа. После выполненного преобразования для объединенного узла 2 и 3 составляют общее уравнение по обычному правилу формирования узловых уравнений.

Таким образом, наличие идеальных источников ЭДС не только не усложняет применение метода, но и приводит к сокращению числа искомых узловых уравнений.

4 Контурные уравнения

Метод контурных токов использует в качестве базисной системы переменных, через которые выражаются токи и напряжения цепи, контурные токи, замыкающиеся в независимых контурах цепи. При этом соотношения, базирующиеся на уравнениях первого закона Кирхгофа, и компонентные уравнения используют для исключения напряжений из уравнений второго закона Кирхгофа. Это приводит к системе контурных уравнений, неизвестными в которых являются токи, циркулирующие в независимых контурах. Поэтому число неизвестных в системе равно числу независимых контуров цепи. Как и в методе узловых напряжений, описанная процедура исключения при решении задач не выполняется, а контурные уравнения составляются непосредственно. Рассмотрим один из независимых контуров цепи (рис. 6).

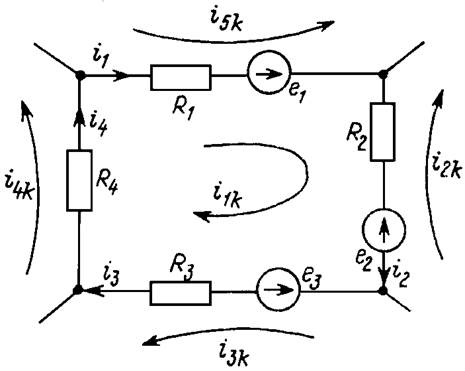
Рис. 6

Принимая в качестве положительных направлений токов в ветвях указанные на рис. 6, запишем уравнение второго закона Кирхгофа

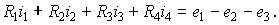
Считая, что в рассматриваемом и смежных с ним контурах циркулируют контурные токи iк, выразим через них токи в ветвях

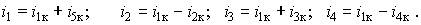
Подставляя эти выражения в предыдущее уравнение, получим контурное уравнение

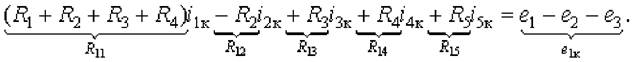
Коэффициент R₁₁ при контурном токе i_1к называется собственным сопротивлением контура; он образуется суммированием сопротивлений всех ветвей, входящих в данный контур. Коэффициент уравнения R_km, имеющий различные индексы, — это общее сопротивление контуров k и m, равное сумме сопротивлений общих ветвей обоих контуров. Знак этой суммы определяется относительным направлением контурных токов в общих ветвях. Если оба контурных тока протекают по этим ветвям в одном направлении, то сопротивление R_km имеет знак “плюс”, при противоположном направлении обоих контурных токов — знак “минус”. При отсутствии общих ветвей контуров R_km = 0. Правая часть уравнения — контурная ЭДС e_к — равна алгебраической сумме ЭДС источников в данном контуре. Знаки этих ЭДС определяются правилом их учета в уравнении второго закона Кирхгофа: совпадающие с направлением контурного тока ЭДС берутся со знаком “плюс”, противоположные ему — со знаком “минус”. В матричной форме система контурных уравнений цепи имеет вид:

R_кi_к =e_к,

где R_к — матрица контурных сопротивлений; iк — вектор-столбец контурных токов; e_к — вектор-столбец контурных ЭДС;

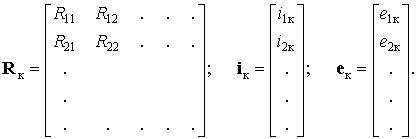
Матрица контурных сопротивлений симметричная (R_km = R_mk) и имеет размер p*p (p — число независимых контуров цепи).

Полученная система сходна с системой узловых уравнений: диагональные элементы обеих матриц R_к и G_у формируются по принципу принадлежности к данному узлу или контуру, сходны и правила формирования недиагональных элементов матриц — общих для двух узлов или контуров. Здесь, однако, аналогия не является полной, так как общие проводимости G_km узловой матрицы пассивной цепи всегда имеют знак “минус”, а общие сопротивления контурной матрицы могут иметь различные знаки.

1. Методы эквивалентных преобразований

Метод преобразований основан на последовательном упрощении структуры цепи путем сокращения числа ее узлов и контуров.

Простейшие преобразования включают замену последовательно соединенных ветвей с сопротивлениями R_k одной ветвью с эквивалентным сопротивлением R_э = SR_k и параллельных ветвей с проводимостями G_k эквивалентной ветвью с проводимостью G_э = SG_k.

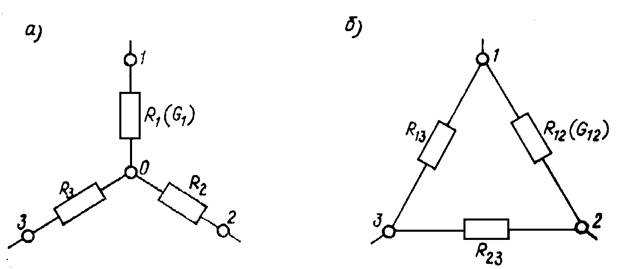
Рис.7

Преобразования звезды (рис. 7, а) в эквивалентный треугольник (рис. 7, б) и наоборот определяются формулами для сопротивлений

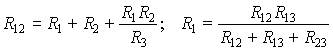
или тождественными формулами для проводимостей

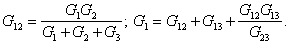
Соотношения для остальных параметров аналогичны приведенным и получаются посредством круговой перестановки индексов 1 – 3.

Последовательное применение преобразований упрощает структуру, и цепь приводится к простейшему виду, содержащему лишь последовательное или параллельное соединение элементов.

При преобразовании ветвей с источниками ЭДС и тока используют взаимные преобразования этих источников), а также перенос идеальных источников ЭДС через узел. Последовательно включенные источники ЭДС e_k алгебраически суммируются: e_э = Se_k, параллельно включенные источники тока могут быть заменены эквивалентным источником J_э = SJ_k. Все перечисленные виды преобразований источников справедливы и для управляемых источников.

При преобразовании цепей с управляемыми источниками иногда целесообразно применять преобразование управляющих величин. Так, если управляющее напряжение и представляет падение напряжения на резисторе с сопротивлением R, то в качестве управляющей величины можно использовать ток резистора i, выражая управляющее напряжение как u = R_i и подставляя эту связь в соотношение для ЭДС или тока управляемого источника. Аналогично можно осуществить обратную замену управляющего тока i, протекающего через резистор с проводимостью G, на управляющее напряжение, используя связь i = G_u, которую подставляют в выражение ЭДС или тока источника.

Однако изменение характера управляющей величины требует более сложных преобразований, если управляющее напряжение определяется как сумма напряжений на различных участках цепи или управляющий ток является током вырожденной ветви с нулевым сопротивлением.