Моделирование происшествий с помощью сетевых диаграмм
Основные принципы моделирования сетей такие же, как и моделирование графов. Отличительной особенностью моделирования сетей является возможность учета динамики протекания процесса во времени, а также случайного характера возникновения предпосылок. Поэтому в таких сетях вводятся дополнительные узлы и дуги, образующие обратные связи и учитывающие ограничения и условия реализации процессов. При этом они могут не иметь тождественного физического отображения. Кроме того, сетевые модели позволяют учитывать параллельно протекающие процессы в системах. При моделировании происшествий с помощью сетей применяются как аналитические, так и имитационные модели. Распространение получили сети GFRT и сети Петри.
В качестве основных параметров, характеризующих элементы сети GFRT, используются:
a) затраты времени, средств и других ресурсов: tij
б) вероятности осуществления связей: Рij
в) функции плотности вероятности распределения ресурсов или функция принадлежности, характеризующая закон распределения: fij или pij (mij)
г) условные производящие функции моментов вероятностного распределения Мij(S)
Производящими функциями моментов называют некоторые аналитические зависимости, последовательное взятие производных от которых дает выражение для начальных моментов порядка S.
Mij(s)= 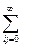
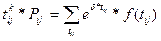
k – порядковый номер начального момента;
tij – дискретная случайная величина.
Для постоянной величины tij формула упрощается:
Mij(s)=esa
Таким образом, начальные моменты могут быть найдены дифференцированием производящей функции и приравниванием данного параметра к нулю полученной производной.
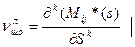 s=0
s=0
Использование производящих функций моментов упрощает количественный анализ процессов, описываемых как сетями GFRT, так и другими видами диаграмм влияния за счет совмещения двух параметров.
Wij=Pij*Mij(s) – пропускная способность отдельной дуги или всей сети.
Для определения вероятности наступления события всей сети и оценки числовых характеристик М, D проводят упрощение исходной модели сети с помощью правил упрощения, аналогичных для модели графа.
Примечание: Эти правила преобразования справедливы только для случайных замкнутых стохастических сетей, для которых существует обратная связь между стоком и истоком сети.
Производящие функции моментов для различных законов распределений
| № | Распределение | Производящая функция М(S) |
| Биномиальное | (P*es+1-e)n | |
| Дискретное | 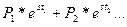 /P1+P2+…+Pn /P1+P2+…+Pn
| |
| Экспоненциальное (показательное) | 1/(1-S/a) | |
| Геометрическое | P*es/(1-es+P*es) | |
| Нормальное (Гаусса) | Exp(s*m+0,5*s2* 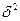 ) )
| |
| Пуассона | Exp( 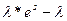 ) )
| |
| Равномерное | (esd-es 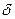 )/(a- )/(a- 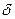 )s )s
|
a, b, m, n, l, s, t – параметры распределения.
Приведем пример сети GFRT:
 |

| |
| |




| |
 W34
W34




| |

 W12
W12






| |
| |

| |
 W23
W23
| | | ||||||
 | |||||||
 | |||||||
| |
| |
| |

 W35 1
W35 1


| |
| |
| |

 W22
W22
 WA(S)
WA(S)
Для упрощенного анализа проводят идентификацию сети по правилу упрощения с использованием топологического уравнения Мэсона.
1 – 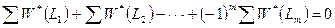
где 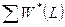 – сумма коэффициентов пропускания i-го порядка
– сумма коэффициентов пропускания i-го порядка
Введя искусственную обратную связь с коэффициентом пропускания 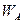 можно записать
можно записать
1 – 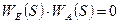
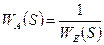
В приведенной сети существуют три обратные связи:
1) 
2) 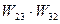
3) 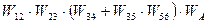
Все эти петли являются петлями I порядка по определению. Подставляя в топологическое уравнение получаем:
1 – 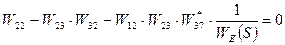
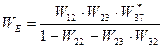
Предположим, что сеть моделирует появление потенциально опасной ситуации при выполнении следующих операций технологических процессов:
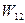 – контроль исходного состояния оборудования;
– контроль исходного состояния оборудования;
 – устранение возможных отклонений;
– устранение возможных отклонений;
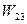 – выполнение адаптивных действий;
– выполнение адаптивных действий;
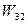 – подготовка к следующему действию при благоприятном результате операции;
– подготовка к следующему действию при благоприятном результате операции;
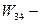 возникновение опасной ошибки;
возникновение опасной ошибки;
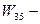 появление отказов элементов техники;
появление отказов элементов техники;
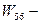 вывод из строя средств защиты при отказе техники.
вывод из строя средств защиты при отказе техники.
| ij | Pij | Распределение | Параметры | Mij(S) |
| 0,9 0,1 0,8 0,1 | const нормальное нормальное const экспоненциальное | a=1
m=3; 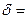 2
m=10; 2
m=10; 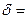 3
a=2
a=100
a=1000
a=1000 3
a=2
a=100
a=1000
a=1000
| esa exp(3s+0,5*4*s2) exp(10s+0,5*9*s2) e2s 1/(1-100s) |
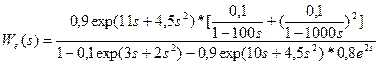
Искомая вероятность возникновения происшествия получается из соотношения
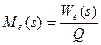
Подставляем значение Q в выражение эквивалентной производящей функции момента
Из этого выражения можно определить моменты любых порядков для получения количественных значений параметров происшествия М[Т] – математическое ожидание времени до возникновения аварийной ситуации.
M[T]=  =2502c
=2502c
D[T]= 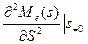 =11656c
=11656c
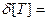 107,96c
107,96c
M[T] 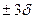 [T]=(42
[T]=(42 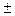 5,5)мин
5,5)мин
Дата добавления: 2016-04-02; просмотров: 1060;
