Магнитные цепи с переменными магнитными потоками: общие сведения.
В реальных цепях переменного тока помимо обычных элементов - сопротивлений, индуктивностей и ёмкостей часто встречаются и элементы с ферромагнитными сердечниками - катушки с сердечниками. Особенность цепей переменного тока с ферромагнитными элементами заключается в том, что переменные токи в обмотках и магнитные потоки в сердечниках взаимосвязаны. С одной стороны, магнитные потоки зависят от токов в обмотках, и при анализе цепей приходится в значительной мере пользоваться методами, разработанными для магнитных цепей с постоянными магнитными потоками. С другой стороны, токи в обмотках зависят от характера изменения магнитных потоков, и это весьма усложняет исследования. Учитывая эти особенности, на практике вводят различные допущения и упрощения. Например, иногда считают связь между индукцией и напряженностью магнитного поля линейной, но учитывают потери энергии в сердечниках. Иногда - наоборот, пренебрегают потерями в сердечниках, но связь между индукцией и напряженностью считают нелинейной.
В цепях с ферромагнитными элементами нельзя считать индуктивность и взаимную индуктивность постоянными, и приходится использовать непосредственную зависимость между ЭДС и магнитным потоком или потокосцеплением.
В основе индукционного действия магнитного поля лежит закон электромагнитной индукции (закон Фарадея-Максвелла). Согласно этому закону в контуре, движущемся в неизменном поле так, что его стороны
пересекают магнитные линии, или в контуре, помещенном в изменяющееся во времени магнитное поле, индуктируется ЭДС, численно равная скорости изменения во времени магнитного потока, пронизывающего этот контур:
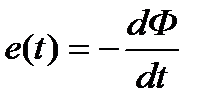
|
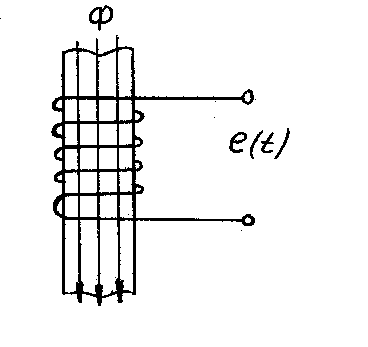
Когда контур состоит из W витков, пронизываемых одним и тем же потоком, индуктированная в нем ЭДС
равна: 
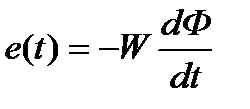
Часто различные группы витков (W1 , W2 ,...) одной и той же катушки пронизываются различными потоками
Ф1 , Ф2 , ...; в этом случае полная ЭДС катушки равна сумме ЭДС отдельных групп витков:
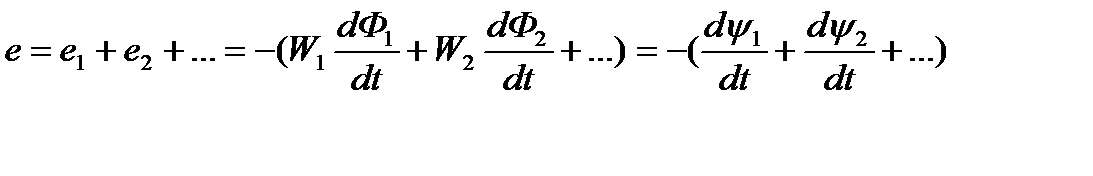

здесь 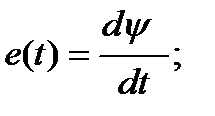
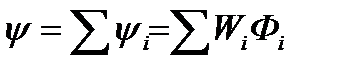 .
.
Сумму магнитных потоков, сцепленных с каждым из витков, называют магнитным потокосцеплением. Произведения W Ф являются потокосцеплениями соответствующих групп витков.
Уравнение, определяющее величину ЭДС как скорость изменения потокосцепления замкнутого контура представляет собой математическую формулировку закона электромагнитной индукции в наиболее общем виде. Знак "-" в нем определяется выбором условно положительных направлений индуктированной ЭДС и потока, пронизывающего контур.
|
При возрастании магнитного потока ( 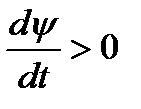 ) индуктированная ЭДС направлена противоположно выбранному положительному направлению. При убывании потока (
) индуктированная ЭДС направлена противоположно выбранному положительному направлению. При убывании потока ( 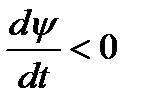 ) направление ЭДС совпадает с положительным направлением. Это соотношение получило название правило Ленца.
) направление ЭДС совпадает с положительным направлением. Это соотношение получило название правило Ленца.
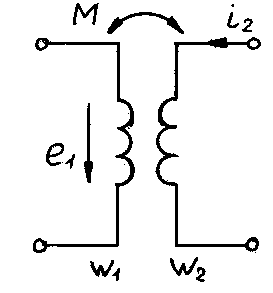
Общее выражение для индуктированной ЭДС справедливо и для цепей со взаимной индуктивностью. Пусть Ф2 - полный магнитный поток 2-й катушки, а ФM2 - его часть, пронизывающая 1-ю катушку. Тогда потокосцепление 1-й катушки будет равно
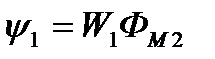
но оно относится и к току i :
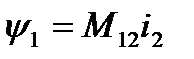
получаем формулу для взаимной индуктивности:
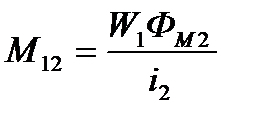
ЭДС, наведенную магнитным полем 2-й катушки в 1-й катушке, теперь удобно определить по формуле:
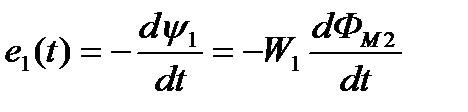
Пусть витки катушки пронизывает синусоидально изменяющийся магнитный поток:
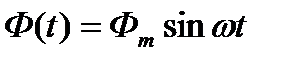
тогда, если пренебречь рассеянием поля, ЭДС, наведенная в витках катушки, определится выражением:
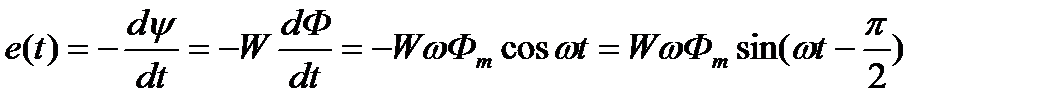
где 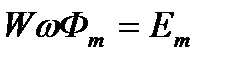 - амплитудное значение ЭДС. Ее действующее значение
- амплитудное значение ЭДС. Ее действующее значение
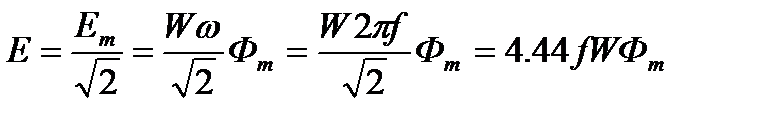
Это выражение часто используется на практике при расчетах различных машин переменного тока. Заметим, что ЭДС отстает по фазе от магнитного потока на угол 90 .
В цепях, содержащих катушки с ферромагнитными сердечниками, возникают из-за их нелинейности несиносоидальные токи и напряжения. Часто для упрощения анализа их заменяют эквивалентными синусоидальными величинами. Амплитуда эквивалентной синусоидальной величины определяется
произведением действующего значения несиносоидальной величины на 2, а фазовый сдвиг между эквивалентными синусоидами напряжения и тока определяются из соотношения:
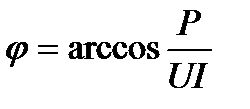
где параметры P, U и I относятся к несинусоидальным величинам. Переход к эквивалентным синусоидам позволяет вести анализ цепей символическим методом, а также строить векторные диаграммы на комплексной плоскости.
Дата добавления: 2016-02-16; просмотров: 1192;
