Катушка с ферромагнитным сердечником в цепи переменного тока.

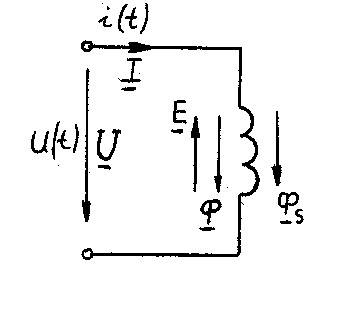
Рассмотрим цепь переменного тока, состоящую из катушки с ферромагнитным сердечником, к зажимам которой приложено синусоидальное напряжение

Пусть известны число витков катушки W, средняя длина магнитной линии l_ср, сечение сердечника S и сопротивление обмотки R.

Используя аналог 2-го закона Кирхгофа для магнитных цепей, можем записать:

H l_ср = I W = F,

где F - действующее значение НС обмотки, I - действующее значение тока в обмотке, Н - действующее значение напряженности магнитного поля в материале сердечника. Это же выражение можно записать и в комплексной (векторной) форме:

H l_ср = F

Отсюда нетрудно определить напряженность:

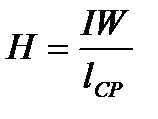
При гармоническом напряжении амплитуда магнитного потока, замыкающегося по сердечнику, определяется известным выражением:

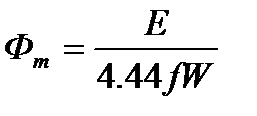
где Е - действующее значение ЭДС, наводимой в витках обмотки этим магнитным потоком.

Поток Ф, замыкающийся по сердечнику, называют основным, кроме него имеется еще магнитный поток рассеяния Ф_s, замыкающийся через воздух (поток рассеяния может быть сцеплен лишь с частью витков обмотки). Поскольку магнитное сопротивление воздуха значительно больше сопротивления сердечника, вектор Ф_s можно считать совпадающим по фазе с вектором тока I и пропорциональным ему. В таком случае общий поток можно представить как сумму двух составляющих:

Ф_общ = Ф + Ф_s.

Каждый из этих двух потоков пронизывает витки обмотки и наводит свою ЭДС. Поток Ф наводит ЭДС, действующее значение которой определяется выражением:

Е = 4,44 f W Ф_m

Поток рассеяния Ф_s наводит свою ЭДС Е_s, называемую ЭДС самоиндукции. Обычно эту ЭДС учитывают, вводя индуктивное сопротивление витков или сопротивление рассеяния X_s:

E_s = - j I X_s

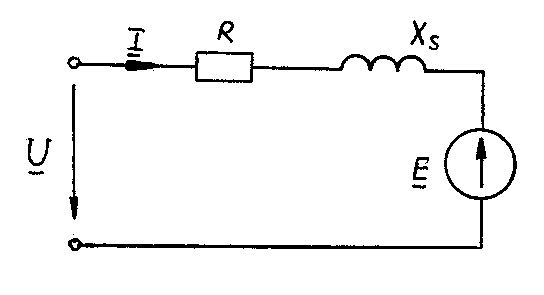
Если теперь учесть и активное сопротивление витков обмотки, то на основе полученных результатов можно построить схему замещения катушки с ферромагнитным сердечником:

В соответствии со 2-м законом Кирхгофа можем записать:

U + E = I R + j I X_s,

отсюда

U = - E + I R + j I X_s = - E + I Z;

это уравнение называют уравнением электрического состояния катушки с сердечником. Здесь Z = R + j X_s - комплексное сопротивление катушки, произведение

IZ = I R + j I X_s

является комплексом падения напряжения на витках катушки. По уравнению электрического состояния видно, что приложенное напряжение уравновешивается ЭДС, индуктированной основным магнитным потоком, и падением напряжения на витках катушки.

Если построить векторы магнитных величин в одной системе координат, получим диаграмму магнитного состояния. Напряженность Н и основной магнитный поток нам уже известны. Амплитуда индукции может быть

вычислена таким образом:

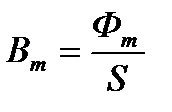
На практике падение напряжения IZ обычно невелико по сравнению с приложенным напряжением U, тогда полагают 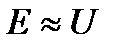и амплитуду магнитного потока определяют из приближенного соотношения:

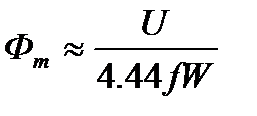
Порядок построения векторной диаграммы магнитного состояния таков:

1. Строим вектор основного магнитного потока Ф, считая его начальную фазу нулевой (т.е. располагаем его горизонтально).

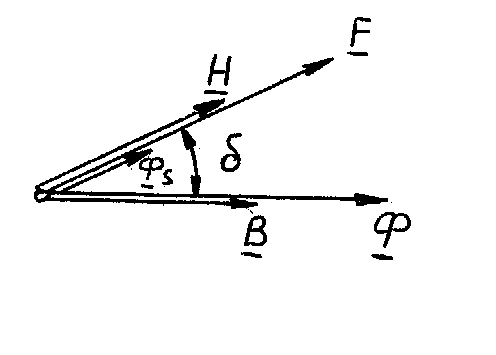
2. Строим совпадающий с ним вектор магнитной индукции В .

3. Строим опережающий их на угол магнитных потерь 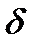вектор напряженности Н.

4. Строим совпадающие с вектором Н по направлению векторы НС обмотки F и магнитного потока рассеяния Ф_s.

На векторной диаграмме электрического состояния изображаются все векторы электрических величин, входящие в уравнение электрического состояния. Порядок построения векторной диаграммы таков:

1. За исходный принято считать вектор основного магнитного потока, его по-прежнему располагаем вдоль действительной оси.

2. Под углом 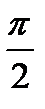к нему строится отстающий от него вектор ЭДС

3. Под углом 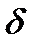к вектору основного потока Ф строится опережающий его вектор тока I (поскольку ток и напряженность магнитного поля совпадают по фазе).

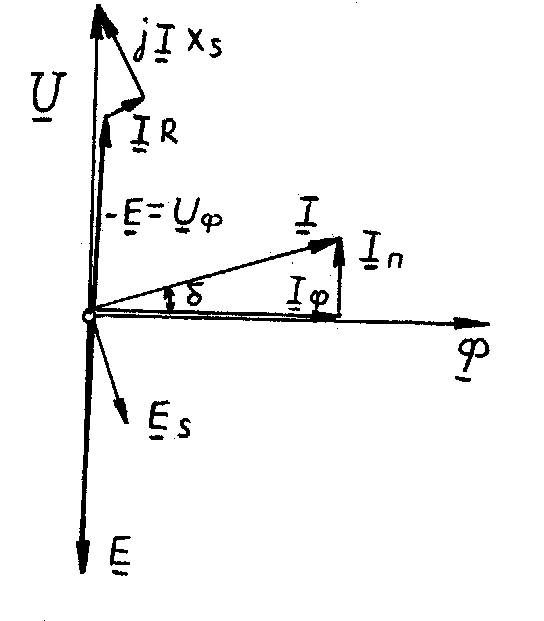
4. Дальнейшие построения ведутся в полном соответствии с уравнением электрического состояния: строится вектор -Е, противоположный вектору Е. К нему последовательно пристраиваются векторы I R, со впадающий по направлению с вектором I, и вектор j I X_s, опережающий вектор I на угол .

Соединяя начало координат с концом вектора j I X_s, получим вектор напряжения на зажимах катушки U.