Анализ вариации зависимой переменной
Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y.
Пусть на основе выборочных наблюдений построено уравнение регрессии 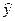 , тогда значение зависимой переменной y в каждом наблюдении можно разложить на две составляющие:
, тогда значение зависимой переменной y в каждом наблюдении можно разложить на две составляющие: 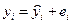 , где остаток ei есть та часть зависимой переменной y, которую невозможно объяснить с помощью уравнения регрессии.
, где остаток ei есть та часть зависимой переменной y, которую невозможно объяснить с помощью уравнения регрессии.
Разброс наблюдаемых значений зависимой переменной характеризуется выборочной дисперсией var(y).
Разложим дисперсию var(y):
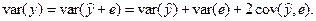
Поскольку 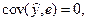 то
то
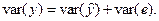
Таким образом, разложили дисперсию var(y) на две части:
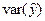 – часть, объясненную регрессионным уравнением;
– часть, объясненную регрессионным уравнением;
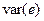 – необъясненную часть.
– необъясненную часть.
Коэффициентом детерминации R2 называется отношение
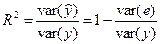 ,
, 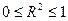 ,
,
характеризующее долю вариации (разброса) зависимой переменной, объясненнуюс помощью уравнения регрессии.
Отношение 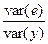 представляет собой долю необъясненной дисперсии.
представляет собой долю необъясненной дисперсии.
Если R2 = 1, то это означает точную подгонку:
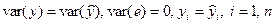 ,
,
т.е. все точки наблюдения лежат на регрессионной прямой.
Если R2 = 0, то регрессия ничего не дает:
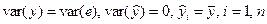 ,
,
т.е. переменная x не улучшает качества предсказания y по сравнению с горизонтальной прямой 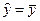 .
.
Чем ближе к единице R2, тем лучше качество подгонки, и 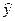 более точно аппроксимирует y.
более точно аппроксимирует y.
Замечание. Вычисление R2 корректно, если константа a включена в уравнение регрессии; при этом справедливо разложение 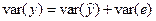 .
.
Пример 2.1. Покажем, что  , где
, где 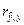 коэффициент корреляции между
коэффициент корреляции между 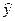 и y.
и y.
Действительно, учитывая соотношение:
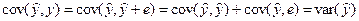 , получим
, получим
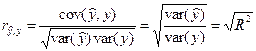

Пример 2.2.Покажем, что 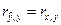 в случае парной регрессии
в случае парной регрессии 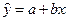 .
.
Действительно, из соотношений:
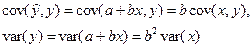
имеем: 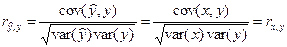 .
.
Вывод. В случае парной регрессии коэффициент детерминации есть квадрат коэффициента корреляции переменных x и y, т.е. R2 = r2x,y.
Пример 2.3.Зависимость переменной в регрессии 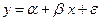 разбивается на две компоненты:
разбивается на две компоненты: 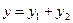 .
.
Рассмотрим две регрессии для компонент:
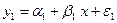 ,
,
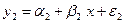
Докажем следующие соотношения для МНК-оценок параметров трех регрессий: a=a1+a2, b=b1+b2. Действительно,
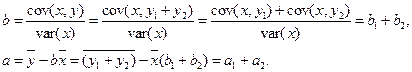
Пример 2.4.Покажем, что если все значения переменных изменить на одно и то же число или в одно и то же число раз, то величина коэффициента b в парной регрессии не изменится.
Пусть 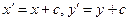 , тогда
, тогда
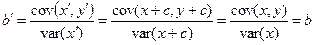 .
.
Пусть 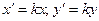 , тогда
, тогда
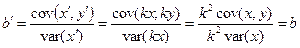
Дата добавления: 2016-02-16; просмотров: 3421;
