Метод наименьших квадратов. Модель парной регрессии

Модель парной регрессии

В модели парной линейной регрессии зависимость между переменными в генеральной совокупности представляется в виде:

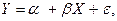(2.1)

где X – неслучайная величина, а Y и e – случайные величины.

Величина Y называется объясняемой (зависимой) переменной, а X – объясняющей(независимой) переменной. Постоянные a, b – параметры уравнения.

Наличие случайного члена e (ошибки регрессии) связано с воздействием на зависимую переменную других неучтенных в уравнении факторов.

На основе выборочного наблюдения оценивается выборочное уравнение регрессии (линия регрессии):

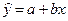, (2.2)

где (а; b) – оценки параметров (a; b).

Метод наименьших квадратов

Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений 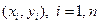линейным уравнением (2.2).

На рис. 8 приведены диаграмма рассеяния наблюдений и график линии регрессии.

Рис. 8

Величина описывается как расчетное значение переменной y_i, соответствующееx_i. Наблюдаемые значения y_i не лежат в точности на линии регрессии, то есть не совпадают с .

Определим остаток e_i в i-ом наблюдении как разность между фактическим и расчетным значениями зависимой переменной, т.е.

.

Неизвестные значения (a; b) определяются методом наименьших квадратов (МНК).

Сущность МНК заключается в минимизации суммы квадратов остатков:

.

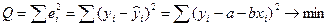Здесь (х_i, y_i) – известные значения (числа), (а; b) – неизвестные.

Запишем необходимые условия экстремума:

.

После преобразования получим следующую систему нормальных уравнений:

.

Решение системы:

(2.3)

Линия регрессии (расчетное значение зависимой переменной):

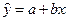,или .

Линия регрессии проходит через точку и выполняются равенства:

.

Коэффициентb есть угловой коэффициент регрессии и показывает, на сколько единиц в среднем изменяется переменная y при увеличении независимой переменной xна единицу.

Постояннаяa дает прогнозируемое значение зависимой переменной при x = 0. Это может иметь смысл в зависимости от того, как далеко находится x = 0 от выборочных значений x.

Можно показать, что

,

где r – коэффициент корреляции между x, y, а s_x, s_y – их стандартные отклонения.

Если коэффициент r уже рассчитан, то можно получить коэффициенты (a, b) парной регрессии.

После построения уравнения регрессии наблюдаемые значения y находим по:

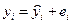. (2.4)

Остатки e_i, как и ошибки e_i являются случайными величинами, однако они, в отличие от ошибок e_i, наблюдаемы.

Докажем, что .

Действительно, используя равенства

,

получим

.

Определим выборочные дисперсии величин :

– дисперсия наблюдаемых значений y;

– дисперсия расчетных значений ;

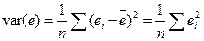– дисперсия остатков e.