Практическое применение СУ-схем

СУ-схемы предполагают существование отображения f: P₁ —> P₂ множества правил грамматики исходного языка в множество пра­вил грамматики объектного языка.

Выделяют два метода построения объектной программы путем преобразования исходной программы:

1 СУ-компиляция – строит объектную программу по ходу синтаксического анализа. В этом случае строить полное дерево разбора исходной программы, а тем более сохранять его после синтаксического анализа не требуется.

2 СУ-перевод – строит объектную программу после синтаксического анализа по его результату, представленным в виде дерева разбора.

Рассмотрим метод построения объектной про­граммы на основе СУ-перевода. В основу метода положено преобразование дерева разбора строки со во входной грамматике G_BX в дерево разбора выходной строки у в грамматике G_BbIХ. Метод позволяет получить перевод (w, у) любой входной строки w пу­тем последовательного решения следующих трех задач:

- построить дерево разбора w в грамматике G_BX;

- преобразовать полученное дерево в дерево разбора соответствующей строки у в грамматике G_BbIX, используя правила СУ-схемы;

- получить выходную строку у, взяв крону дерева разбора строки у.

Алгоритм преобразования дерева разбора входной строки

Обозначим: А — произвольный нетерминал СУ-схемы, А —> — правило входной грамматики, где = n₁…n_k . Пусть нетерминалу А соответствует узел А дерева разбора (нетерминальный узел). Тогда узлы n₁,n₂ , . . ., n_k - прямые потомки узла А. Преобразование дерева разбора начинается с его корня и состоит в следующем:

1) выбрать очередной нетерминальный узел А дерева разбора
входной строки; если все узлы обработаны, завершить работу;

2) устранить листья из множества узлов n₁…n_k (вершины,
помеченные терминалами или );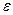

3) найти в СУ-схеме правило вида (А —> 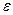, ) и переставить
оставшихся прямых потомков узла А в соответствии с их размещением в строке (поддеревья перемещать вместе с их корнями);

4) добавить в качестве прямых потомков узла А листья так,
чтобы метки всех его прямых потомков образовали цепочку ;

5) повторять п. 1—4 для всех прямых нетерминальных потом­
ков узла А по порядку, слева направо.

ПримерДана СУ-схема Т₂ = ({0, 1}, {S, A}, {a, b), R, S),где R содержит правила:

1) S->0AS,SAa 2) A->0SA,ASa 3) S->1,b 4) A->1,b.

На рис. 5.1.2а показано дерево разбора входной строки 00111. При­менение алгоритма преобразования к корню S этого дерева устраняет левый лист, помеченный 0 (шаг 2).

Рисунок 5.2 - Преобразование дерева разбора: а - дерево входной строки;

б - дерево после однократного применения алгоритма;

в - дерево выходной строки

Далее, так как корню соответ­ствует правило S -> 0AS и для этого правила = SAa, нужно поме­нять местами оставшихся прямых потомков корня (шаг 3). Затем сле­дует добавить а в качестве самого правого, третьего, прямого потом­ка (шаг 4). Результатом будет дерево, показанное на рис. 5.1.2б. Снова применяем алгоритм, теперь уже к первым двум потомкам корня. Обработка второго из них приводит еще к двукратному повторению алгоритма. Окончательный результат показан на рис. 5.1.2в, это дере­во разбора выходной строки bbbaa. Из анализа правил СУ-схемы Т₂ следует, что она является не простой постфиксной схемой.