Оптимизация кода для процессоров, допускающих распараллеливание вычислений
Многие современные процессоры допускают возможность параллельного выполнения нескольких операций. Как правило, речь идет об арифметических операциях.
Тогда компилятор может порождать объектный код таким образом, чтобы в нем содержалось максимально возможное количество соседних операций, все операнды которых не зависят друг от друга. Решение такой задачи в глобальном объеме для всей программы в целом не представляется возможным, но для конкретного оператора оно, как правило, заключается в порядке выполнения операций. В этом случае нахождение оптимального варианта сводится к выполнению перестановки операций (если она возможна, конечно). Причем оптимальный вариант зависит как от характера операции, так йот количества имеющихся в процессоре конвейеров для выполнения параллельных вычислений. Например, операцию A+B+C+D+E+F на процессоре с одним потоком обработки данных лучше выполнять в порядке ((((A+B)+C)+D)+Е)+F. Тогда потребуется меньше ячеек для храпения промежуточных результатов, а скорость выполнения от порядка операций в данном случае не зависит.
Та же операция на процессоре с двумя потоками обработки данных в целях увеличения скорости выполнения может быть обработана в порядке ((А+В)+С)+ +((D+E)+F). Тогда по крайней мере операции А+В и D+E, а также сложение с их результатами могут быть обработаны, в параллельном режиме. Конкретный порядок команд, а также распределение регистров для хранения промежуточных результатов будут зависеть от типа процессора.
На, процессоре с тремя потоками обработки данных ту же операцию можно уже разбить на части в виде (A+B)+(C+D)+(E+F). Теперь уже три операции А+В, C+D и E+F могут быть выполнены параллельно. Правда, их результаты уже должны быть обработаны последовательно, но тут уже следует принять во внимание соседние операции для нахождения наиболее оптимального варианта.
Формальные методы описания перевода
Синтаксически управляемый перевод
Схемы компиляции
Выделяют две основные схемы компиляции:
- последовательную;
- интегрированную.
Последовательная схема представляет собой - совокупность последовательно выполняемых программных компонентов, каждый из которых соответствует одному этапу компиляции (рис. 5.1.1). Последовательная схема предполагает не менее одного просмотра (прохода) программы на каждом этапе. Например, при генерации кода может выполняться два просмотра, а каждый метод машинно-независимой оптимизации требует по крайней мере одного просмотра. Рассмотренные методы построения промежуточной программы не требуют наличия разбора, и синтаксический анализатор может вообще не выполнять никакого преобразования программы. Последовательная схема, несомненно, проста и понятна, но она громоздка (по объему занимаемой памяти и времени компиляции программы) и применяется редко.
Интегрированная схема компиляции – схема, в которой компоненты выполняются под управлением синтаксического анализатора. Синтаксический анализатор, осуществляя разбор программы, вызывает лексический анализатор для сборки лексемы, когда в этом возникает необходимость. После завершения распознавания каждой синтаксической единицы программы вызывается семантический анализатор для ее обработки. Главная идея состоит в том, чтобы в ходе построения дерева разбора решать задачи последующих этапов компиляции для каждого вновь сформированного узла.
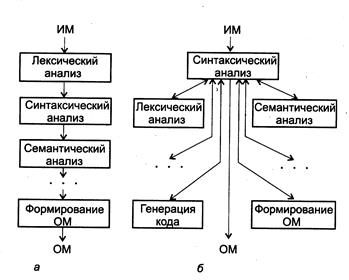
Рис. 5.1 - Схемы компиляции: а - последовательная,
б - интегрированная
Естественно, интеграция приводит к усложнению алгоритмов компиляции. Поэтому выбор подходящей структуры компилятора — непростая задача. Тем не менее, обычно строят компиляторы так, что на выходе синтаксического анализатора получается, как минимум, промежуточная программа в той или иной форме.
СУ-схемы
Интегрированные схемы компиляции базируются на теории перевода языков, ключевыми понятиями которой являются схема синтаксически управляемого перевода (СУ-схема), синтаксически управляемый перевод (СУ-перевод), преобразователь с магазинной памятью (МП - преобразователь). Рассмотрим эти понятия.
Определение. СУ-схемой Т называется пятерка следующих объектов
T={VT, VN, 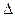 ,R,S), где
,R,S), где
VT — конечный входной алфавит, терминалы;
VN — конечное множество нетерминалов;
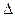 — конечный выходной алфавит;
— конечный выходной алфавит;
R — конечное множество правил вида A-> 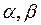 , где
, где 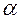
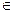 V*,
V*,
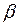
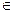 (VN
(VN 
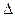 )*;
)*;
S — аксиома (начальный символ) схемы.
Определение. СУ-схема называется простой, если в каждом правиле А-> 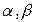 одноименные нетерминалы встречаются в
одноименные нетерминалы встречаются в 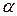 и
и 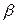 в одном и том же порядке. СУ-схема называется постфиксной, если
в одном и том же порядке. СУ-схема называется постфиксной, если 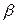
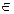 VN *
VN * 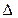 * в каждом правиле {А->
* в каждом правиле {А-> 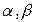 )
) 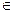 R.
R.
Определение. СУ-переводом 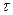 , определяемым (генерируемым) СУ-схемой T={VT, VN,
, определяемым (генерируемым) СУ-схемой T={VT, VN, 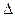 ,R,S), называется множество пар
,R,S), называется множество пар
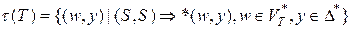
Грамматика GBX = {VT, VN, P,S), где Р = {А ->  | (А ->
| (А -> 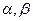 )
) 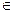 R}, называется входной грамматикой СУ-схемы. Грамматика GВЫХ ={
R}, называется входной грамматикой СУ-схемы. Грамматика GВЫХ ={ 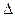 ,VN, P’,S), где P’ = {А ->
,VN, P’,S), где P’ = {А ->  | (А ->
| (А -> 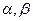 )
) 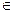 R}, называется выходной грамматикой СУ-схемы.
R}, называется выходной грамматикой СУ-схемы.
ПримерРассмотрим СУ-схему Т1 перевода арифметических выражений в обратную польскую запись. В основе этой схемы лежит соответствие правил записи арифметических выражений в обычной (инфиксной) форме и в ПОЛИЗ. Для упрощенных выражений такое соответствие приводится ниже.
Правила инфиксной формы Правила ПОЛИЗ
S->E S->E
E->E+T E->ET+
E->T E->T
T->T*F T->TF*
T->F T->F
F->(E) F->E
F-> имя F->имя
СУ-схема Т1 представляется пятеркой Т1 = {VT, VN, 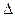 ,R,S), где S — аксиома, VT= {+, *, имя, (,)};
,R,S), где S — аксиома, VT= {+, *, имя, (,)}; 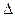 = {+, *, имя}; VN= {S, Е,T, F} и множество R содержит следующие правила:
= {+, *, имя}; VN= {S, Е,T, F} и множество R содержит следующие правила:
1)S ->E,E 2)E->E+T,ET+ 3)E->T,T 4)T->T*F,TF* 5)T->F,F 6)F->(E),E 7)F ->имя, имя
Входной грамматикой СУ-схемы Т1 является GВХ = (Vt, Vn, Р, S), где множество правил Р представлено правилами инфиксной формы. GВЫХ= ( 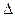 , Vn, P’ , S) — выходная грамматика СУ-схемы T1, а ее правила Р’ — это правила ОПЗ. Как показывает анализ правил СУ-схемы, Т1 — простая постфиксная СУ-схема. Нетрудно убедиться также, что в ней существует, например, вывод (S, S) =>* (a+b*c, abc*+), порождающий элемент перевода (а+b*с, abc*+)
, Vn, P’ , S) — выходная грамматика СУ-схемы T1, а ее правила Р’ — это правила ОПЗ. Как показывает анализ правил СУ-схемы, Т1 — простая постфиксная СУ-схема. Нетрудно убедиться также, что в ней существует, например, вывод (S, S) =>* (a+b*c, abc*+), порождающий элемент перевода (а+b*с, abc*+)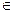
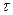 (T1).
(T1).
МП-преобразователи
МП - преобразователи позволяют формально описать соответствующие действия, связанные не только с распознаванием синтаксических конструкций, но и с построением дерева разбора (вывода) и его преобразованием, а также действия, которые имеют как синтаксический, так и семантический характер.
Определение. МП - преобразователем называют восьмерку вида
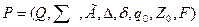
Q - конечное множество состояний преобразователя;
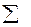 - конечный входной алфавит;
- конечный входной алфавит;
Г - конечный магазинный алфавит;
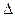 - конечный выходной алфавит;
- конечный выходной алфавит;
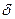 - отображение множества (Q * (
- отображение множества (Q * ( 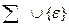 * Г) в множество всех подмножеств множества (Q * Г**
* Г) в множество всех подмножеств множества (Q * Г** 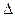 *), т.е.
*), т.е. 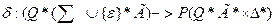
qо - начальное состояние преобразователя, q0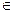 Q;
Q;
Zo - начальное содержимое магазина, Zo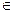 Г;
Г;
F - множество заключительных состояний преобразователя, F 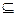 Q.
Q.
Определение. Конфигурация МП - преобразователя — это четверка (q,w,  , у)
, у)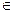 (Q х
(Q х 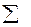 * х Г* х
* х Г* х 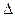 *). Начальная конфигурация — (q0 ,w, Zo,
*). Начальная конфигурация — (q0 ,w, Zo, 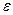 ), заключительная конфигурация — (q,
), заключительная конфигурация — (q, 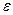 ,
,  , у), где q
, у), где q 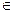 F. Если одним из значений функции
F. Если одним из значений функции 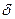 (q, a, Z) является (q’,
(q, a, Z) является (q’, 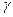 , r), то шаг работы преобразователя можно представить в виде отношения на конфигурациях
, r), то шаг работы преобразователя можно представить в виде отношения на конфигурациях
(q, aw, Za, у) |- (q’,wо, 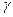 а, уr) для любых w
а, уr) для любых w 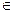
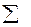 *,
*, 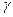
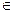 Г*, у
Г*, у 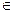
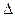 *.
*.
Строка у будет выходом МП - преобразователя для строки w, если существует путь от начальной до заключительной конфигурации
(qо, w, Zo, 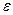 ) |-* (q,
) |-* (q, 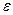 ,
,  , у) для некоторых q
, у) для некоторых q 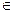 F и
F и 
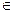 Г*.
Г*.
Определение. Переводом (преобразованием) 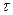 , определяемым МП - преобразователем Р, называется множество
, определяемым МП - преобразователем Р, называется множество
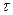 (Р) = {(w,у) | (q0,w, Zo,
(Р) = {(w,у) | (q0,w, Zo, 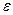 )|-* (q,
)|-* (q, 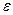 ,
,  ,у) для q
,у) для q 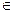 F,
F, 
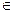 Г*.
Г*.
Определение. МП - преобразователь будет детерминированным, если, как и МП - автомат, он имеет не более одной возможной очередной конфигурации. Расширенный МП - преобразователь отличается от рассмотренного только магазинной функцией
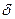 : (Q х (
: (Q х ( 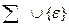 ) х Г*) -> P(Q х Г* х
) х Г*) -> P(Q х Г* х 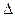 *).
*).
Теперь обратимся к двум результатам теоретических исследований, имеющим чрезвычайно важное практическое значение. Они состоят в следующем.
1. Если T={VT, VN, 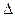 ,R,S) - простая СУ-схема с входной грамматикой LL(k), то СУ-перевод
,R,S) - простая СУ-схема с входной грамматикой LL(k), то СУ-перевод 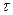 (Т) можно осуществить детерминированным МП - преобразователем.
(Т) можно осуществить детерминированным МП - преобразователем.
2. Если T={VT, VN, 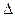 ,R,S) - простая постфиксная СУ-схема с входной грамматикой LR(k), то перевод
,R,S) - простая постфиксная СУ-схема с входной грамматикой LR(k), то перевод 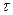 (T) можно выполнить детерминированным МП - преобразователем.
(T) можно выполнить детерминированным МП - преобразователем.
Существуют алгоритмы, позволяющие построить детерминированный МП - преобразователь по заданной СУ-схеме перевода. В их основе лежат алгоритмы построения таблиц разбора.
Простые СУ-переводы образуют важный класс переводов, поскольку для каждого из них можно построить детерминированный МП - преобразователь, отображающий входную строку (цепочку) в выходную строку (цепочку). Такие переводы иногда называют цепочечными.
Дата добавления: 2016-03-27; просмотров: 654;
