В) применение эффективных процедур уточнения решений.

Численные методы решения систем нелинейных алгебраических уравнений (СНАУ)

Цель:изучить систематизированную основу теоретических знаний численных методов решения систем нелинейных алгебраических уравнений.

Учебные вопросы:

4.1. Постановка задачи

4.2. Метод простых итераций

4.3. Метод Зейделя

4.4. Метод Ньютона

Литература к лекции 4: [1], с.69…74, 66…68; [2], с.43…48;

[3], с.46…55.

Постановка задачи

При численном решении систем нелинейных алгебраических уравнений предполагается выполнение трех условий:

А) существование искомого вектора решений;

Б) возможность нахождения начального приближения искомого вектора;

в) применение эффективных процедур уточнения решений.

Дана система нелинейных уравнений, для которой нужнонайти вещественное решение с заданной точностью ,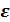

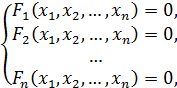(1)

или 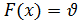, (1а)

где: ,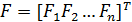

,

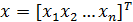имеем начальное приближение: .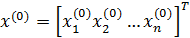

В случае системы двух нелинейных уравнений начальное приближение находят графически, как показано на Рис.1.

Рис.1. Графическое решение СНАУ

В общем случае не существует метода определения начального приближения! Но если начальное приближение 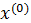известно, то уточнение начального приближения можно осуществить тремя методами:

методом простых итераций, методом Зейделя и методом Ньютона.

Результат уточнения 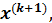удовлетворяющий условию

,

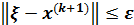является решением СНАУ (1) .