Метод простых итераций

Для использования метода простых итераций система СНАУ (1)записывается в эквивалентной форме

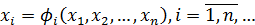, (2)

где 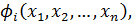– эквивалентныефункции.

Эквивалентные функции строятся по аналогии с лекцией 3 в виде

.

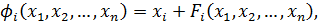
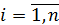Тогда, если известно начальное приближение 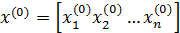, можно построить алгоритм простых итераций:

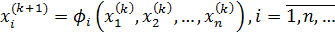. (3)

Доказано, что алгоритм (3) сходится к решению системы СНАУ (1), если какая-либо норма матрицы Якоби, построенной по эквивалентным функциям, меньше единицы на каждой итерации: т.е.

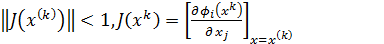(3а)

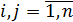, k= 0,1,2,…

Метод простых итераций останавливается при выполнении условия

,

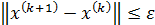где 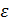– заданная ошибка решения СНАУ (1).

Тогда искомый вектор .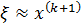

Таким образом, метод простых итераций применяется для дифференцируемых функций 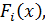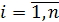, в системе нелинейных алгебраических уравнений (1).

Метод Зейделя

Метод Зейделя уточнения решения СНАУ заключается в использовании на (k+1)-ой итерации результатов, полученных в (k+1)-ой итерации, для последующих вычислений в этой же (k+1)-ой итерации.

Метод Зейделя ускоряет сходимость метода простых итераций. Он строится на основе метода простых итераций.

Алгоритм метода Зейделя имеет вид:

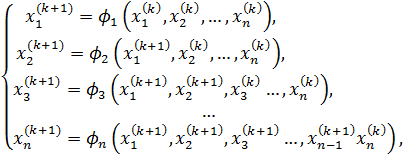(4)

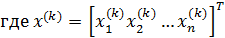– известное k-ое приближение;k= 0,1,2,… .

Условие сходимости метода Зейделя аналогично условию сходимости метода простых итераций (3а).

Метод Зейделя останавливается при выполнении условия

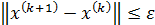, (4а)

где 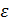– заданная ошибка решений СНАУ (1).

Тогда искомый вектор .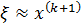

Метод Ньютона

Имеем систему нелинейных алгебраических уравнений (1). Определено начальное приближение 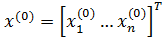. Метод Ньютона решения СНАУ сводится к последовательному решению СЛАУ, полученных путем линеаризации системы нелинейных алгебраических уравнений (1).

Для известного k -го приближения вектора неизвестных

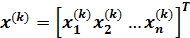будем искать 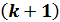-е приближение в виде

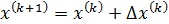, k=0,1,2,… , (5)

где вектор приращений 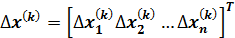подлежит определению.

Для нахождения этих приращений разложим функцию 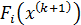в ряд Тейлора в окрестности точки 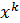до производных первого порядка включительно (оставим только линейную часть относительно 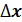) и приравняем это разложение нулю, т.е.

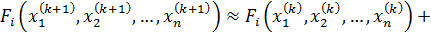
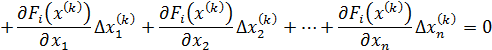
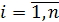
Осуществляя те же процедуры для остальных уравнений системы (1), получим следующую СЛАУ относительно вектора неизвестных :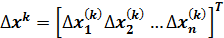

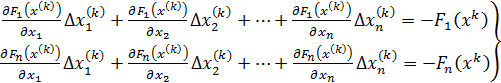(6)

Для существования единственного решения СЛАУ (6) необходимо и достаточно, чтобы матрица этой СЛАУ

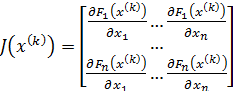– матрица Якоби для СНАУ (1),

была невырожденной 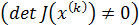, т.е. существовала обратная матрица 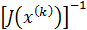. Определитель матрицы Якоби называютякобинами СНАУ (1) .

Запишем СЛАУ (6) в векторно-матричной форме:

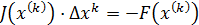, (7)

откуда

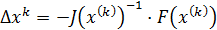. (8)

Подставляя (8) в (5), получим алгоритм Ньютона решения СНАУ (1):

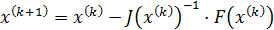, (9)

имеем начальное приближение

,

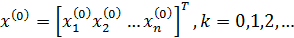(сравнить (9) с методом Ньютона для одного нелинейного уравнения

).

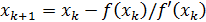Итерационный процесс (9) заканчивается при выполнении условия 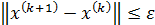, где 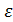– заданная точность, а искомый вектор

.

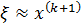Таким образом, для применения алгоритма метода Ньютона (9) необходимо выполнение двух условий:

1) существование частных производных первого порядка от функций 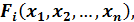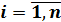, по всем переменным ;

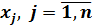2) матрица Якоби для СНАУ (1) на каждой итерации k=0,1,2,… должна быть не вырождена.

При выполнении указанных двух условий алгоритм Ньютона всегда сходится к точному решению СНАУ (1), т.е.

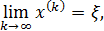где 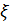– точное решение СНАУ (1).