Мережі, вільні та залежні. Необхідність зрівняльних обчислень.
Як відомо, кінцева мета створення геодезичної мережі полягає в одержанні координат пунктів. Для її досягнення в мережі тріангуляції необхідно мати одну вихідну сторону, що визначає масштаб мережі, один вихідний дирекційний кут для її орієнтування й один пункт з вихідними координатами. Ці необхідні вихідні дані можуть бути задані і координатами двох вихідних пунктів. Якщо в мережі маються вихідні дані понад необхідні, то вони є надлишковими.
Геодезична мережа, що складається тільки з необхідних вихідних даних, називається вільною, а яка має дані понад необхідну-залежною. Геодезичні мережі, що підлягають зрівноваженню, як правило, містять надлишкові вихідні дані.
Для визначення координат пунктів геодезичної мережі крім вихідних необхідно мати і ряд виміряних величин, до яких відносяться напрямки (кути), довжини сторін і азимути. Так, наприклад, у мережі тріангуляції для визначення координат пунктів С, D, Е, F, Н при заданих А та В необхідно і достатньо виміряти в кожному трикутнику по два кути (відзначені дугами), що будуть необхідними виміряними величинами.
Основною ж метою зрівнювання геодезичних мереж, як згадувалося вище, є відшукування таких поправок у результати виміряних величин, які б усували нев'язки в геометричних умовах мережі. Очевидно, що наслідком цього усунення буде рівність між собою значень будь-якого елемента геодезичної мережі, обчисленого різними способами (одержання координат пункту З по координатах вихідних пунктів А и В).
Також як і в тріангуляції в полігонометричних ходах і мережах крім необхідних виконують виміри і надлишкових величин, наявність яких дозволяє поставити задачу врівноваження.
При врівноваженні полігонометричних ходів відповідно до методу найменших квадратів застосовують:
строгі способи врівноваження, при цьому поправки знаходять під умовою
[pbn2b] + [psn2s] = min;
Нестрогі способи (роздільні), коли поправки в виміряні кути і прирости координат одержують окремо, зневажаючи їх взаємною залежністю.
Строге врівноваження полігонометричних ходів виконують корелатним або параметричним способами, а також їх комбінаціями. Вибір способу врівноваження обумовлений максимально можливою економією трудових витрат при обчисленнях.
МОГВ)
Питання. Принцип найменших квадратів. Основні шляхи рішення задачі врівноваження.
У1806 р. французький математик Лежандр запропонував спосіб рішення невизначених систем лінійних рівнянь, невідомими в яких є поправки в результати вимірів, що одержав назву метод найменших квадратів. У цьому способі рівняння підпорядковуються додатковій умові - сума квадратів поправок v, щовводяться в рівноточні виміри, повинна дорівнювати мінімумові, тобто менше суми квадратів будь-якої іншої системи поправок, що задовольняє даним рівнянням:
v21 + v22 +…+v2n=min... (42)
При нерівноточних вимірах додаткова умова має вигляд:
p1v21+p2v22+ …+pnv2n = [pv2] = mіn... (43)
Умова (43) є математичним виразом принципу найменших квадратів.
Таким чином, із усієї безлічі можливих рішень системи рівнянь вибирається одне, що задовольняє умові (43). Математична обробка результатів вимірів деякої сукупності величин з дотриманням вимоги (43) називається зрівнюванням за методом найменших квадратів.
З математичної сторони це являє собою наступну задачу.
Потрібно знайти мінімум функції (43), якщо її перемінні v зв'язані з незалежними рівняннями (42).
Для рішення такої задачі в математичному аналізі застосовуються два основних способи:
- спосіб Лагранжа з невизначеними множниками;
- спосіб абсолютного екстремума, заснований на представленні всіх виміряних величин у вигляді функцій деяких параметрів.
У теорії математичної обробки результатів геодезичних вимірів перший спосіб називається корелатним (спосіб умов або умовних вимірів), другий - параметричним (спосіб необхідних невідомих або посередніх (непрямих) вимірів).
МОГВ)
Питання: Врівноваження системи ходів з однією вузловою точкою з оцінкою точності.
Зрівнювання системи нівелірних ходів з одною вузловою точкою виконують в такій послідовності:
1. Складають схему нівелірних ходів, нумерують ходи і стрілками показують напрями нівелювання.
2. На схему виписують суми перевищень по кожному ходу , довжини окремих нівелірних ходів в кілометрах і відмітки вихідних точок.
3. Визначають величини нев’язок в перевищеннях по найбільш коротких ходах, включаючи всі перевищення. Якщо нев’язки не перевищують допуски існуючих інструкцій, то зрівнюють ходи.
4. Обчислюють висоти вузлової точки по кожному ходу.
5. Ваги ліній обчислюють за формулою 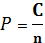
C – постійний коефіцієнт, його беруть кратним 10 і з таким розрахунком, щоб вага лінії, як правило, знаходилася в межах від 1 до 10; n – число штативів в даній лінії. Якщо число штативів на 1 км ходу приблизно однакове для всіх ліній системи, то ваги ліній обчислюють за формулою
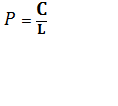 , L – довжина лінії в км.
, L – довжина лінії в км.
6. Обчислюють найімовірніше значення відмітки вузлової точки.
7. Обчислюють поправки в перевищення по кожному ходу.
8. Виконують оцінку точності. Обчислюють середні квадратичні помилки:
а) одиниці ваги m :
, де n – число ходів в системі
б) середню квадратичну помилку найімовірнішого значення відмітки H Д 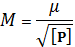
в) середню квадратичну помилку нівелювання на 1 км ходу: км 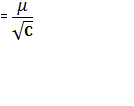
9. Обчислюють відмітки всіх точок нівелірних ходів. Для цього кожний хід зрівнюють, як окремий хід між двома твердими реперами. Величини поправок по кожному ходу розподіляють з протилежним знаком пропорціонально довжинам секцій в ходу.
МОГВ)
Питання. Врівноваження системи нівелірних ходів з кількома вузловими точками методом послідовних наближень
На початку зрівнювання нівелірних ходів складають схему нівелірної мережі. На схемі показують всі вихідні пункти з висотами, вузлові точки, напрями передачі висот по кожному ходу, перевищення в ходах з номером і знаком, довжини холів, а також обчислюють нев’язки в ходах, охоплюючи всі вимірювання. Після нього складають схему зрівнювання нівелірних ходів. В графу 1 записують номери вузлових точок, відмітки яких зрівнюються.
В графу 2 записують назви точок від яких будуть обчислюватися відмітки вузлових точок.
В графу 3 записують відмітки вихідних точок, а в графу 4 виписують суми перевищень по кожному хочу в напрямі на вузлову точку. В графу 5 записують довжини ходів в км. За формулою 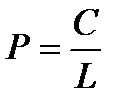 обчислюють ваги кожного ходу, їх суми на вузлових точках і записуюсь в графу 6. Для зручності наступних обчислень на кожній вузловій точні обчислюють з точністю до 0.01 приведені ваги (графа 7) за формулою:
обчислюють ваги кожного ходу, їх суми на вузлових точках і записуюсь в графу 6. Для зручності наступних обчислень на кожній вузловій точні обчислюють з точністю до 0.01 приведені ваги (графа 7) за формулою: 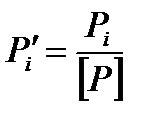 ,
,
де 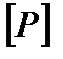 – сума ваг ліній, які сходяться в даній точці;
– сума ваг ліній, які сходяться в даній точці;
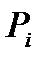 – вага лінії з номером “
– вага лінії з номером “ 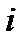 ”.
”.
Правильність обчислення приведених ваг контролюється їх сумою, тобто 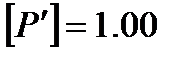 . В графу 8 записують відмітки вузлових точок, обчислених в першому наближенні
. В графу 8 записують відмітки вузлових точок, обчислених в першому наближенні
Обчислені відмітки вузлових точок в першому наближенні приймаємо за вихідні для обчислення відміток вузлових точок кожного ходу в другому наближенні (графа 9), додаючи перевищення до уже обчислених відміток в першому наближенні
Із обчислених трьох значень відміток першої вузлової точки в другому наближенні обчислюють середнє вагове і результат записують в рядок 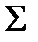 .
.
Такі обчислення виконують в другому наближенні для інших вузлових точок. Аналогічно обчислюють відмітки вузлових точок в наступних наближеннях, беручи відмітки вузлових точок попереднього наближення для обчислення відміток вузлових точок наступного наближення.
Число наближень вважається достатнім, якщо розходження між результатами останнього і передостаннього наближення збігаються. Значення відміток, які одержали в останньому наближенні, вважаються зрівняними (найімовірнішими) відмітками вузлових точок. Після цього обчислюють поправки “ 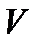 ”, які слід ввести в перевищення кожної лінії (графа 13). Поправки “
”, які слід ввести в перевищення кожної лінії (графа 13). Поправки “ 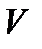 ” обчислюють як різниці між зрівняними значеннями відміток вузлових точок і тими числами в графі останнього наближення, із яких обчислено значення зрівняних висот, як середнє вагове. Контролюють правильність обчислення кінцевих відміток точок і поправок “
” обчислюють як різниці між зрівняними значеннями відміток вузлових точок і тими числами в графі останнього наближення, із яких обчислено значення зрівняних висот, як середнє вагове. Контролюють правильність обчислення кінцевих відміток точок і поправок “ 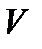 ” в перевищення:
” в перевищення: 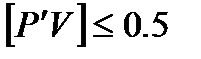 мм.
мм.
Оцінка точності за результатами зрівнювання полягає в обчисленні середньої квадратичної помилки одиниці ваги “ 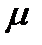 ” і середньої квадратичної помилки нівелюванню на 1 км ходу “
” і середньої квадратичної помилки нівелюванню на 1 км ходу “ 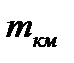 ”.
”.
Для оцінки точності кожного ходу обчислюють величини 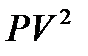 і їх суму для всієї системи холів. Середня квадратична помилка одиниці ваги обчислюється за формулою:
і їх суму для всієї системи холів. Середня квадратична помилка одиниці ваги обчислюється за формулою:
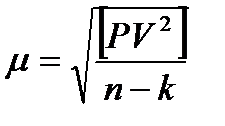
де 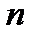 – число ходів і
– число ходів і 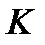 – число вузлових точок в мережі.
– число вузлових точок в мережі.
Середню квадратичну помилку нівелювання на один кілометр ходу обчислюють за форму- лою: 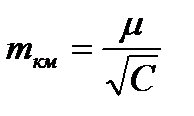 . Якщо для обчислення ваг величину “
. Якщо для обчислення ваг величину “ 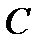 ”
”
МОГВ)
Питання 5. Врівноваження системи нівелірних ходів з кількома вузловими точками методом «червоних чисел» з оцінкою точності.
Мережу нівелірних ходів називають незалежною, якщо вона не прив’язана до реперів державної нівелірної мережі, або прив’язана тільки до одного репера. Такі мережі зручно зрівнювати способом полігонів В.В.Попова.
Для цього складають схематичний рисунок мережі полігонів з зазначенням номерів вузлових точок і полігонів, довжин ходів (в кілометрах), сум перевищень і числа штативів (станцій) кожної ланки.
На рис. 3 - А – вихідна нівелірна марка; В, С, D – вузлові точки, які не мають відміток; 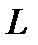 – довжина ланок в кілометрах;
– довжина ланок в кілометрах; 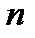 – число штативів; стрілками показано напрями з додатними перевищеннями.
– число штативів; стрілками показано напрями з додатними перевищеннями.
Безпосередньо, згідно з рисунком, підраховують нев’язки в сумах перевищень по кожному полігону, визначаючи знаки нев’язок для напрямів, що збігаються з ходом годинникової стрілки. Визначають якість виміряних перевищень шляхом порівняння одержаних нев’язок з допустимими, обчисленими згідно з вимогами нівелювання ІV кл. за формулою: 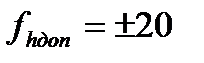 мм
мм 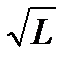 .
.
В наведеній формулі 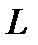 – довжина ходу, виражена в кілометрах.
– довжина ходу, виражена в кілометрах.
Обчислені і допустимі нев’язки записують на рисунку в середині відповідних полігонів. (Рис.3).
Рис.3
Складають схему полігонів для зрівнювання перевищень (Рис.4) і указують на ній номера вузлових точок і полігонів.
На цій схемі в середині кожного полігона, під його номером, заготовляють табличку нев’язок (в міліметрах), а біля кожної ланки – табличку поправок, при цьому по зовнішніх ланках – по одній табличці з зовнішньої сторони, а по внутрішніх лаках – по дві таблички з обох сторін кожної ланки.
Після цього обчислюють з точністю до 0.01 червоні числа для кожної ланки кожного полігона за правилом: червоне число ланки дорівнює числу штативів ланки, поціленому на число штативів всього полігона (або довжині ланки в км поділеному на периметр всього полігона).
Для ланок АВ, ВD і DА першого полігона (Рис.4) відповідно будемо мати такі червоні числа: 0.45, 0.33 і 0.22. Сума червоних чисел в кожному полігоні повинна дорівнювати 1. Червоні числа виписують над відповідними табличками червоним кольором. Безпосередньо на схемі розподіляють нев’язки, починаючи з найбільшої за абсолютною величиною в такій послідовності: множать нев’язку даного полігона послідовно на кожне червоне число його ланки. (В нашому прикладі для ІІІ полігона, з якого почали зрівнювання, одержали поправки +25, +8, +14). Одержані добутки записують в зовнішні таблички поправок під відповідними червоними числами з знаком нев’язки і сума всіх добутків повинна дорівнювати величині нев’язки, тобто нев’язці III полігона. На схемі розподілену нев’язку підкреслюють.
Переходять до сусіднього полігона І. В табличні нев’язок записують під нев’язкою полігона нову, одержану, як алгебраїчну суму нев’язки з поправкою, винесеною за рахунок спільної ланки з сусіднього полігона (+38)+(+8)=(+46). Нову нев’язку множать послідовно на червоні числа кожної ланки даного полігона, і одержані добутки записують в відповідні таблички поправок, контролюючи їх суму, яка повинна дорівнювати величині нев’язки.
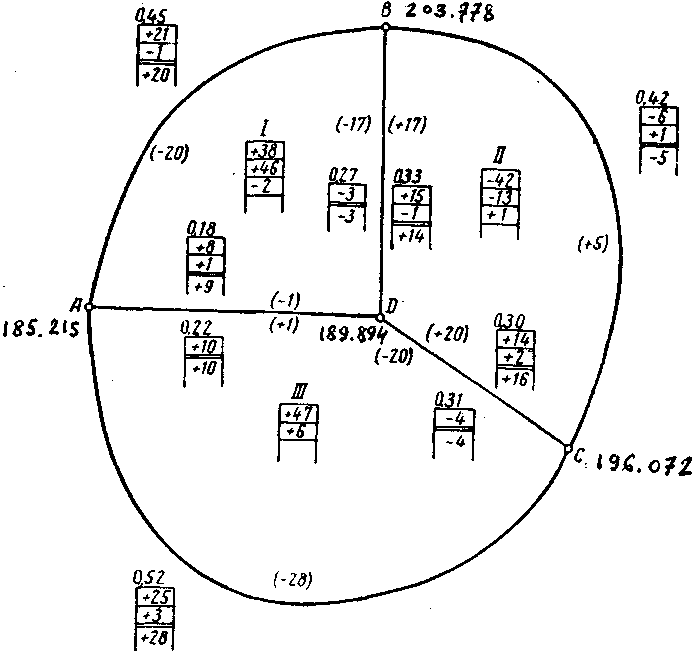
Рис.4
Після цього переходять по наступного, II полігона, підраховують його нову нев’язку, в якій враховані внесені за рахунок спільних ланок поправки з сусідніх полігонів (-42)+(+15)+(+14)=(-13), з цією нев’язкою поступають так само, як описано в попередніх полігонах.
Закінчивши, таким чином, перший круг, переходять знову до початкового полігона. Підраховують його нову нев’язку, яка складається з алгебраїчної суми поправок, внесених з спільних ланок сусідніх полігонів (+10)+(-4)=(+6). Записують її в табличку нев’язок, множать послідовно на червоні числа ланок. Одержані добутки записують в відповідні таблички поправок і контролюють суми добутків. Потім, переходячи послідовно від полігона до полігона, поступають аналогічно до тих пір, поки нев’язки всіх полігонів будуть дорівнювати нулю, тобто будуть винесені за зовнішні межі полігонів.
Після закінчення розподілу нев’язок підраховують алгебраїчну суму поправок в кожній табличці і записують її під подвійною лінією. Обчислюють поправки в сумах перевищень по кожній ланці і записують їх на схемі, в дужках, біля відповідної ланки з внутрішньої сторони полігона.
Поправка в суму перевищень внутрішньої ланки дорівнює алгебраїчній сумі чисел зовнішньої таблички поправок, взятої з протилежним знаком, плюс алгебраїчна сума чисел внутрішньої таблички поправок.
Наприклад, в II полігоні:
для ходу СD поправка буде: -(-4)+(+16)=(+20)
для ходу DВ поправка буде: -(-3)+(+14)=(+17)
для ходу ВС поправка буде: -(-5)+0=(+5)
Обчислені поправки записують в таблицю зрівнювання полігонів, (таблиця 5).Алгебраїчна сума поправок по кожному полігону, повинна дорівнювати величині нев’язки з протилежним знаком.
Після обчислення поправок в перевищення виконують оцінку точності нівелювання, тобто обчислюють середню квадратичну помилку одиниці ваги і середню квадратичну помилку нівелювання на 1 км ходу 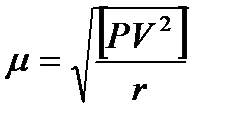 ,
,
де 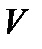 – поправка в суму перевищень ланки
– поправка в суму перевищень ланки
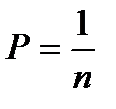 – число, обернене кількості штативів ланки;
– число, обернене кількості штативів ланки; 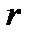 – число полігонів.
– число полігонів.
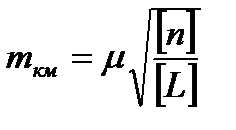 ,
,
де 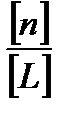 – середнє число штативів на 1 км ходу.
– середнє число штативів на 1 км ходу.
Таблиця 5
| № полігонів | Ланки | 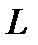 , км , км
| 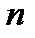
| 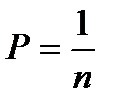
| Нев’язки полігонів, мм | Червоні числа | 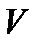
| 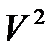
| 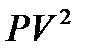
|
| І | AB BD DA | 6.0 4.6 3.4 | 0.02 0.03 0.04 | 0.45 0.33 0.22 | -20 -17 -1 | 8.0 8.3 0.0 | |||
| 14.0 | +38 | 1.00 | -38 | ||||||
| ІІ | CD DB BC | 5.3 4.6 7.9 | 0.03 0.03 0.02 | 0.31 0.27 0.42 | +20 +17 +5 | ¾ | 10.3 ¾ 0.5 | ||
| 17.8 | -42 | 1.00 | +42 | ||||||
| ІІІ | CA AD DC | 10.2 3.4 5.3 | 0.01 0.04 0.03 | 0.52 0.18 0.30 | -28 +1 +20 | ¾ ¾ | 11.7 ¾ ¾ | ||
| 18.9 | +47 | ||||||||
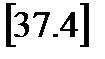
| 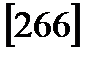
| 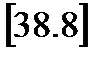
|
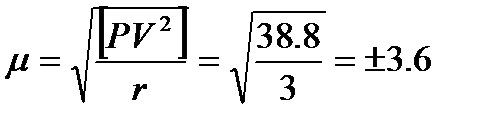 мм;
мм; 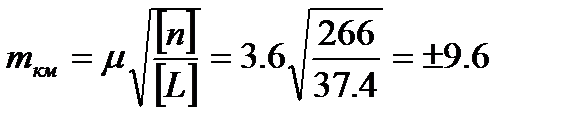 мм
мм
За вихідною відміткою марки А і відповідних сум перевищень з урахуванням поправок обчислюють відмітки вузлових точок В, С, D, контролюючи їх за всіма наявними напрямами
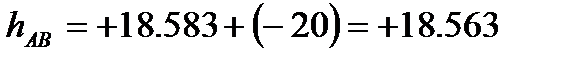
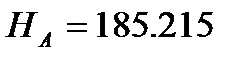
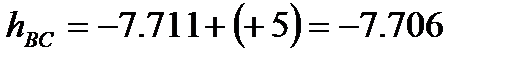
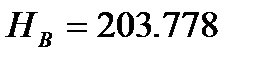
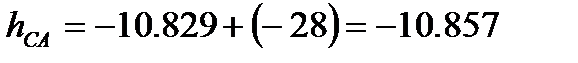
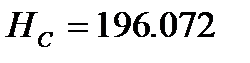
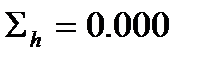
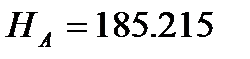
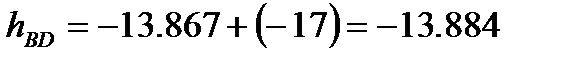
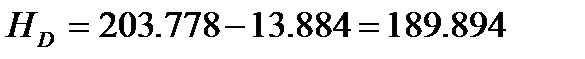
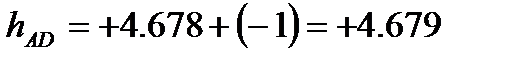
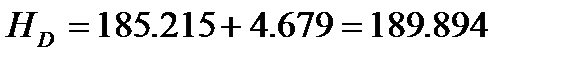
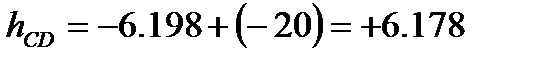
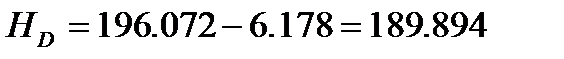
Обчислення відміток можна виконувати безпосередньо на схемі, або в відомості обчислення відміток.
МОГВ)
Питання: Врівноваження систем ходів розрядної полігонометрії з однією та з кількома вузловими точками.
При зрівнюванні полігонометричних мереж з надлишковим числом вихідних даних доцільно застосовувати розроблений проф. В. В. Поповим спосіб вузлів. Він одержав велике поширення у варіанті з рішенням нормальних рівнянь способом послідовних наближень, унаслідок чого одержав відповідну назву.
Розглянемо зрівнювання способом вузлів на прикладі полігонометричної мережі 1 розряду (див. мал. 5).
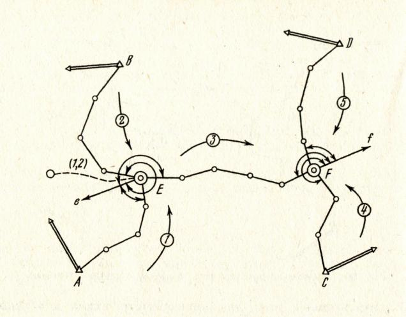
Мал. 5
Для цього позначимо зрівняні значення дирекційних кутів вузлових напрямків аЕ і аF, а дирекційні кути вихідних напрямків aА, aВ, aС и aD. Тоді для aЕ и aF можна написати наступні вирази:
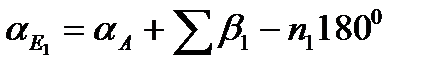
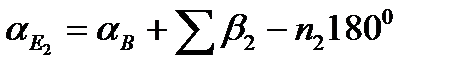
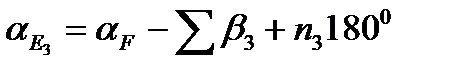
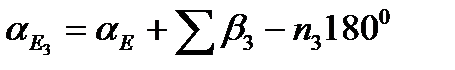 (44)
(44)
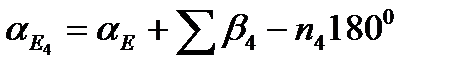
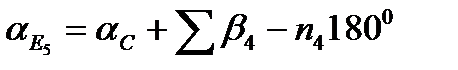
де aEi і aFi (i=1,2,3,4,5) -значення дирекційних кутів вузлових напрямків aEe і aFf , обчислених по і-му ходу;
Sbi,-сума лівих кутів у i-ому ході; ni — число кутів у i-их ходах.
Введемо позначення
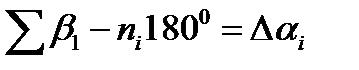 (45)
(45)
Тоді, використовуючи вираз (44) і (45), для ходів зрівнюваної мережі можна написати наступні параметричні рівняння виправлень:
aE -(aA + Da1) = vDa1;
aE -(aB + Da2) = vDa2;
-aE + DaF –(Da3) = vDa3; (46)
a -(a + Da4) = vDa4;
a -(a + Da5) = vDa5;
У рівняннях (46) = vDai — поправки у величини Dai, що на підставі прийнятих позначень дорівнюють сумі поправок в виміряні кути відповідного ходу, тобто vDai=S vDbi, а величини в дужках є вільними членами цих рівнянь.
Для визначення ваги величин vDai використовуємо формулу 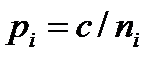
Вирішуючи параметричні рівняння поправок (46) під умовою [pv2 ] = min, одержимо наступні нормальні рівняння:
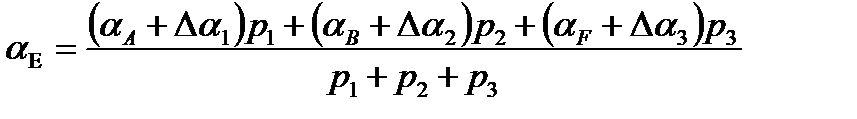
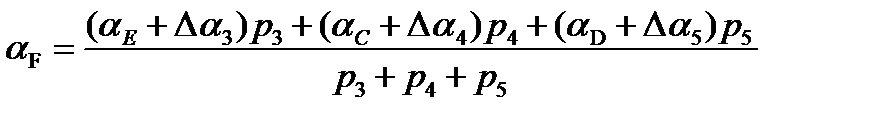 (47)
(47)
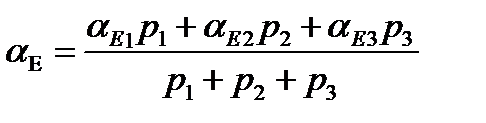
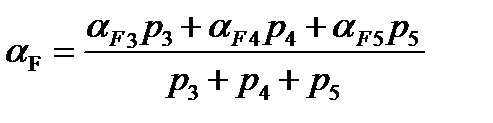 (48)
(48)
За формулами (48) одержують зрівняні значення дирекційних кутів вузлових напрямків. При цьому попередні значення дирекційних кутів цих напрямків аЕ1, аЕ2, аЕ3 і а3, а4, а5 , що входять у праві частини зазначених формул, обчислюють по формулах (44).
Однак у правих частинах формул (48) поряд з дирекційними кутами вихідних напрямків аА, ав , ас і аD маються і зрівняні значення дирекційних кутів напрямків аЕ й аF, що невідомі на початку обчислень. Тому обчислення за формулами (48) виконують способом послідовних наближень, що полягає в наступному.
Спочатку за формулами (44) одержують наближені значення дирекційного кута одного з вузлових напрямків, що має найбільше число зв'язків з вихідними напрямками, а потім за формулами (48) його зрівняне значення з першого наближення. Аналогічно знаходять зрівняні значення дирекційних кутів інших вузлових напрямків у першому наближенні з урахуванням їх зв'язків з вихідними і суміжними вузловими напрямками. Причому для останніх приймають значення, отримані з першого наближення.
Таким чином, для кожного вузлового дирекційного кута визначають його зрівняне значення з другого, третього і т.д. наближень. При цьому в кожнім наближенні при обчисленні по за формулами (44) використовуються значення дирекційних кутів вузлових напрямків, з'єднаних ходами зі врівноваженим вузловим напрямком, отримані в попереднім або поточному наближеннях.
Так, для нашого випадку значення дирекційного кута аЕ в першому наближенні обчислюють як середнє вагове з аЕ й аF отриманих з ходів 1 і 2, а значення дирекційного кута аE2 як середнє вагове з а3, а4, а5, визначених відповідно з ходів 3, 4 і 5. Відмітимо, що при обчисленні а3 використовується значення аЕ з першого наближення.
Друге наближення дирекційного кута аЕ одержують як середнє вагове зі значень аЕ1, аЕ2, і аЕ3 з трьох ходів 1, 2 і 3. Причому аЕ3 одержують, використовуючи аF з першого наближення.
Обчислення продовжують доти, поки значення врівноваженого дирекційного кута для усіх вузлових напрямків у двох сусідніх наближеннях не буде однаковим. Збіжність наближень обумовлена тим, що задача вирішується під умовою [pv2 ] = min.
Одержавши зрівняні значення дирекційних кутів вузлових напрямків, обчислюють кутові нев'язання Wbi = - Snbi по всіх ходах. Потім, переконавшись в їх допуску, розподіляють нев‘язки порівно в усі кути, і після цього обчислюють дирекційні кути сторін ходів, а також прирости координат.
Врівноваження абсцис і ординат вузлових пунктів виконують аналогічно врівноваженню дирекційних кутів, якщо у формулах (47) і (48) замінити Da й a сумами приростів і координатами з тими ж індексами. При цьому ваги визначають за формулами (47) або (48).
Знаючи зрівняні значення координат вузлових пунктів, підраховують по кожному ходу нев'язки
Wхi =хі – хвр; Wуi =уі – хвр;
і звичайним спрощеним способом зрівнюють кожен хід окремо з обчисленням координат пунктів.
Оцінка точності врівноважених значень елементів полігонометричної мережі виконується за формулами:
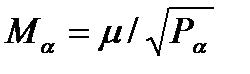
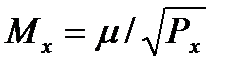
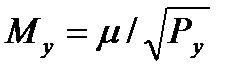 - середня квадратична помилка дирекційного кута та координат пунктів.
- середня квадратична помилка дирекційного кута та координат пунктів.
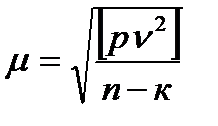 -середня квадратична помилка одиниці ваги.
-середня квадратична помилка одиниці ваги.

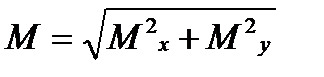 -середня квадратична помилка розташування вузлового пункту мережі.
-середня квадратична помилка розташування вузлового пункту мережі.
Причому ваги врівноважених значень дирекційних кутів вузлових напрямків і координат вузлових пунктів знаходять способом еквівалентної заміни.
МОГВ)
Питання: Параметричний метод врівноваження геодезичних мереж. Основні формули рішення задачі.
Дата добавления: 2016-03-27; просмотров: 3413;
