Об'єднання GPS з інерціальними навігаційними системами (ІНС).
ІНС складається з гіроскопа (виконує кутову стабілізацію аерокамери
підчас нахилу літака) та акселерометра (визначає зміну швидкості польоту
літака). Об'єднання GPS та ІНС суттєво доповнюють одне одного.
Відомо, що стабільність показів GPS є високою в доволі великому часовому
періоді, але в коротких проміжках часу можуть виникати певні труднощі, в
основному через втрату сигналів від супутників підчас навігаційного
маневру. ІНС навпаки – дають добрі покази в коротких часових проміжках,
але у великих часових періодах спотворюються впливом т.зв.
гіроскопічного ефекту та систематичними похибками акселерометрів, що
мають тенденцію до накопичення.
Об'єднання GPS та ІНС дає доповнюючий ефект: в короткочасових проміжках
ІНС "поправляє" дані GPS, а в довгих часових проміжках GPS компенсує
систематичні похибки ІНС.
Інтегровані навігаційні системи (GPS + ІНС), як згадувалось, є тепер
невід'ємною частиною цифрових аерознімальних комплексів. Вони дозволяють
фіксувати кути нахилу знімальної камери з точністю 10//-20//, що в
багатьох випадках задовільняє розв'язання фотограмметричних задач.
Стримуючим фактором у широкому використанні таких систем є їх висока
вартість та проблеми інсталяції на невеликих (але економічних) літальних
апаратах.
ФТГМ
1. Основні елементи центральної проекції аерознімка та математична залежність між ними.
a. Основні елементи центральної проекції
Коли вважати, що на аерофотознімку відсутні деформації фотоматеріалу, вплив дисторсії об’єктива фотокамери, атмосферної рефракції та інших джерел похибок, то одержане зображення можна прийняти за центральну проекцію об’єкта на площину. Основні елементи центральної проекції показані на рис. 3.5.
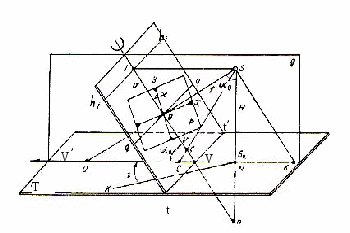
Рис. 3.5 – Основні елементи центральної проекції
Горизонтальна площина Т, в якій розміщені точки проектування, називається предметною або площиною основи.
Площина Р, на яку проектуються точки місцевості, називається картинною площиною або площиною знімка. У загальному випадку ця площина буває нахиленою по відношенню до предметної площини.
Площини Т і Р вважаються нескінченними і обмеження їх лініями є умовним. Точка S – це центр проекції.
Кут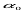 
між предметною і картинною площинами називаються кутом нахилу знімка.
Проектуючий промінь ^ So, перпендикулярний до площини знімка, називається головним променем. Він повинен збігатися з оптичною віссю об’єктива АФА. Точка o перетину головного променя з площиною знімка називається головною точкою.
Кут між напрямом головного променя ^ So і прямовисною лінією SN дорівнює куту нахилу знімка 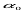. Якщо 
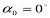, то площина знімка ^ Р горизонтальна.
Відстань So від центра проекції до площини знімка позначається через f і називається фокусною відстанню фотокамери.
Точка n перетину прямовисного проектуючого променя SN з площиною знімка називається точкою надіра. Вона є зображенням точки місцевості N, яка в момент фотографування знаходилась на прямовисній лінії з передньою вузловою точкою об’єктива АФА.
Точка с – точка нульових спотворень знаходиться на перетині бісектриси кута 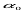з площиною знімка.
Вертикальна площина ^ Q, яка проходить через головний промінь So і прямовисний промінь SN, називається площиною головного вертикала.
Перетин площини Q з площиною Р, який позначено лінією vv', називається головною вертикаллю знімка.
Лінія V V' – перетин площин Q і Т – лінія напряму знімання.
Горизонтальний проектуючий промінь, який знаходиться в площині головного вертикала ^ Q перетинає площину Р в головній точці сходу І.
Важливо відмітити, що всі чотири точки І,o,c та n нахиленого знімка розміщені на його головній вертикалі.
Лінії hihi, qq, які розміщені в площині Р перпендикулярно до головної вертикалі, називаються горизонталями фотознімка.
Лінія tt' перетину предметної і картинної площин називається лінією основи картини.
Лінія hihi є лінією дійсного горизонту. На цій лінії розміщуються зображення нескінченно віддалених точок місцевості.
Лінія qq – горизонталь, яка проходить через головну точку знімка, називається головною горизонталлю.
Горизонталь, яка проходить через точку с, є лінією неспотвореного масштабу. При перетині вздовж цієї лінії площин нахиленого і горизонтального знімків масштаб зображення на обох знімках буде однаковим.
Із трикутників Son і SoI можна визначити віддалі між важливими елементами центральної проекції за формулами:
;
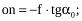
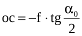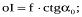
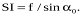
Знак "-" вказує, що позитивний напрям осі – вздовж головної вертикалі від точки о до I.
Точка С в предметній площині відповідає точці нульових спотворень с, точка N – відповідає точці надіра n фотознімка.
2. Спотворення точок на аерофотознімках через його кут нахилу
4. Зсув точок на аерознімку через його нахил
Уявимо, що нахилений і горизонтальний аерознімки одержані однією фотокамерою і мають загальний центр проекції S (рис. 4.9).
В цьому випадку знімки перетинаються по горизонталі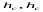 
, яка проходить через точку нульових спотворень с, а пряма Sс зображує бісектрису кута нахилу знімка 
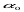, фокусні відстані знімків Р і Р0 однакові.
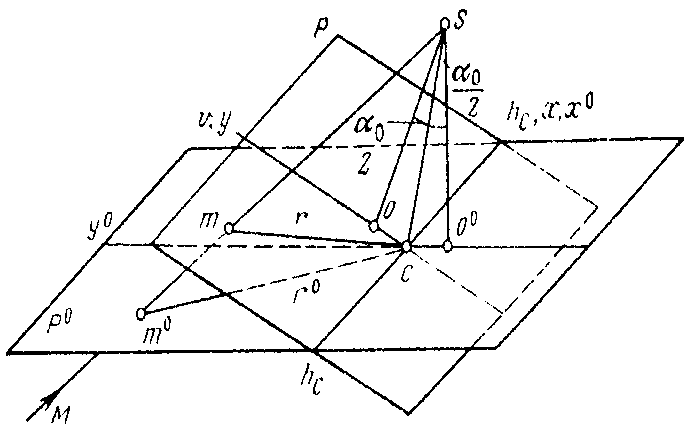
Рис. 4.9 – Схема зсуву точки аерознімка через його нахил
Позначимо через m i m0 зображення точки місцевості М на нахиленому і горизонтальному знімках. Проведемо радіуси r i r0 від точки с до точок m i m0 . Кути між радіусами r i r0 і лінією 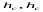однакові. Тому, якщо знімок Р повернути навколо горизонталі 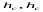і сумістити із знімком Р0, то радіуси r i r0збіжаться, а точка m нахиленого знімка буде зсунута відносно точки m0 горизонтального знімка в напрямі сm0. Отже, нахил знімка викликає радіальний зсув точок.
Точка m, яка знаходиться вище лінії 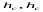, із збільшенням кута 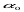наближається до точки нульових спотворень с і, навпаки, точка к, розташована нижче лінії 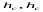, віддаляється від точки с (рис. 4.10.).
Точка l, яка знаходиться на лінії неспотвореного масштабу, займає однакове положення на нахиленому і горизонтальному знімках.
П
,
означимо через x і y координати точки m на нахиленому знімку Р, а через x0 і y0 – координати точки m0 на горизонтальному знімку.
Якщо початок координат знаходиться на знімку в точці нульових спотворень с, а на місцевості – у відповідній їй точці С, то можемо записати:
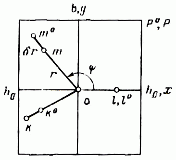
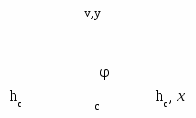
Рис. 4.10 – Вплив кута нахилу знімка на зсув зображення
,
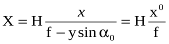
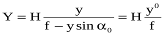
де X,Y – координати точки місцевості М;
Н – висота фотографування відносно місцевості, яка приймається за горизонтальну площину.
З цих формул виходить, що
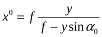
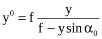
Знайдемо величину радіуса – вектора 
на горизонтальному знімку:
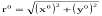
Підставивши в цей вираз значення x0 і y0, одержимо
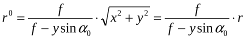
З рис. 4.10 виходить, що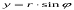 
. Підставимо це значення в одержану вище формулу, запишемо
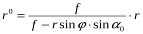
Тепер знайдемо величину зсуву точки знімка
,
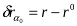викликане кутом нахилу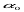 
. Можемо записати:
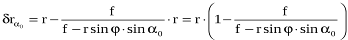або
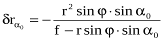
З 
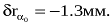цієї формули виходить, що максимальне значення 
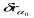буде при найбільшому значенні r і 
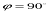, тобто для точки, яка розміщена на головній вертикалі і максимально віддалена від точки нульових спотворень. Так, для планового аерознімка 
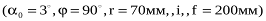одержимо
Коли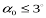 
формулу величини зсуву точки знімка можна представити у вигляді:
. 
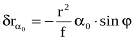
3. Спотворення точок на аерознімках через рельєф місцевості
Дата добавления: 2016-03-27; просмотров: 898;