Зсув точок на аерознімку через вплив рельєфу місцевості

Вертикальні прямі на місцевості (опори ліній електропередач, заводські труби, дерева) зображуються на аерофотознімках не у вигляді точок, а мають вигляд відрізків, які сходяться в точку надіра.

На рис. 4.11 показаний розріз вертикальною проектуючою площиною ^ SANB горизонтального знімка Р і місцевості з вираженим рельєфом. Точки А і Вмають перевищення – h_a і h_b відносно горизонтальної площини Т, прийнятої за початкову. Точки А₀ і В₀ – ортогональні проекції точок А,В на площину Т. На топографічному плані точки А і А₀ зобразились би однією точкою, те ж саме стосується і точок В,В₀.

Рис. 4.11 – Вертикальний розріз горизонтального знімка

рельєфної місцевості

На горизонтальному знімку Р, як видно з рис. 4.11, зображення точок А і В місцевості і їх ортогональні проекції на початкову площину не збігаються.

Так, промінь, що проектує точку ^ В, дає її зображення на знімку в точці b, а промінь, що проектує точку В₀, дає її зображення в точці b₀.

Відрізок bb₀ представляє собою зсув зображення точки, обумовлений впливом рельєфу місцевості. Цей же відрізок є зображенням вертикальної прямої ВВ₀на знімку. Точкою на аерофотознімку зображується тільки вертикальна пряма, що проходить через точку N. На горизонтальному знімку точка надіра n збігається з головною точкою о.

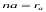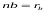Позначимо і , а також 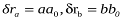та через відрізок , через – відрізок .

Зсуви точок через вплив рельєфу відносно початкової площини Т направлені на знімку від точки надіра при h>0 і до точки надіра – при h<0.

В загальному випадку зсув . Визначимо зсув в залежності від перевищення h=BB₀.

Продовжимо проектуючий промінь SB до перетину з площиною Т в точці В₁. Прямі nb і NB₁ паралельні, а промені SB₁,SB₀ та SN відтинають на них пропорційні відрізки. Тому

З подібності трикутників SNB₁ і BB₀B₁ знаходимо

,

де Н₀ – висота фотографування над початковою площиною.

Із одержаних рівностей виходить:

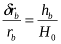
Враховуючи знак і знак перевищення h, одержимо формулу:

Аналізуючи цю формулу, бачимо, що зсув через рельєф зменшується із збільшенням висоти фотографування Н₀. Тому для зменшення зсувів точок через вплив рельєфу, аерознімки необхідно одержувати з найбільших висот. Зсув точок через рельєф прямо пропорційний відстані даної точки від точки надіра і досягає максимального значення на краях знімка.

Так, наприклад, при Н₀ = 2000 м, h = 100 м і r = 70 мм величина 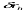дорівнює +3,5 мм.

Можна визначити радіус кола, в межах якого зсув 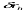не перевищує допустимої величини спотворень координат точок:

.

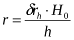Наприклад, якщо на знімку, одержаному аерофотоапаратом з f = = 200 мм у масштабі 1:25000, спотворення не повинні перевищувати 0,3мм, то при h = 25 мr = 60 мм.

Коли 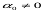, тобто знімок нахилений, то одночасно виникає зсув точок через кут нахилу 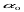і через рельєф місцевості.

У випадку, коли початок координат на знімку знаходиться в точці надіра, а на місцевості в точці ^ N, проекції зсуву точки нахиленого знімка на координатні осі x і y через рельєф будуть:

,

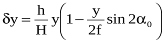
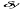Враховуючи значення і , а також те, що і 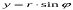, одержують величину сумісного впливу кута нахилу 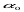і рельєфу за формулою

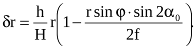
На плановому знімку

і, якщо знімок горизонтальний,

де Н – висота фотографування відносно місцевості, яка приймається за горизонтальну площину.

4. Маштаб горизонтального і нахиленого фотознімків аналіз формули горизонталям.

Масштаб зображення горизонтальної ділянки плоскої місцевості на горизонтальному знімку є сталою величиною, яка має вираз відношення 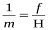, де f – фокусна відстань аерофотоапарата, Н висота польоту.

В загальному випадку масштаб аерознімка є величиною змінною. Він змінюється як із переходом від однієї точки відрізка до іншої, так і зміною напряму відрізку, що вимірюють.

Масштаб зображення аерознімка визначається відношенням нескінченно малих відрізків на знімку і на горизонтальній місцевості

,

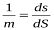де – два відповідних нескінченно малих відрізка на площині нахиленого знімка і на горизонтальній площині місцевості (рис. 4.12).

На знімку прийнята система координат сху з початком в точці нульових спотворень с , вісь х направлена по лінії неспотвореного масштабу, вісь у – вздовж головної вертикалі.

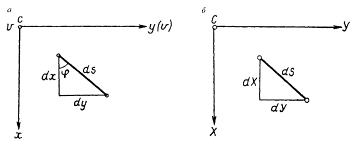
Рис. 4.12 – Нескінченно малі відрізки на знімку (а) і на місцевості (б)

На місцевості початком системи координат прийнята точка ^ С, зображення якої на знімку збігається з точкою нульових спотворень, а за напрями осей Х і У– проекції осей х і у знімка.

Напрям відрізка 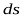на знімку визначається кутом 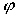відносно лінії неспотвореного масштабу, з якою суміщена вісь х системи координат. Проекції відрізка 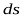на осі х і у мають значення:

(1)

Довжину відрізка на горизонтальній площині визначимо через його проекції на осі Х і Y:

,

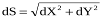і тому масштаб знімка буде мати вигляд:

(2)

Для визначення величин dX i dY використаємо відповідні формули для нахиленого знімка:

Здиференціюємо ці рівняння по змінним х і у:

Підставивши замість dx і dy їх значення з (1), одержимо:

(3)

Позначивши 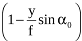через к і 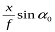– через с, одержимо:

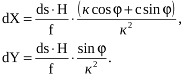
Підставивши значення dX i dY в (2), будемо мати:

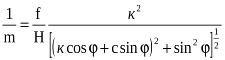(4)

Аналіз одержаної формули підтверджує, що масштаб зображення на нахиленому знімку є величиною змінною і в данній точці і по різних напрямах розрізняється.

Але для будь-якої горизонталі 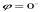і тому , , 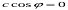а коефіцієнт к не залежить від абсциси точки. Звідси виходить, що масштаб вздовж горизонталі – величина стала.

Застосовуючи формулу (4), обчислимо масштаб зображення в характерних точках нахиленого знімка по напряму головної вертикалі і по напрямам, перпендикулярним до неї (горизонталям).

1. Масштаб зображення в точці нульових спотворень с по напряму головної вертикалі. В цьому випадку , , , , ,

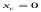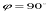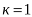П
к
о напряму лінії неспотвореного масштабу – , , 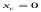, , , 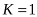маємо

Отже, масштаб зображення в точці нульових спотворень і по горизонталі, що проходить через точку с, дорівнює масштабу зображення на горизонтальному знімку. Тому цю горизонталь називають лінією неспотвореного масштабу.

2. Масштаб зображення в головній точці знімка о:

п о головній вертикалі , , ,

;

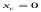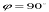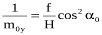по горизонталі , , )

.

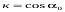3. Масштаб зображення в точці надіра, n.

По головній вертикалі, коли , , , .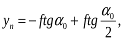

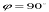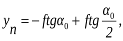
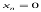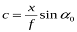П о горизонталі – , , має значення

4. Масштаб зображення в головній точці сходу I.

П 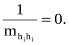о головній вертикалі , , , , 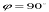c = 0) –

масштаб по горизонталі, що проходить через точку ^ I,

Масштаб у будь-якій точці знімка, віддаленій від точки нульових спотворень с на 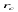, при напрямі, відхиленому від головної вертикалі на кут , дорівнює:

де 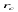– відстань від точки нульових спотворень с до точки знімка, 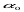– кут нахилу знімка, – кут між напрямом на знімку, виміряний в точці с від головної вертикалі проти ходу стрілки годинника.

5. Штучний стереоефект, умови його отримання, стерео модель місцевості. Спосіб вимірговання стерео моделі за допомогую уявної марки

Пространственное восприятие можно получить не только при непосредственном рассматривании объекта в натуре, но и при рассматривании стереопары снимков этого объекта.

Представим себе, что с точек S₁ и S₂ сделаны два снимка Р₁ и Р₂ рассматриваемого объекта (точки F и A, рис. 47) Поставим эти снимки перед глазами наблюдателя так, чтобы проектирующие лучи проходили через изображения соответственных точек на снимках (точки а¢₁,¢₂, и f¢₁, f¢₂,). При рассматривании каждого снимка (левого Р₁ – левым глазом, а правого Р₂ – правым) изображения точек объекта получаются в тех же точках сетчаток, что и при рассматривании самого объекта, и вследствие разностей физиологических параллаксов возникает впечатление объёмного изображения.

Пространственное восприятие объекта при бинокулярном рассматривании пары снимков, полученных с разных точек пространства, называется стереоскопическим эффектом, а воспринимаемая при этом мнимая картина – стереоскопической моделью.

Для получения стереоэффекта, кроме названных выше условий необходимо, чтобы:

1. Разность масштабов снимков стереопары не превышала 16 %.

2. Каждым глазом наблюдался только один из снимков.

3. Угол, под которым пересекаются соответственные лучи, не превышал 16°.

4. Положение снимков было согласовано с глазным базисом. В первом приближении это осуществляется расположением снимков на линии, параллельной глазному базису.

При рассматривании пары снимков можно получить прямой, обратный или нулевой стереоэффекты (рис. 48). Стереоскопический эффект получается прямым (естественное восприятие пространства), если снимки расположить перекрытием внутрь; обратным (обратное восприятие выпуклых и вогнутых форм), если их расположить перекрытием в разные стороны.

Если снимки повернуть на 90° в разные стороны, то возникает нулевой стереоэффект, при котором рассматриваемый объект воспринимается плоским.

Для обеспечения второго условия получения стереоэффекта используют: анаглифический, поляроидный, миганий, растровый, оптический и другие способы.

В способе анаглифови левое изображение и правое проецируют на один экран через светофильтры красный и зеленый (синий). Полученная картина рассматривается через анаглифические (красно-зеленые) очки. В результате каждый глаз видит только одно изображение, а при их слиянии возникает стереоэффект в серо-белых тонах.

В способе поляроидовиспользуют не цветные, а поляроидные светофильтры с углом поляризации между ними 90°. Через них рассматривают проецируемые на экран поляризованные с таким же углом изображения. В отличие от анаглифического способа, поляроидный может использоваться для наблюдения цветных снимков, поэтому используется в кинематографии.

В способе миганий снимки проектируются на экран поочерёдно с помощью, например, вращающихся перед объективами бленд. Такие же бленды установлены перед глазами наблюдателя. Частота вращения обеих пар бленд синхронизирована и составляет не менее 10 миганий в секунду. Таким образом, наблюдатель непрерывно видит левым глазом только левое изображение, а правым – только правое. Способ используется для получения объемной картины и на экране монитора.

При растровом способе два снимка проектируются на экран, составленный из линз цилиндрической формы. Оптические лучи, несущие изображения разных снимков, отражаясь противоположными гранями линз экрана, попадают в разные глаза наблюдателя.

Оптический способ основан на разделении зрения с помощью оптических систем. Этот способ имеет широкое применение в фотограмметрии. Простейшими оптическими приборами, позволяющими получить пространственное изображение сфотографированного объекта, являются стереоскопы.

Имеются линзовые стереоскопы, которые предназначены для рассматривания малоформатных снимков (6x6 см). Для работы с аэрофотоснимками, как в полевых, так и в камеральных условиях, используют зеркальные стереоскопы с бинокулярной насадкой или линзово-зеркальные стереоскопы.

Линзово-зеркальный стереоскоп ЛЗ (Рис. 49) имеет две пары зеркал 1, 2 и 1¢, 2¢, установленных под углом 45° к плоскости горизонтально расположенных снимков; и две линзы 3 и 3¢. Пунктиром на рисунке показан ход центральных лучей, O₁ и O₂ – узловые точки глаз (центры хрусталиков). Расстояния от центров линз 3 и 3¢ до снимков по ходу центральных лучей называются главными расстояниями стереоскопа, а отрезок между центрами больших зеркал 2 и 2¢ - базисом стереоскопа d. Если считать, что расстояние наилучшего зрения равно 250 мм, то увеличение стереоскопа V=250/d. Для получения стереокартины снимки следует устанавливать так, чтобы расстояние между соответственными точками примерно равнялось длине базиса стереоскопа, а отрезки между парой соответственных точек располагались на одной прямой параллельной его направлению. В зависимости от расположения снимков стереоэффект будет прямой, обратный или нулевой.

Стереоскопическое измерение снимков можно выполнять способами действительной и мнимой марки. Первый из них - уже практически история. Он применялся при монокулярном измерении снимков, а также при измерении модели, построенной по паре снимков с помощью поляроидов и анаглифов в некоторых проекционных приборах (мультиплексе, двойном проекторе и т.д.).

Способ мнимой марки предложен в 1899 г. Пульфрихом и используется для измерения координат точек пары снимков и модели. Суть его состоит в следующем. В плоскости изображений (снимков) располагают две действительные марки m₁ и m₂ (на рис. 50 показаны крестиками). При их рассматривании под стереоскопом в одну объемную картину сливаются не только изображения снимков, но и марок, то есть наблюдатель видит одну пространственную мнимую марку M. Но это произойдет только в случае, когда каждая из марок m₁ и m₂ будет расположена вблизи соответственных точек (например, а₁.и а_2). Причем, небольшое взаимное перемещение действительных марок (или снимков относительно марок) вдоль оси x вызовет перемещение мнимой марки по глубине. В результате она будет казаться либо «висящей в воздухе», либо «утопленной в землю». В последнем случае мнимая марка раздваивается, что дает возможность оценить поперечный параллакс. Когда действительные марки точно совмещены с соответственными точками (например, а₁.и а₂), создается впечатление касания мнимой марки поверхности стереомодели в точке А. Для того, чтобы этого добиться, стереоприбор должен обеспечивать совместное движение снимков (действительных марок) вдоль осей x и y, а также независимое движение одного из снимков (одной из марок), вдоль этих же осей. При наличии соответствующих шкал на таком приборе можно измерять параллаксы.

Наиболее простым прибором для измерения только продольных параллаксов p точек, является параллаксометр. Его принципиальная схема представлена на Рис. 51. На общем металлическом стержне 1 расположены две стеклянные пластинки с марками m₁ и m₂ и фиксатор 2. Марка m₂ при вращениибарабанчика 3 перемещается вдоль стержня. Величину перемещения можно отсчитать: целые миллиметра - по шкале p на стержне, десятые и сотые доли - по барабанчику 3. Фиксатор 2 служит для накалывания наблюдаемых точек на основу (план).

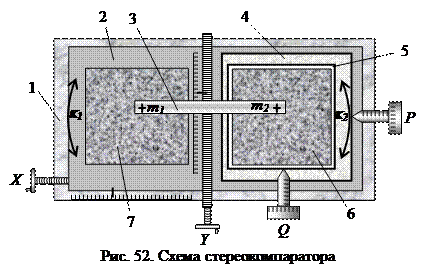
Прибором для измерения фотокоординат, продольного и поперечного параллаксов является стереокомпаратор (Рис. 52). Их конструкции различны (например, СК-2, или стереокомпаратор 1818 фирмы «Цейсс»), но принципиальные схемы одинаковы. Основными частями любого стереокомпаратора являются:

-

Станина 1 с двумя взаимно перпендикулярными направляющими X и Y (при измерении наземных снимков– Z);

- Основная каретка 2, перемещается вдоль направляющей X при вращении штурвала X. Величину перемещения можно определить по шкале X;

- Бинокулярная система 3 с марками m₁ и m_2, перемещается вдоль направляющей Y при вращении штурвала Y. Отсчет можно взять по шкале Y;

- Каретка продольных параллаксов 4 с винтом P, при вращении которого она перемещается вдоль оси X и который имеет шкалу для определения величины перемещения;

- Каретка поперечных параллаксов 5. При вращении винта Q она перемещается вдоль оси Y, и по его шкалеможно оценить величину перемещения;

- Снимкодержатели 6 и 7. Их можно вращать в своей плоскости винтами k₁ и k₂

У стереокомпаратора есть осветительная система, и регулировки, обеспечивающие настройку бинокулярной системы по глазному базису, по глазу и по предмету. Формы измерительных марок различны, но при увеличении они достаточно большие, и на рис. 53 стрелочками показано, какую их часть целесообразно использовать для точного наведения на измеряемую точку.

Отметим, что марки бывают светящиеся (в основном круглые) и несветящиеся. Несветящиеся марки имеют чёрный цвет, и на тёмных участках снимков измерения затрудняются. В большинстве приборов устанавливаются светящиеся марки. Цвет марки задаётся с помощью сменных фильтров – зелёный, красный, белый и т.д.

Процесс обработки снимков на стереокомпараторе включает: установку снимков в снимкодержателях, их ориентирование, определение мест нулей шкал прибора и непосредственно измерения. Следует помнить, что негативы устанавливаются эмульсией вниз, а диапозитивы – эмульсией вверх.

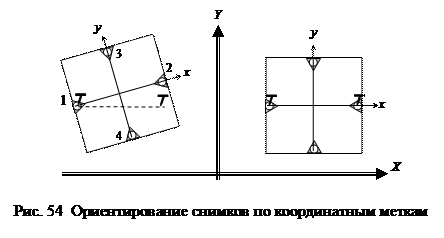
Снимок считается сориентированным, если его оси координат параллельны соответствующим направляющим стереокомпаратора (Рис. 54 правый снимок). В зависимости от способа введения системы координат на снимках, ориентирование выполняют по координатным меткам (основной вариант), тогда этот процесс независим для левого и правого снимков или по начальным направлениям. В первом случае действуют в такой последовательности:

1.

6. Основи визначення пари знімка. Кординати точки на стерео пари на аерофотознімки, повздовжні та поперечні паралакси.

Штурвалами X и Y, измерительную марку совмещают с координатной меткой 1;

2. Штурвалом X марку перемещают по направлению к координатной метке 2. Если она точно проходит через метку, значит снимок (правый на рис. 54) сориентирован.

3. Если марка оказалась выше или ниже, ее устанавливают на координатную метку 2, при этом половину перемещения осуществляют винтом k, а половину штурвалом Y.

4. Операцию ориентирования выполняют методом последовательных приближений.

При ориентировании правого снимка диапазон перемещения каретки по оси X может оказаться недостаточным, в таком случае действуют и винтом продольных параллаксов P.Допустимо также использовать винт поперечных параллаксов вместо штурвала Y. И, наконец, заметим, что иногда снимок ориентируют и по вертикальным меткам, если, например, качество их изображений выше, чем качество изображений меток 1 и 2.

После ориентирования приступают к процессу измерения снимков. Он состоит в том, что штурвалами X и Y совмещают измерительную марку с выбранной на левом снимке точкой а₁, а винтами P и Q, правую марку, совмещают с соответственной ей точкой а₂. Указанные операции являются монокулярными и в принципе, после их выполнения, можно брать отсчеты по шкалам стереокомпаратора. Но если рассматривать снимки двумя глазами возникнет стереоэффект, будет наблюдаться одна пространственная марка и точность наведения можно повысить, для чего:

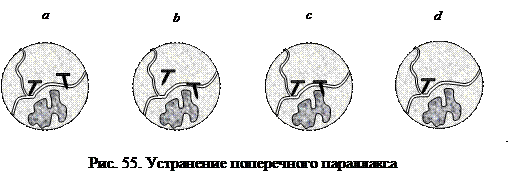
1. Вращением винта P пространственную марку «утапливают» и она раздваивается. В результате в плоскости изображения наблюдается одна из картин (рис 55). На картинкахa и b марки расположены на разной высоте (говорят, что наблюдается поперечный параллакс). Выполнять точные пространственные измерения в этом случае трудно и параллакс стараются устранить.

2.

Вращением винта поперечных параллаксов устраняют поперечный параллакс (картинка c).

3. Винтом продольных параллаксов приподнимают марку над точкой, а затем, вращая его в противоположном направлении, совмещают марку с точкой (картинка d), после чего и берут отсчеты по шкалам стереокомпаратора.

Пара горизонтальных снимков Р1и Р₂, полученных с горизон­тального базиса B = S1S2, с осями абсцисс, лежащими на одной прямой (идеальный случай съемки) в позитивном варианте, показа­на на рисунке 5.1.

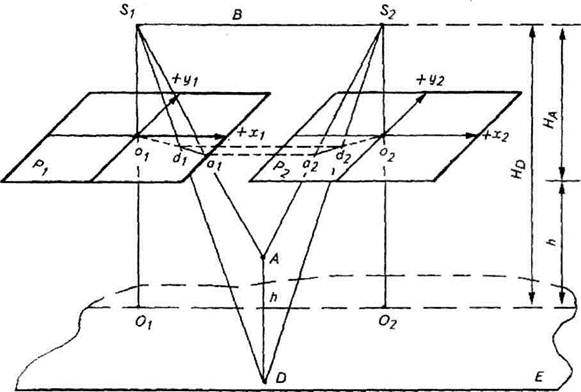
Рис. 5.1 - Изображение отвесной линии на паре снимков идеального случая съемки

Отвесная линия AD (на местности — столб, за­водская труба и т. п.) отобразилась на снимках отрезками а₁d₂ и a₂d₂, направленными соответственно в точки о_х и о₂, так как точки надира n1и п₂ на горизонтальных снимках совмещаются с главны­ми точками. Точки а₁ и а₂ будут иметь равные ординаты У а₁ =У а₂ так как в идеальном случае съемки след сечения снимков базис­ной плоскостью будет параллелен общему направлению осей абс­цисс этих снимков. Аналогичное равенство будет справедливым для любой пары соответственных точек.

Разность ординат соответственных точек пары снимков назы­вают поперечным параллаксом точки Y1 – Y2 = qt(1)

Одна и та же пара снимков в различных ракурсах показана на рисунках 5.1 и 5.2.

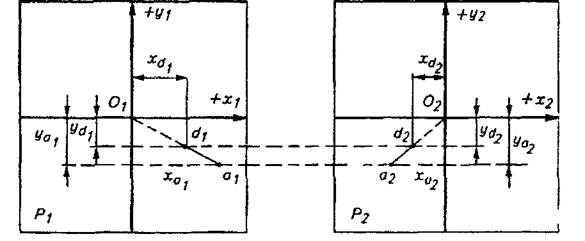
Рис. 5.2- Координаты концов отвесной линии, изображенной на паре снимков

Из них видно, что абсциссы точек изображения изменяются в зависимости от высоты их положения относительно плоскости, принятой за начальную (плоскость Е). С увеличением геодезической отметки точки масштаб изображения элементов, лежащих в горизонтальной плоскости, проходящей че­рез эту точку, будет укрупняться. Следовательно, через абсциссы точек пары снимков можно получить информацию о высотах то­чек и, в частности, о рельефе местности.

Разность абсцисс пары соответственных точек на левом и пра­вом снимках называют продольным параллаксом точки

P = X1 – X2(2)