Метод узловых потенциалов

Режим любой цепи полностью характеризуется уравнениями, составленными на основании первого и второго законов Кирхгофа, причем для определения токов во всех n ветвях необходимо составить и решить систему уравнений с n неизвестными.

Число уравнений, подлежащих решению, можно сократить, воспользовавшись методом узловых потенциалов, основанном на применении первого закона Кирхгофа и закона Ома.

Рассмотрим электрическую схему, приведенную на рис. 3.6.

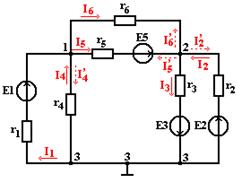
Рисунок 3.6

Пусть потенциал одного из узлов (например, узла 3) принят равным нулю, т.е. φ₃ = 0. Такое допущение не изменяет условий задачи, т.к. ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, к которым присоединена ветвь, а от разности потенциалов на зажимах ветви.

На основании первого закона Кирхгофа для узлов 1 и 2 этой схемы при выбранных положительных направлениях токов имеем:

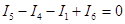; (3.38)

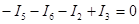. (3.39)

Токи в ветвях на основании закона Ома

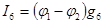; (3.40)

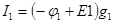; (3.41)

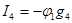; (3.42)

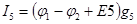; (3.43)

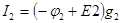; (3.44)

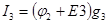, (3.45)

где φ₁ и φ₂ – потенциалы узлов 1 и 2.

После подстановки значений тока в уравнения (3.38) и (3.39) получим:

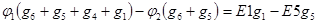; (3.46)

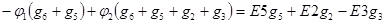, (3.47)

или

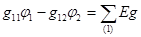; (3.48)

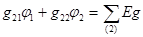, (3.49)

где g₁₁ = g₆ + g₅ + g₄ + g₁ – сумма проводимостей, присоединенных к узлу 1;

g₂₂ = g₆ + g₅ + g₂ + g₃ - сумма проводимостей, присоединенных к узлу 2;

g₁₂ = g₂₁ = g₅ + g₆ –сумма проводимостей ветвей, соединяющих эти узлы.

Правая часть каждого из уравнений (3.48), (3.49) равна алгебраической сумме произведений ЭДС источника на проводимость каждой из ветвей, которая присоединена к рассматриваемому узлу. Произведение вида Е*g записывается с положительным знаком в том случае, когда ЭДС направлена к рассматриваемому узлу, и с отрицательным, когда ЭДС направлена от узла.

Уравнения (3.48), (3.49) не зависят от выбранных положительных токов в ветвях (аналогичные уравнения могут быть получены, если направления токов на рис. 3.6 выбрать в соответствии с пунктирными стрелками).

Таким образом, можно написать уравнения для определения потенциалов узлов произвольной электрической цепи, не задаваясь положительными направлениями токов в ветвях; при этом потенциал одного из узлов следует принять равным нулю.

Если электрическая схема содержит не только источники ЭДС, но и источники тока, то в уравнения, составленные по первому закону Кирхгофа, войдут и токи источников тока. При составлении уравнений вида (3.48), (3.49) токи заданных источников тока учитываются для каждого узла в виде слагаемых в правой части, причем, как было отмечено ранее, с положительными знаками должны быть взяты токи источников тока, направленные к узлу, а с отрицательными – от узла.

Рассмотрим схему, приведенную на рис. 3.7.

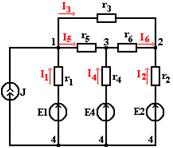
Рисунок 3.7

Для узлов 1, 2, 3 при φ₄ = 0 получим следующие уравнения:

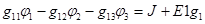; (3.50)

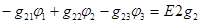; (3.51)

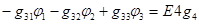, (3.52)

где

;

;

;

;

;

.

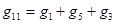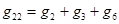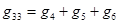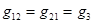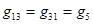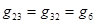Рассмотрим частный случай применения метода узловых потенциалов для частного случая с двумя узлами и произвольным числом активных ветвей, когда требуется определить напряжение между этими узлами.

Метод двух узлов

Пусть между узлами 1 и 2 включено m ветвей (рис. 3.8). Найдем напряжение U₁₂, записав уравнение для первого узла

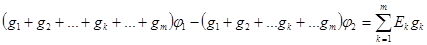. (3.53)

Тогда

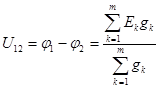. (3.54)

В полученном выражении числитель представляет сумму произведений ЭДС на проводимость всех ветвей, содержащих ЭДС (с положительным знаком берутся ЭДС, направленные к узлу 1), а знаменатель – арифметическую сумму проводимостей всех ветвей, включенных между узлами.

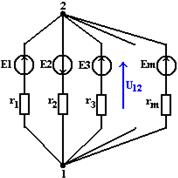
Рисунок 3.8

ЛИТЕРАТУРА

Основная

1. Касаткин В.С., Немцов М.В., Электротехника. - М.; Энергоатомиздат, 2000.

2. Основы промышленной электроники /Под ред. В.Г. Герасимова.- М.: Высшая школа, 1985.

3. Основы теории цепей; Учебник для ВУЗов. /В.П.Бакалов и др. 2-ое изд. перераб. и доп. – М.; 2000.

4. Сборник задач по электротехнике и основам электроники / Под ред. В.Г. Герасимова.- М.: Высшая школа, 1987.

5. Прянишников В.А. Электроника. - СПб; Корона принт, 2002.

6. Хоровиц П., Хилл У.. Искусство схемотехники.- М.:Мир, 1997.

7. Амочаева Г.Г. Электронный конспект лекций.

Дополнительная

1. Алексеенко А.Г., Шагурин Н.И. Микросхемотехника. Учебное пособие для вузов.- М.: Радио и связь, 1990.

2. Жеребцов И.П. Основы электроники.- Л.: Энергоатомиздат, 1990.

3. Попов В.П., Основы теории цепей.- Учебник для ВУЗов.- 3-е изд. испр.-М.: Высшая школа, 2000.

4. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench. в 2-х томах, Под ред. Д.И. Панфилова ДОДЭКА, 1999.-т.1-Электроника.

5. Электротехника/Ю.М. Борисов, Д.Н. Липатов, Ю.Н. Зорин. Учебник для вузов.- 2-е изд., перераб. и доп.- М.: Энергоатомиздат, 1985.

Лекция №3