Лекция 5. Системы автоматического регулирования. Задачи теории автоматического регулирования. Методы описания переходных процессов в САР
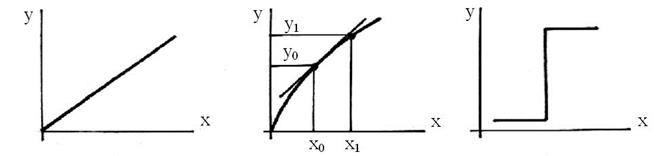
Задачей любой теории, направленной на решение вопросов проектирования технических устройств и систем, является создание формализованных математических моделей, в той или иной степени адекватных реальным механизмам, работающим в реальных условиях. Лишь в этом случае возможно проектирование с уверенностью, что изготовленная затем конструкция будет удовлетворять предъявляемым требованиям и давать желаемый эффект. Любые устройства и системы имеют два режима работы: статический и динамический (переходный), который происходит при перенастройке во время работы или как результат появления возмущений (изменение нагрузки, изменение окружающей среды и т. п.). Статический режим характеризуется статической характеристикой, т. е. зависимостью выходной величины от входной. Статические характеристики могут быть линейными, нелинейными, но линеаризуемыми при небольших отклонениях от рабочего режима заменой кривой касательной или секущей, и нелинейными, не поддающимися линеаризации, когда на характеристике имеется скачок, участки не зависимые от параметра входной величины и т. п. (рис. 47).
a) б) в)
Рис. 47. Статические характеристики: а – линейная; б – нелинейная линеаризуемая в окрестностях рабочей точки; в – нелинейная нелинеаризуемая
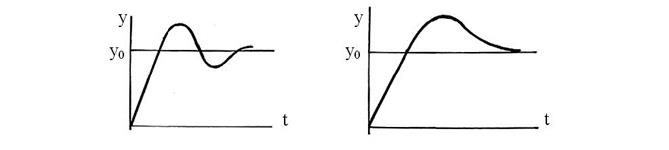
Переходный режим (иначе режим движения) характеризуется динамической характеристикой y = f(t) при изменении x(t) (рис. 48).
а) б)
Рис. 48. Динамические характеристики: а – с колебаниями; б – апериодическая
Если в динамической характеристике колебания затухают и у становится постоянным, то такая система называется устойчивой и пригодна к эксплуатации, если окончательное значение у имеет допустимую ошибку. Если колебания постоянны с постоянной амплитудой, то это системы с ограниченной устойчивостью, и эксплуатация их возможна, если размах амплитуд меньше допустимой ошибки. Если же величина отклонения от данного значения у с течением времени лишь увеличивается, то это – неустойчивые системы, и эксплуатироваться они не могут. Таким образом, до воплощения системы в реальную конструкцию необходимо знать, будет ли она устойчива в диапазоне возможных изменений параметров, а кроме этого, насколько точно и быстро будет устраняться ошибка. Исходя из этого исследование переходного процесса наиболее полно отражает работоспособность автоматической системы, и поэтому задачами теории автоматического регулирования (ТАР) являются:
– выбор схемы и параметров элементов системы, исходя из предъявляемых требований процесса - синтез;
– исследование САР с целью изучения характеристик ее рабочих процессов, т. е. устойчивости и качества регулирования (точности и быстродействия) – анализ.
Накопленный опыт создания автоматических систем, работающих в промышленности, показал, что структурная схема любой системы включает устройства с определенными функциями (см. рис. 4). Исходя из этого для технических систем задача синтеза сводится к задаче коррекции, т. е. выбору дополнительных элементов, включение которых в структурную схему обеспечит нужный запас устойчивости и требуемое качество регулирования.
Для решения задачи анализа необходимо исследовать переходные процессы, происходящие в системе. Согласно структурной схеме, появление возмущения вызывает изменение по входу каждого элемента. Таким образом, действуя на вход элемента или системы известным сигналом, можно получить переходную характеристику как одного элемента, так и всей системы. Для упрощения рассмотрения переходных процессов в ТАР работа системы в установившемся режиме до появления возмущения не рассматривается, что равносильно переносу начала координат на статической характеристике в точку, которая соответствовала предыдущему режиму до возмущения (рис. 49), т. е. исключаются из рассмотрения постоянные значения.
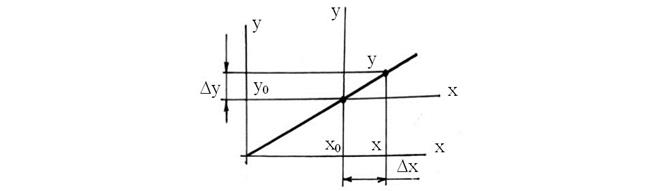
Рис. 49.Условия для рассмотрения переходного процесса: х0, у0 – параметры постоянного рабочего режима до возмущения; х, у – параметры режима после
возмущения
Так как по своему назначению САР препятствует отклонению от заданного режима, то изменение Δх и Δу не могут быть значительными и, таким образом, если статическая характеристика и нелинейна, то ее короткий отрезок можно заменить прямой (касательной или секущей) без существенной погрешности, т. е. линеаризовать. Поэтому, несмотря на то, что в реальной действительности нет линейных зависимостей, в ТАР нелинейные непрерывные характеристики линеаризуются, о чем уже говорилось ранее. Учитывая все вышеизложенное, переходный процесс может быть представлен некоторой функцией F(y,x, ỷ,ÿ) = 0, зависящей от у,х и их производных ỳ,ÿ и т. д. Функция F может быть записана с помощью степенного ряда Тейлора как линейное дифференциальное уравнение (правая часть линейна):
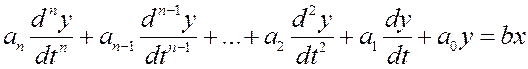 .
.
Здесь имеется в виду, что у и х – достаточно малые отклонения от первоначального значения, а коэффициенты 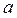 n – частные производные функции F:
n – частные производные функции F:
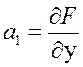 ;
; 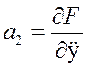 и т. д.
и т. д. 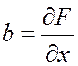
и являются постоянными (линейная зависимость – производные постоянны) для так называемых стационарных систем, таких, чьи параметры не зависят от времени (технические устройства) и определяются только конструкцией элементов. Поделив уравнение на 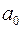 и имея в виду, что коэффициенты перед производными по времени есть постоянные времени, получим так называемое уравнение движения:
и имея в виду, что коэффициенты перед производными по времени есть постоянные времени, получим так называемое уравнение движения:
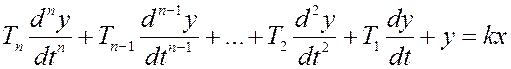 .
.
Если переходный процесс закончился, то все производные станут равны 0 и получаем линейную статическую характеристику у = kх. Коэффициент пропорциональности k, определяющий крутизну статической характеристики, называют коэффициентом усиления. Таким образом, для устройства, имеющего один вход и один выход, можно записать уравнение переходного процесса. Для анализа работы САР, учитывая принятое, система разбивается на динамические звенья, т. е. на устройства или узлы, входящие в них, имеющие один вход и один выход, поведение которых может быть описано с помощью линейных дифференциальных уравнений. При этом справедливым является принцип суперпозиции: результирующий эффект от нескольких независимых воздействий есть сумма эффектов, вызываемых каждым воздействием в отдельности. Исходя из этого можно рассматривать каждое динамическое звено отдельно и затем суммировать результат их поведения в переходном процессе, переходя к поведению всей системы.
Система, все звенья которой описываются линейными дифференциальными уравнениями, называется линейной. Если хотя бы одно звено системы нелинейно, то и вся система становится нелинейной и вышеизложенное к ней неприемлемо.
Анализ линейных САР производят следующим образом.
1. Расчленяют САР на динамические звенья.
2. Определяют статические характеристики каждого звена и, если они могут быть линеаризованы, то и всей системы.
3. Составляют уравнения динамики каждого звена.
4. Составляют динамическую структурную схему системы (связь отдельных звеньев) – графическое изображение уравнения движения системы.
5. Составляют общее уравнение динамики системы.
6. Анализируют уравнение, определяя устойчивость системы и качество регулирования.
Чтобы получить динамическую характеристику звена, и всей системы, необходимо решать дифференциальные уравнения. Решить дифференциальное уравнение – значит, найти такую функцию от заданного аргумента (в ТАР от t), которая удовлетворяет данному уравнению, т. е. при подстановке ее вместо у обращает это уравнение в тожество. Чтобы упростить составление общего дифференциального уравнения системы, в ТАР используют операторный метод, при котором функции времени заменяют соответствующими операторными изображениями. Операторное изображение дает возможность при составлении общего уравнения заменить операции дифференцирования и интегрирования на алгебраические действия. После получения общего уравнения в операторной форме можно перейти от изображения к реальной функции.
Операторным изображением функции времени f(t), которую называют оригиналом, является функция F(р) комплексной переменной 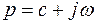
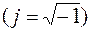 связанная с f(t) преобразованием Лапласа:
связанная с f(t) преобразованием Лапласа:
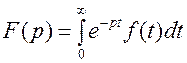 .
.
Преобразование Лапласа для типовых математических операций дается в виде таблиц в справочниках по математике. Обратное преобразование Лапласа :
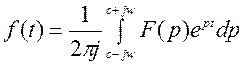 .
.
Эту формулу при анализе в TAP обычно не используют, а применяют другие способы. Практически же, чтобы записать дифференциальное уравнение в операторной форме преобразования Лапласа, нужно знак производной в дифференциальном уравнении заменить на символ оператора:
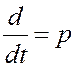 , тогда
, тогда 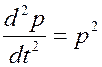 и
и  , а
, а 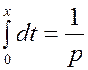 .
.
Оператор р рассматривается как число, которое можно подвергнуть алгебраическим действиям.
Запись дифференциальных уравнений дает возможность перейти к передаточным функциям, характеризующим звено и всю систему. Такой переход упрощает расчеты и не требует применения сложного математического аппарата. Дифференциальное уравнение в операторной форме звена или системы может быть представлено как: y(p) = W(p) х(p), где W(p) – передаточная функция оператора р .Часто запись упрощают, имея в виду все вышесказанное:
у = W(p)x.
Таким образом, чтобы найти W(p), необходимо разделить у на х. Например, для дифференциального уравнения второго порядка
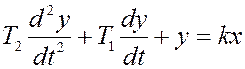
операторная формула 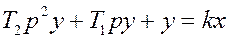 . Преобразуем:
. Преобразуем:
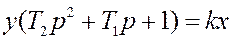
и находим передаточную функцию 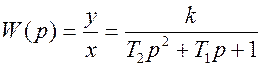 .
.
По передаточным функциям звеньев можно определить передаточную функцию всей системы, а затем уравнение движения.
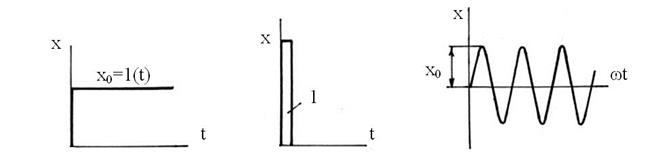
Реальные законы внешних воздействий, приложенных к системе, неизвестны, т. е. случайны. Поэтому в ТАР для анализа работы САР приняты типовые законы воздействия, имеющие место в реальных условиях: мгновенный скачок входной величины х (резкое увеличение нагрузки); синусоидальные колебания входной величины с постоянной амплитудой и изменяющейся частотой (вибрация); импульс бесконечно малой величины и бесконечно малой длительности (помеха). Если взять часть системы – звено, то можно любой сложный сигнал рассматривать через регулярные воздействия: единичное значение скачка (рис. 50, а), импульса, единичной амплитуды синусоидальных колебаний. Для линейных звеньев (правая часть дифференциального уравнения kx) переходную характеристику при регулярном скачкообразном воздействии x = x0 = 1(t) обозначают как h(t). Зная h(t) можно определить выходную величину у(t) при любом x(t) через интеграл Дюамеля (интеграл свертки в теории вероятности).
а) б) в)
Рис. 50. Регулярные воздействия: единичный скачок (a), импульс единичной
площади (б) и синусоидальные колебания с единичной амплитудой (в)
Единичный импульс δ(t) – дельта функция, 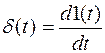 и
и
 – импульс единичной площади (рис. 50, б).
– импульс единичной площади (рис. 50, б).
Реакция звена y(t) на единичный импульс – импульсная переходная функция – используется при анализе нестационарных линейных систем.
Для анализа реакции звена и системы на периодический сигнал на вход подается регулярный сигнал y = y0sin 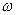 t при
t при 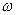 изменяющейся от 0 до
изменяющейся от 0 до 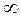 (рис. 50, в). То же в векторной форме:
(рис. 50, в). То же в векторной форме:
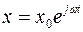 ,
,
где 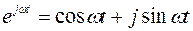 – комплексное число.
– комплексное число.
В результате на выходе звена сформируется сигнал 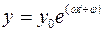
или 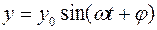 , т. е. синусоидальные колебания на выходе будут происходить с той же частотой при амплитуде у0 и отставанием по фазе на угол
, т. е. синусоидальные колебания на выходе будут происходить с той же частотой при амплитуде у0 и отставанием по фазе на угол 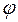 (рис. 51).
(рис. 51).
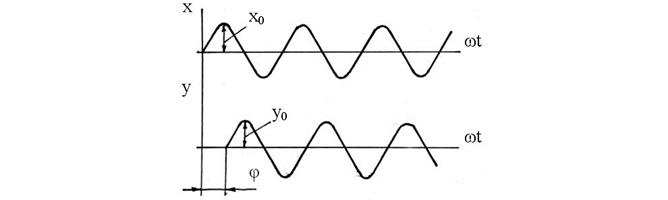
Рис. 51. Реакция звена на периодический сигнал
По мере увеличения частоты у0 будет уменьшаться, а угол 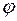 увеличиваться. Таким образом, можно построить амплитудную частотную характеристику
увеличиваться. Таким образом, можно построить амплитудную частотную характеристику 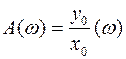 – АЧХ; фазовую чаcтотную характеристику
– АЧХ; фазовую чаcтотную характеристику 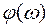 – ФЧХ и амплитудо-фазовую частотную характеристику АФЧХ – годограф, совмещающий обе эти характеристики. При построении АФЧХ
– ФЧХ и амплитудо-фазовую частотную характеристику АФЧХ – годограф, совмещающий обе эти характеристики. При построении АФЧХ 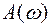 – длина вектора, а
– длина вектора, а 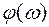 – угол наклона вектора к оси абсцисс (отрицательный, т. к. происходит отставание). Перейдя к векторной форме, годограф строят на комплексной плоскости, разделив действительную и мнимую части (рис. 52).
– угол наклона вектора к оси абсцисс (отрицательный, т. к. происходит отставание). Перейдя к векторной форме, годограф строят на комплексной плоскости, разделив действительную и мнимую части (рис. 52).
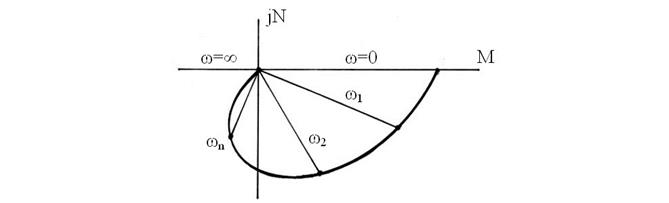
Рис. 52. Амплитудно-фазовая частотная характеристика
Представим связь между х и у при частотном воздействии в операторной форме как
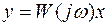 ,
,
где  – частотная передаточная функция звена.
– частотная передаточная функция звена.
Тогда 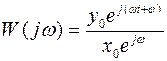 или
или  . В форме комплексного числа:
. В форме комплексного числа:
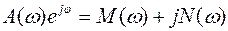 , а
, а 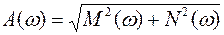 и
и 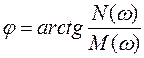 .
.
Для звеньев, которые описываются линейными дифференциальными уравнениями, существует однозначная связь между передаточной функцией 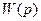 и
и 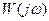 (через ряды Фурье). Для того, чтобы от
(через ряды Фурье). Для того, чтобы от 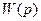 перейти к
перейти к 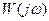 нужно p заменить на
нужно p заменить на 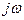 и в полученном выражении отделить действительную часть от мнимой.
и в полученном выражении отделить действительную часть от мнимой.
Построение и применение частотных характеристик упрощается при использовании логарифмических характеристик: амплитудно-частотной ЛАЧХ и фазочастотной. Для построения ЛАЧХ на оси абсцисс откладывают частоту 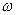 в декадах (10n), а по оси ординат – амплитуду в децибелах
в декадах (10n), а по оси ординат – амплитуду в децибелах 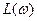 дБ.
дБ. 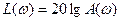 . Увеличение А(
. Увеличение А( 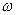 ) в 10 раз соответствует приращению L
) в 10 раз соответствует приращению L 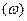 на 20 дБ. Для
на 20 дБ. Для  угол откладывают в градусах и в радианах. Так как при увеличении частоты угол становится все более отрицательным (и откладывается вниз), то обе характеристики совмещают по оси
угол откладывают в градусах и в радианах. Так как при увеличении частоты угол становится все более отрицательным (и откладывается вниз), то обе характеристики совмещают по оси 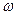 (рис. 53).
(рис. 53).

Рис. 53. Логарифмические частотные характеристики
Получить 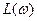 можно из
можно из 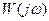 :
:
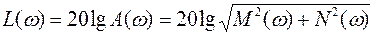 .
.
По логарифмическим частотным характеристикам чаще всего определяют поведение системы в переходном процессе. Логарифмическая характеристика 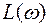 представляет собой прямые ломанные линии с наклоном, измеряемым в дБ/дек. Логарифмическая фазовая характеристика
представляет собой прямые ломанные линии с наклоном, измеряемым в дБ/дек. Логарифмическая фазовая характеристика  – кривая и строится по точкам, задаваясь
– кривая и строится по точкам, задаваясь 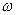 от 0 до
от 0 до 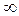 .
.
Дата добавления: 2016-03-22; просмотров: 2754;
