Лекция 6. Типовые динамические звенья систем автоматического регулирования

Как было показано в предыдущих лекциях, работоспособность САР можно определить, исследуя переходные характеристики системы и ее отдельных элементов. Таким образом, независимо от принципов работы и вида энергии, большинство применяемых технических устройств может быть сведено к относительно небольшому числу типовых динамических звеньев. Тип звена определяется дифференциальным уравнением движения, связывающим изменения выхода у от входного воздействия х. При принятом в ТАР скачкообразном регулярном воздействии получают дифференциальные уравнения для типовых звеньев с производной не выше второго порядка. Рассмотрим наиболее часто используемые для построения САР типовые звенья.

Пропорциональное звено (другие названия: идеальное, безынерционное).

При регулярном скачкообразном воздействии на вход этого звена появление выходного сигнала происходит мгновенно без инерции. Примером такого звена является электронный усилитель, потенциометр при мгновенном перемещении подвижного контакта на заданную величину, рычаг в механизмах и др.

Уравнения движения звена: у = kх.

Передаточная функция W(p) = у / х = k.

Форма h(t)-функции – скачок выходной величины у (рис. 54).

АФХЧ (годограф) – точка, с координатами 0; k (оператор в W(p) отсутствует), рис. 55.

ЛАЧХ и ФЧХ – прямые линии, рис. 56.

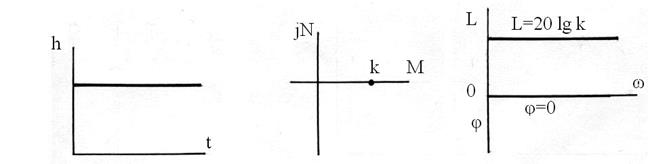
Рис. 54. Рис. 55. Рис. 56.

Апериодическое звено 1-го порядка (инерционное).

При воздействии на вход этого звена единичным скачком изменение у описывается дифференциальным уравнением 1-го порядка:

.

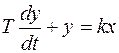Примером такого звена являются термопара (вход – температура, выход – термо-ЭДС), электродвигатель постоянного тока (вход – ток якоря, выход – частота вращения вала), печь или камера с тонкими стенками (вход – мощность источника нагрева, выход – температура), RC – цепи в электрических схемах и др. Постоянная времени Т в уравнении обусловлена массой, моментом инерции, индуктивностью, емкостью или другими параметрами устройства. Функция h(t) представляет собой экспоненту.

Для определения передаточной функции звена вводим оператор в дифференциальное уравнение:

.

Преобразуем:

.

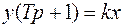Передаточная функция:

.

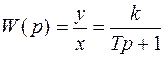Для определения АФЧХ заменяем p на 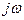, тогда

.

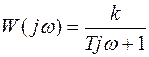Для разделения мнимой и действительной части умножаем числитель и знаменатель на :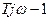

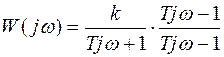, тогда .

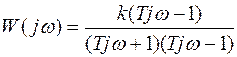В знаменателе разность квадратов преобразуем и делим числитель на знаменатель почленно:

.

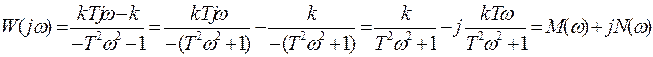Тогда

;

;

.

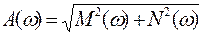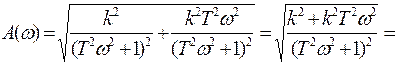
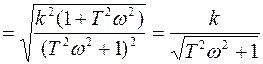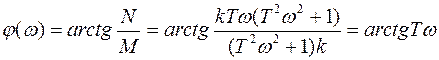По этим формулам можно построить АФЧХ, ЛАЧХ и ФЧХ. АФЧХ представляет собой половину окружности под осью действительных величин (рис. 57).

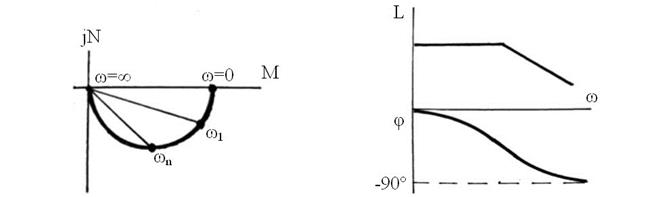
Рис. 57. Рис. 58.

Логарифмические характеристики определяют как

.

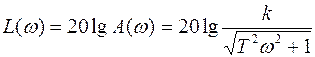Форма характеристик показана на рис. 58.

Решение дифференциального уравнения апериодического звена широко известно и представляет собой экспоненту

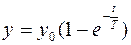, (1)

представленную на рис. 59.

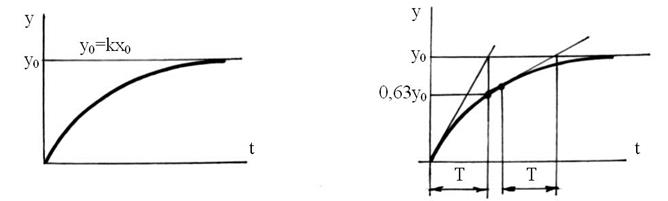
Рис. 59. Рис. 60.

Из выражения (1) следует, что у будет равен у₀ при t = ∞. Поэтому для практических расчетов считают, что у=у₀ при t = 4Т. Постоянная времени – это время, за которое у достиг бы у₀, если бы скорость его изменения была постоянна. При наличии экспериментально определенного переходного процесса для реального устройства, являющегося апериодическим звеном, постоянная времени Т может быть определена графически как проекция касательной из любой точки до пересечения с у₀ на ось времени (рис. 60). Обычно берут несколько точек и определяют среднее значение Т. Кроме этого, если в уравнении (1) t = Т, то у = 0,63у₀;

при t = 2Т у = 0.88у₀;

при t =3T у = 0,95у₀.

Отсюда также можно определить Т (рис. 60).

Для реального устройства параметры k и Т определены его конструкцией. Например, элемент системы стабилизации напряжения (см. рис. 5, а) обмотка электромагнита. Переходный процесс в обмотке при мгновенном скачке напряжения описывается уравнением Кирхгоффа:

,

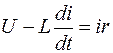где U – напряжение на нагрузке (скачок напряжения на выходе) генератора; L – индуктивность обмотки; i – ток в обмотке; r – активное сопротивление обмотки.

Перепишем выражение и поделим на r:

; .

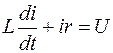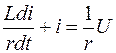Таким образом, можно считать, что L/r = T; 1/r = k; i =y; x = U;

т. е. получаем уравнение апериодического звена .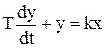

Если сопротивление r = 0,5 Ом, L = 1,5 мГн, тогда k = 1/0,5 = 2;
Т = 1,5∙10^-3/0,5 = 3 м/сек. Таким образом, можно построить реальные характеристики звеньев конкретного устройства.

Аналогично определяются характеристики других типовых динамических звеньев, которые сведены в табл. 3.

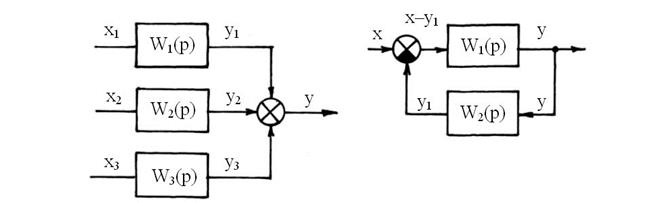
После нахождения передаточных функций всех звеньев системы составляется динамическая структурная схема. Динамическая структурная схема показывает взаимосвязь составных частей системы автоматического регулирования и характеризует ее свойства. Таким образом, динамическая структурная схема – это графическое условное изображение системы дифференциальных уравнений, записанных в операторной форме при нулевых начальных условиях. Каждое звено на схеме обозначают прямоугольником, внутри которого записывают передаточную функцию. Связь между звеньями обозначают стрелками, а место суммирования – окружностью, перечеркнутой диаметрами, образующими четыре сектора. Если производится вычитание (отрицательная обратная связь), то этот сектор зачерняется. Иногда вместо секторов в окружности ставят знак суммирования «+» или «–». Возможны три вида соединений звеньев: последовательное (рис. 61, а), параллельное (рис. 61, б) и параллельное со встречной передачей сигнала, т. е. с обратной связью (рис. 61, в).

а)

б) в)

Рис. 61.

Для последовательного соединения результирующая передаточная функция есть произведение передаточных функций звеньев:

.

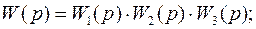
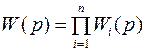Для параллельного соединения результирующая передаточная функция – сумма передаточных функций звеньев:

.

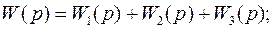
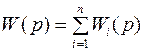Таблица 3

Пример устройства

Электронный усилитель, потенциометр

Электродвигатель, термопара, RC-цепь

Электрические емкость и индуктивность (вход – ток)

Дифференцирующие RCL-цепи

Электродвигатель с механизмом пере-мещения. Электри-ческие емкость и индуктивность (выход – напряжение)

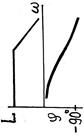
ЛАЧХ и ФЧХ

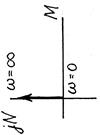
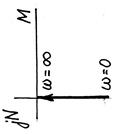
АФЧХ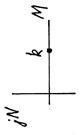

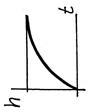
h(t)

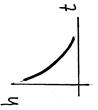
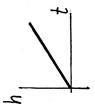
W(p)

k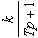

kp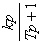

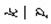
Тип звена и его дифференциальное уравнение

Пропорциональное у = kх

Апериодическое 1-го порядка

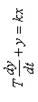
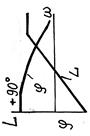
Дифференцирующее идеальное

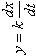
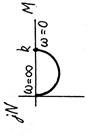
Дифференцирующее реальное

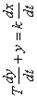
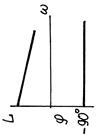
Интегрирующее идеальное

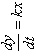
Окончание табл. 3

Пример устройства

Гидроцилиндр (выход – премешение с замедлением)

Электродвигатель с ощутимой массой якоря

RСL-цепи, уст-ройства с упругими элементами

Конвейеры; устройства, где точка контроля не совпадает с положением объекта

ЛАЧХ и ФЧХ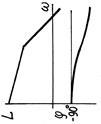

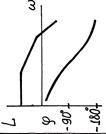
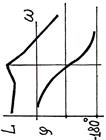
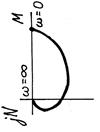
АФЧХ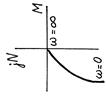

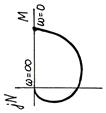
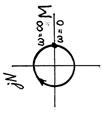
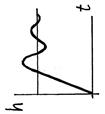
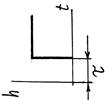
h(t)

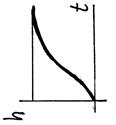
W(p)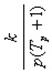

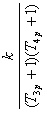
Ke-τp

Тип звена и его дифференциальное уравнение

Интегрирующее реальное

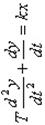
Апериодическое 2-го порядка 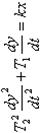При T1≥ 2T2 T22=T3T4, а T1 = T3 + T4 тогда

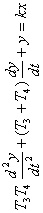
Колебательное 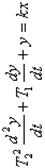При T1<2T2

Чистого запаздывания у = kx(t-τ)

Для определения W(p) отрицательной обратной связи (рис. 61, в) запишем связь входа и выхода звена 1 как

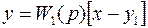. (2)

И для звена 2:

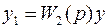. (3)

Подставляем формулу 3 в формулу 2 , исключая у₁:

.

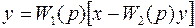Преобразуем:

; .

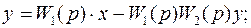
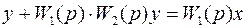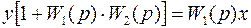Таким образом

.

где 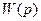– передаточная функция замкнутой системы. Если связь разомкнуть, то 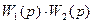– передаточная функция разомкнутой системы. Следовательно, передаточная функция замкнутой системы определяется как дробь, где в числителе передаточная функция звена прямой связи, а в знаменателе – единица плюс (отрицательная обратная связь, а если положительная, то минус) передаточная функция этой системы после размыкания.

Многие автоматические системы имеют многоконтурные структурные схемы. Большинство же методов расчета и анализа разработаны для одноконтурных систем. Приведение структурной схемы к одноконтурной производится методом эквивалентного преобразования. Эти методы рассматриваются в литературе, предназначенной для более глубокого изучения ТАУ.