Уравнение Михаэлиса-Ментен
Теперь обратимся к кинетике каталитических реакций. Для определенности, будем иметь в виду ферментативные реакции, хотя многое из нижеследующего справедливо и для прочих каталитических процессов.
 |
1. Как и для цепных реакций, уравнение скорости ферментативного процесса зависит от его конкретного механизма. Рассмотрим простейший случай: односубстратныв необратимые реакции вида
протекающие в две стадии:
 |
На первой (обратимой) стадии образуется фермент-субстратный комплекс ES, а на второй он необратимо распадается на фермент и продукт реакции.
2. Вывод уравнения скорости производится по тому же принципу, что и для
цепных реакций (п. 20.2).
а) Так, тоже исходят из условия стационарности. В данном случае оно означает постоянство концентрации комплекса ES:
 |
б) Заметим, что концентрация свободного фермента равна
 |
где cE,0 — общая концентрация фермента — и в свободном состоянии, и в составе комплекса ES.
 |
в) Подставляя cEв (20.29), можно найти стационарную концентрацию комплекса:
 |
Здесь введена константа Михаэлиса:
 |
г) Скорость же образования конечного продукта, а значит и скорость реакции в целом, очевидно, такова:
 |
д) Подставляя cES, получаем искомое выражение:
Величина Vmax — это максимальная скорость реакции; формула же (20.34, а) — уравнение Михаэлиса—Ментен, являющееся основным в ферментативной кинетике.
3. Проанализируем это уравнение.
 |
а) При малых концентрациях субстрата S (когда cS« KM) имеем:
т.е. фермент работает в линейном режиме, а реакция имеет первый порядок.
б) Если же, напротив, концентрация субстрата очень велика, получаем режим насыщения:
Здесь скорость перестает зависеть от концентрации субстрата, не поднимаясь выше Vmax, т.е. реакция приобретает нулевой порядок.
в) Отсюда — та гипербола, которой описывается зависимость v от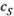 
для ферментативной реакции (рис. 20.3). По мере же расходования субстрата порядок реакции изменяется от нулевого до первого.
Дата добавления: 2016-03-20; просмотров: 561;