Буферное действие растворов слабых электролитов
1. а) Для понимания сути буферного действия рассмотрим построенный на
рис. 12.1график титрования слабой кислоты сильной щелочью. Заметим, в качестве слабой кислоты можно рассматривать любую сопряженную слабую кислоту, в том числе, например,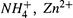 
и т.д.
б) На таких графиках по горизонтальной оси обычно откладывают рН, а по вертикальной оси — молярную концентрацию эквивалента добавляемой щелочи в рассматриваемом растворе, обозначенную с(В).
в) Не следует забывать, что здесь первичным является добавление щелочи, а вторичным — изменение (в связи с этим) рН.
2. Итак, допустим, что имеется чистый раствор слабой кислоты с pH0,, к которому добавляется щелочь, т.е. увеличивается с(В).
а) Пока не будет достигнут рН и рКа — 1,5, слабая кислота практически вся находится внедиссоциированном состоянии и не влияет на рН. Поэтому до
данного уровня изменение рН происходит быстро.
б) Но по достижении указанного значения рН начинается заметная диссоциация слабой кислоты:
 |
Образующиеся протоны будут связывать бóльшую часть добавляемых гидроксильных ионов, и изменение рН станет гораздо более медленным,хотя
совсем не прекратится.
в) В этом-то и состоит буферное действие слабых электролитов: их присутствие препятствует резкому изменению рН при добавлении щелочных или
кислотных соединений, а при непрерывном добавлении последних — снижает
скорость изменения рН.
Зона же рКа±1,5 называется зоной буферного действия слабого электролита. (Иногда за таковую принимают более узкий интервал — рКа± 1.) Продолжающееся добавление щелочи, хотя и медленно, но повышает рН среды.
г) Когда рН выходит за верхнюю границу буферной зоны, буферное действие
прекращается. К этому времени практически весь слабый электролит переходит в форму сопряженного основания (R) и перестает реагировать на дальнейшее повышение рН, в связи с чем рН вновь начинает быстро возрастать.
3. а) Если теперь (после достижения высокого уровня рН) начать добавлять
сильную кислоту, то все будет происходить в почти обратном порядке. «Почти» — оттого, что вначале некоторое количество кислоты потребуется на нейтрализацию избытка щелочи.
б) Затем (при дальнейшем добавлении кислоты) вначале будет наблюдаться
быстрое снижение рН, затем (в зоне буферного действия слабой кислоты) —
медленное, а после выхода из этой зоны — опять быстрое понижение рН.
12.2. Расчет рН раствора с буферной системой
1. а) Заметим: в зоне буферного действия слабой кислоты в растворе присутствуют два компонента — сама кислота и ее соль с сильным основанием:
RH ↔ R + H+
сопр. к-та сопр. осн. . (12.1,a-б)
BR → B+ + R
б) Поэтому, если хотят составить уже готовую буферную систему, в раствор вносят два вещества:
I. либо, как в (12.1), слабую кислоту и её соль с сильным основанием,
II. либо слабое основание и его соль с сильной кислотой.
2. Поясним ещё раз, почему необходима соль.
а) В её отсутствие имелся бы чистый раствор слабого электролита, а в таком растворе, как было видно из оценок (11.29,а-б), степень диссоциации очень низка и рН находится вне зоны буферного действия (точка рН0 на рис.12.1). Поэтому при внесении в раствор, например, сильной кислоты получился бы сильный скачок в кислую сторону.
б) В присутствии же соответствующей соли сразу устанавливается рН, находящийся в пределах буферной зоны.
 |
3. а) Чтобы рассчитать это значение рН, будем исходить из уравнения:
которое связывает рН с равновесными концентрациями двух форм слабого
электролита.
б) Обратимся к системе (12.1). В первом уравнении данной системы в чистом
растворе слабой кислоты равновесие резко сдвинуто влево, а в присутствии
соли, т.е. дополнительных частиц R, оно еще более сдвигается влево. Поэтому
 |
 |
где с0(соль) и с0(кислота) — общие концентрации компонентов буферной
системы. В итоге для буферной системы получаем уравнение Гендерсона—
Хассельбаха:
которое в отличие от формулы (11.19, б) является приближенным.
в) Таким образом, значение рН буферной системы определяется отношением
концентраций соли и слабой кислоты. А поскольку при разбавлении раствора
это отношение не меняется, то не меняется при разбавлении и рНбуферной системы. Это отличает ее от чистого раствора слабого электролита, для которого справедлив закон разведения Оствальда (п. 11.4).
4. а) Если речь идет о буферной системе типа II (слабое основание и его соль с сильной кислотой), то химические уравнения таковы:
ВОH ↔ В + ОH–
сопр.осн. сопр.к-та (12.4)
BА → B + А–
 |
б) Уравнение (11.19,б) принимает вид:
 |
причем
 |
в) Это дает следующее уравнение Гендерсона-Хассельбаха:
5. Пример – ацетатный буфер, т.е. смесь уксусной кислоты (рКа = 4,76) и ацетата Na.
 |
а) Допустим, нужен раствор с рН = 5,0. Тогда из уравнения (12.3) находим:
В таком соотношении для получения заданного значения рН надо смешивать компоненты системы.
б) Теперь пусть приготовлен буфер именно с указанным отношением концентраций, причем конкретные значения последних таковы:
 |
К раствору добавлен NaOH до с(В) = 0,01 М.
 |
I. В отсутствие буфера это привело бы к резкому увеличению рН среды:
Таким образом, если бы изначально была чистая вода (рН = 7,0), то рН увеличился бы на 5 единиц.
 |
II. Наличие же буферной системы приводит к следующему результату: добавление NaOH стимулирует диссоциацию соответствующего количества слабой кислоты, так что концентрация соли в буферной системе возрастает, а концентрация кислоты — уменьшается:
 |
Отсюда новое значение рН равно:
т.е. по сравнению с исходным значением (5,0) рН изменился всего на шесть сотых единицы. Это — наглядная демонстрация буферного действия.
Дата добавления: 2016-03-20; просмотров: 1526;