Растворимость твердых веществ в жидкости
А как зависит от температуры растворимость твердого вещества? Подход
и принципиальные результаты здесь совершенно таковы же, что и для газов.
а) Воспользуемся формальным представлением растворения в виде химической реакции:
(Вещество 2)тв ↔ (Вещество 2)р-р (8.10,а)
б) Как известно, константа равновесия в данном случае просто совпадает
с равновесной концентрацией растворяемого вещества:
Кр = [Вещество 2] . (8.10,б)
 |
в) Для этой константы-концентрации уравнение изобары (5.20) записывается так:
 |
г) Вытекающий из него вывод аналогичен таковому для растворимости газов:
если
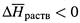 , то при росте температуры растворимость вещества понижается. Однако в случае твердых веществ чаще наблюдается обратная ситуация:
, то при росте температуры растворимость вещества понижается. Однако в случае твердых веществ чаще наблюдается обратная ситуация:
Поэтому их растворимость при нагревании обычно увеличивается.
Краткое содержание главы 8
Глава посвящена частному виду двухкомпонентных систем – РАСТВОРАМ.
1. Для их характеристики наиболее часто используются молярные (сi) и моляльные (bi) концентрации, а также молярная доля (Хi), связанные следующими соотношениями:
сi ≈ Xi ni /Vo , Xi ≈ bi Mi
2. В т.н. ИДЕАЛЬНЫХ РАСТВОРАХ все межмолекулярные взаимодействия одинаковы по характеру и силе. Для таких растворов изменение энергии Гиббса составляет:
а) при образовании газового раствора –
ΔGо = (n1 + n2) RT [X1ln X1 + X2ln X2] ,
б) в жидких растворах – при повышении концентрации растворённого вещества с X2 до X2′:
ΔGо = n1 RT ln ( X1′ /X1 ) + n2 RT ln ( X2′ /X2 ) + Δn2 RT ln X2′ .
 3. Затем речь шла о ФАЗОВОМ РАВНОВЕСИИ МЕЖДУ РАСТВОРИТЕЛЕМ И ЕГО ПАРОМ над раствором. Был сформулирован ЗАКОН РАУЛЯ: давление насыщенного пара над ИДЕАЛЬНЫМ раствором пропорционально молярной доле растворителя:
3. Затем речь шла о ФАЗОВОМ РАВНОВЕСИИ МЕЖДУ РАСТВОРИТЕЛЕМ И ЕГО ПАРОМ над раствором. Был сформулирован ЗАКОН РАУЛЯ: давление насыщенного пара над ИДЕАЛЬНЫМ раствором пропорционально молярной доле растворителя:
 4. Отсюда вытекают КОЛЛИГАТИВНЫЕ ЭФФЕКТЫ. Растворение вещества в растворителе приводит к:
4. Отсюда вытекают КОЛЛИГАТИВНЫЕ ЭФФЕКТЫ. Растворение вещества в растворителе приводит к:
а) понижению давления насыщенного пара растворителя,
б) понижению температуры замерзания раствора,
в) повышению температуры кипения,
г) возникновению осмотического давления,
 При этом эбулиоскопическая и криоскопическая константы определяются природой только растворителя:
При этом эбулиоскопическая и криоскопическая константы определяются природой только растворителя:
5. Для растворов ЭЛЕКТРОЛИТОВ вводится поправочный множитель — ИЗОТО-НИЧЕСКИЙ КОЭФФИЦИЕНТ i :

причем для сильных и для слабых электролитов он вычисляется так:
 |
6. а) И в общем случае эффективные концентрации (АКТИВНОСТИ) часто отличаются от истинных:
аX = γХ , аc = γс , ab = γb .
б) КОЭФФИЦИЕНТЫ АКТИВНОСТИ γ зависят от концентрации веществ, что выражается УРАВНЕНИЕМ ГИББСА-ДЮГЕМА:
(1 – Х2) d (ln γ1) = – X2 d (ln γ2) .
7. РАСТВОРИМОСТЬ ГАЗА зависит от его парциального давления над раствором (ЗАКОН ГЕНРИ) и концентрации солей в растворе (ЗАКОН СЕЧЕНОВА):
с2 ≈ КР Р2 , ln KР = ln KР0 – k cсоль .
Глава 9. ЖИДКИЕ СМЕСИ С НЕОГРАНИЧЕННОЙ
РАСТВОРИМОСТЬЮ КОМПОНЕНТОВ
Теперь рассмотрим растворы жидкости в жидкости, которые правильней называть смесями. Смеси различаются по взаимной растворимости жидкостей, что связано с природой последних и характером межмолекулярного взаимодействия.
Рассмотрим вначале простейший тип смесей. Как обычно, будем иметь в виду систему под поршнем.
9.1. Смеси, подчиняющиеся закону Рауля (идеальные смеси): давление и состав пара
1. Исходные условия. а) Будем также считать, что жидкости
I. неограниченно растворимы друг в друге и
II. обе являются летучими, т. е. дают над раствором пар.
б) Введём обозначения: 1 — менее летучая жидкость, 2 — более летучая, т.е. у первой жидкости — ниже давление насыщенного пара над чистым веществом и, соответственно, выше температура кипения:
 |
в) Вспомним также условие идеальности раствора, согласно которому все виды межмолекулярных взаимодействий в системе — 1–1, 2–2 и 1–2 — одинаковы
по характеру и силе. Примерами являются смеси близких по природе жидкостей: бензол–толуол, гексан–гептан, метанол–этанол.
2. а) Для идеальной смеси закон Рауля (8.12) применим к обоим летучим компонентам:
 |
откуда

 б) Получается, что общее давление пара над смесью линейно зависит от состава смеси. Это изображено на рис. 9.1, где
б) Получается, что общее давление пара над смесью линейно зависит от состава смеси. Это изображено на рис. 9.1, где
- по оси абсцисс отложена молярная доля в жидкой фазе более летучего компонента,
- пунктирными линиями показаны парциальные давления паров каждого из двух
компонентов (при разном составе смеси)
- и сплошной линией — общее давление
пара над раствором.
3. а) Нетрудно определить состав пара при том или ином составе жидкой фазы. Молярные доли каждого вещества в паре обозначим штрихом. Тогда, например, доля в паре второго компонента такова:
 |
 Последнее выражение получено путем деления числителя и знаменателя на
Последнее выражение получено путем деления числителя и знаменателя на 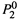 , а ζ1— величина, меньшая единицы:
, а ζ1— величина, меньшая единицы:

поскольку, в соответствии с условием, первый компонент является менее летучим.
 |
б) Заметим: так как X1 + X2 = 1, то знаменатель выражения (9.4, в) меньше единицы:
в) Таким образом, доля второго (более летучего) компонента в паре выше, чем в жидкой смеси. В этом заключается первый закон Коновалова: по сравнению с жидкой фазой, состав газовой фазы обогащен более летучим компонентом.
На рис. 9.2 это выражается в том, что кривая зависимости 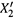 от X2 идет выше диагонали единичного квадрата. График же данной зависимости нетрудно построить, используя формулу (9.4, в).
от X2 идет выше диагонали единичного квадрата. График же данной зависимости нетрудно построить, используя формулу (9.4, в).
9.2. Идеальные смеси:
полный вариант диаграммы давления
 1. а) Нередко на диаграмме давления (рис. 9.3), кроме зависимости P0 от состава жидкости X2 (линии ж), изображают также линию, связывающую P0
1. а) Нередко на диаграмме давления (рис. 9.3), кроме зависимости P0 от состава жидкости X2 (линии ж), изображают также линию, связывающую P0
с составом газовой фазы 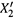 (линия п). Для этого удобно ввести еще одну
(линия п). Для этого удобно ввести еще одну
координатную ось — 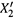 (хотя часто обходятся и без неё).
(хотя часто обходятся и без неё).
б) Тогда построение таково (см. рис. 9.3). Для произвольного значения X2,М по формулам (9.4) рассчитывают соответствующее значение 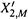 (большее X2,М) и находят точку пересечения этой ординаты
(большее X2,М) и находят точку пересечения этой ординаты 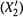 с изобарой, проходящей через точку М. Тем самым получают точку М', принадлежащую линии п.
с изобарой, проходящей через точку М. Тем самым получают точку М', принадлежащую линии п.
2. Линиями ж и п диаграмма разделяется на три области.
а) Над линией ж система имеет только жидкую фазу (имеется в виду, что система находится под поршнем). В любой точке этой области внешнее давление (создаваемое поршнем) больше возможного давления пара смеси, так что пар не образуется.
б) Между линиями возможно существование двух фаз: и жидкой, и газообразной. Например, в точке О (состав — X2,0, внешнее давление — P0 = Pм) сосуществуют жидкая фаза с составом X2,М и газовая с составом 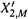 .
.
в) А под линией n система имеет только одну газовую фазу.
3. Отметим также, что состав газовой фазы зависит от температуры {закон
Вревского). Это следует из формулы (9.4,в). В ней фигурирует ζ1 — отношение
величин 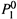 и
и 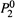 . Если эти величины с ростом температуры изменяются
. Если эти величины с ростом температуры изменяются
непропорционально, то 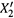 оказывается функцией температуры.
оказывается функцией температуры.
9.3. Идеальные смеси: диаграммы кипения
1. Теперь обратимся к температуре кипения смеси.
а) Если компоненты смеси различаются по своей летучести (значениям 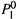 и
и 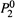 ), то они различаются и по температурам кипения в чистом состоянии.
), то они различаются и по температурам кипения в чистом состоянии.
б) У менее летучей жидкости 1, очевидно, данная температура выше:
 |
Это показано на рис. 9.4 соответствующими точками на осях температуры.
2. Для смеси же температура кипения,как тоже очевидно, будет зависеть от её состава.
а) Понятно, что с ростом X2 (увеличением доли более летучего компонента) Тксмеси будет уменьшаться — от Тк,1 до Тк,2 (нижняя кривая на рис. 9.4).
 б) В отличие от зависимости P0(X2) ((9.3) и рис. 9.1), рассматриваемая сейчас зависимость является нелинейной.
б) В отличие от зависимости P0(X2) ((9.3) и рис. 9.1), рассматриваемая сейчас зависимость является нелинейной.
Действительно, количественную зависимость Тк от X2 можно получить, если исходить из условия: общее давление пара над смесью равно внешнему давлению:
 |
 |
где для величин
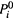 следует использовать уравнение Клаузиуса-Клайперона (7.22,6) с искомой температурой:
следует использовать уравнение Клаузиуса-Клайперона (7.22,6) с искомой температурой:
Без дальнейших вычислений понятно, что
зависимость Тк от Х2 окажется нелинейной.
в) Верхняя кривая (п) связывает температуру кипения и состав газовой фазы. Построение ее происходит так же, как построение линии п на рис. 9.3; так что в итоге точке М линии ж соответствует точка М' линии п.
3. а) Диаграмма опять-таки разделяется на три области, но в отличие от диаграммы давления порядок расположения областей обратен: область пара — над линией п, а область жидкой фазы — под линией ж.
б) Кроме того, диаграмма позволяет прогнозировать, как будут изменяться состав и масса каждой фазы в процессе кипения смеси.
4. Состав фаз. Пусть исходный состав жидкости (находящейся в системе под поршнем) — X2,0.
а) По достижении температуры кипения (точки М на нижней кривой диаграммы рис. 9.4) в системе начинает образовываться пар с составом 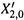 (точка М' на верхней кривой).
(точка М' на верхней кривой).
б) В процессе кипения переход в пар второго (более летучего) вещества происходит легче, чем первого. Поэтому содержание второго компонента в жидкой фазе (величина X2) неуклонно снижается. Движение идет по нижней кривой влево от точки М.
в) Соответственно, снижается содержание этого вещества и в паре. Движение по верхней кривой от точки М' — тоже влево.
г) Таким образом, на первых стадиях процесса преимущественно испарялся компонент 2 и пар был им обогащен. Со временем же постепенно возрастают:
- доля компонента 1 в жидкой фазе,
- температура кипения этой фазы,
- доля компонента 1 в паре.
д) Напомним: предполагается, что пар никуда из системы не отводится. Тогда суммарный состав системы (с учетом и жидкости, и пара) остается постоянным: он численно равен X2,0 и на рис.9.4 отражается одной из точек вертикали МN.
е) Ясно также, что при полном испарении обоих компонентов состав пара будет описываться точкой N, т.е. сравняется с составом исходной жидкой смеси.
5. Масса фаз. Кроме состава фаз смеси на разных стадиях испарения, можно оценить и массы фаз.
а) Допустим, на некоторой стадии кипения состав жидкой фазы отражается
точкой К, а парообразной — точкой К', тогда суммарное состояние системы
отражается точкой О (местом пересечения горизонтали КК' с вертикалью МN).
б) Можно убедиться в перекрёстном правиле рычага:
- отрезок ОК на рис. 9.4, примыкающий к нижней кривой (ж), пропорционален массе газовой фазы,
- а отрезок ОК', примыкающий к верхней кривой (п), — массе жидкой фазы.
в) Действительно, в состоянии О молярная доля вещества 2 в системе
(сохраняющая исходное значение) может быть вычислена так:
 |
где n0 — общее число молей обоих компонентов в обеих фазах, а nж и nг —
количество молей обоих компонентов, соответственно, в жидкой и газовой фазах.
 |
Подставляя n0 = nж + nг , после простых преобразований получаем:
что и означает правило рычага.
Дата добавления: 2016-03-20; просмотров: 1006;
