Единичный скачок и ступенчатое воздействие
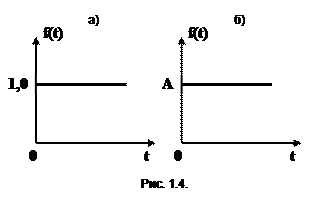
Математически единичный скачок (рис 1.4,а) можно выразить следующим образом:
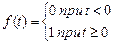
Ступенчатое воздействие (рис 1.4,б)
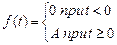
 Воздействиям такого рода соответствуют, например, набросы и сбросы нагрузки, включение или снятие напряжения и т.п.
Воздействиям такого рода соответствуют, например, набросы и сбросы нагрузки, включение или снятие напряжения и т.п.
Единичный импульс
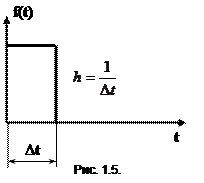
Единичный импульс – это воздействие бесконечно большой величины h и бесконечно малой длительности ∆t при условии, что
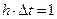 .
.
Следовательно, единичный импульс представляет собой математическую идеализацию предельно короткого импульсного сигнала, площадь которого равна 1 при длительности равной нулю и высоте, равной бесконечности.
3. Импульсное воздействие
Импульсное воздействие представляет собой воздействие бесконечно большой величины H и бесконечно малой длительности ∆t при условии, что
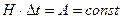
Единичный импульс и импульсное воздействие реализовать практически невозможно, их можно осуществить только приближенно. Для импульсов прямоугольной формы с длительностью 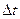 амплитуда единичного импульса будет равна
амплитуда единичного импульса будет равна 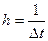 , а амплитуда импульсного воздействия
, а амплитуда импульсного воздействия 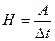 . Т.е. единичный импульс (импульсное воздействие) можно рассматривать как предел прямоугольного импульса длительностью
. Т.е. единичный импульс (импульсное воздействие) можно рассматривать как предел прямоугольного импульса длительностью 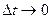 и высоты
и высоты 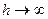
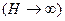 при сохранении указанных выше условий.
при сохранении указанных выше условий.
Предельный единичный импульс называют 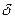 – функцией. Импульсная функция может быть рассмотрена как производная от ступенчатого воздействия.
– функцией. Импульсная функция может быть рассмотрена как производная от ступенчатого воздействия.
При подаче на вход какого-либо звена или системы единичного ступенчатого воздействия его выходная величина изменяется во времени. График изменения выходной величины в данном случае будет представлять переходную или временную функцию 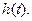
При подаче же на вход единичного импульса получаем импульсную переходную характеристику или весовую функцию (функцию веса), обозначаемую 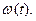
Дельта – функция связана с единичным ступенчатым воздействием (функцией) выражением
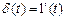
Отсюда следует аналогичная связь между переходной и весовой функциями линейных звеньев
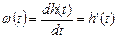
и наоборот
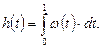
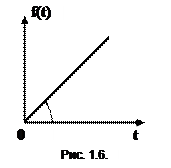
4. Линейное воздействие (рис 1.6.) – это воздействие, которое изменяется по линейному закону
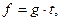
где 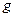 – угловой коэффициент прямой.
– угловой коэффициент прямой.
|
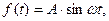
|
|
|
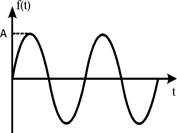
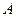 – амплитуда;
– амплитуда;
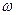 – круговая частота.
– круговая частота.
|
Дата добавления: 2016-03-20; просмотров: 3720;
