Правило большинства голосов

Несколько изменим результаты голосования, чтобы избежать парадокса Кондорсе:

Число голосовавших	Предпочтения

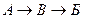
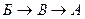
Можно подсчитать, что при этих результатах по принципу Кондорсе был бы избран кандидат 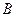, который при попарном сравнении побеждает двух других кандидатов. Однако если мы используем принцип выбора на основе большинства голосующих, то победителем будет кандидат 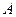, но при этом он не набрал абсолютного большинства голосов.

Метод Борда

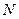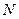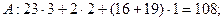
Согласно этому методу, результаты голосования выражаются в виде числа баллов, набранных каждым из кандидатов. Пусть число кандидатов равно . Тогда за первое место присуждается баллов, за второе – баллов и т. д. За последнее место присуждается 1 балл. Применим метод Борда к рассматриваемому случаю: подсчитаем число баллов кандидатов: . Таким образом, побеждает кандидат .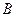

Однако при использовании данного подхода также возможны проблемы. Пусть результаты голосования представлены в следующей таблице:

Число голосовавших	Предпочтения

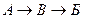
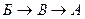
Подсчитав баллы по правилу Борда, находим: 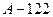балла; 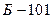балл; 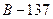баллов. В соответствии с полученными результатами победителем следует объявить кандидата 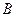. Однако в данном случае явным победителем является кандидат 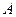, набравший абсолютное большинство голосов ( + 1 голос).

Приведенные примеры показывают, что парадоксы при голосовании не возникают лишь в случае, когда есть 2 кандидата и победитель определяется по принципу абсолютного большинства голосов. Однако такой случай нетипичен для большинства реальных ситуаций. Замечено, что парадоксы сохраняются и при введении двух туров выборов (при условии, что во второй тур выходят 2 кандидата, набравшие максимальное число голосов в первом туре). Рассмотрим первый пример (п. 1, парадокс Кондорсе). В соответствии с предпочтениями голосующих, во второй тур выходят 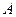(23 голоса) и 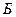(19 голосов), после чего побеждает 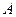. Однако при небольшом усилении первоначальной позиции 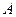предпочтения двух избирателей в третьей строке таблицы изменятся на 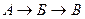, и во второй тур выходят 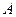(25 голосов) и 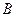(18 голосов), после чего побеждает .

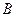Пусть имеется 2 коалиции: «черные» (8 человек) и «белые» (19 голосов). Возможна следующая многоступенчатая система голосования: