Принятие решений в условиях риска
Принятие решений в условиях риска характеризуется тем, что поведение среды имеет случайный характер, причем в этой случайности имеются закономерности стохастического типа. В общем случае это проявляется в том, что существует некоторая вероятностная мера, в соответствии с которой возникают те или иные состояния среды. Причем ЛПР имеет определенную информацию об этом. В наиболее простом случае это выглядит так: если множество состояний среды 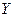 конечно, то есть
конечно, то есть 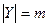 , то вероятностная мера на нем может быть задана вероятностным вектором
, то вероятностная мера на нем может быть задана вероятностным вектором  , где
, где 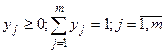 ,
,  – вероятность наступления
– вероятность наступления 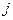 -го состояния среды.
-го состояния среды.
Считаем, что оценочная структура ЗПР задана в виде оценочной функции. Целевая функция представлена в виде матрицы выигрышей 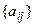
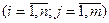 .
.
Такая ЗПР называется также «игрой с природой».
| состояния среды | ||||||

| 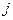
| 
| 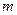
| |||
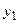
| 
| 
| 
| 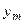
| ||
| Альтернативы | 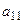
| 
| 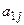
| 
| 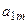
| |
| 
| 
| 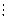
| |||
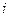
| 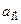
| 
| 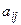
| 
| 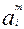
| |
| 
| 
| 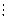
| |||
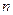
| 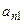
| 
| 
| 
| 
|
Выбирая 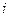 -ю альтернативу, получаем один из выигрышей
-ю альтернативу, получаем один из выигрышей  с вероятностью
с вероятностью 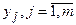 соответственно. Таким образом, исходом является величина
соответственно. Таким образом, исходом является величина 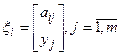 . Следовательно, сравнение альтернатив и сводится к сравнению соответствующих им случайных величин. Для этого используется математическая ожидание
. Следовательно, сравнение альтернатив и сводится к сравнению соответствующих им случайных величин. Для этого используется математическая ожидание 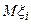 и дисперсия
и дисперсия 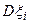 . Математическое ожидание показывает величину ожидаемого выигрыша, а дисперсия – величину риска. Часто используется не дисперсия, а среднеквадратичное отклонение (СКО):
. Математическое ожидание показывает величину ожидаемого выигрыша, а дисперсия – величину риска. Часто используется не дисперсия, а среднеквадратичное отклонение (СКО): 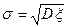 . Получаем двухкритериальную задачу.
. Получаем двухкритериальную задачу.
Чтобы получить представление о математическом ожидании, рассмотрим следующую ситуацию: группа сдает три экзамена.
| Среднее | |||||||
| Оценка | |||||||
| Отклонение | -1 | -1 | -1 | ||||
| СКО |
Результат: 4  1.
1.
Другой пример:
| Среднее | |||||||
| Оценка | |||||||
| Отклонение | -1 | -1 | |||||
| СКО |
Подход А. Использование обобщенного критерия: 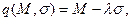 где
где  - некоторая постоянная, определяемая ЛПР. Этот критерий – взвешенная сумма М и
- некоторая постоянная, определяемая ЛПР. Этот критерий – взвешенная сумма М и  с весами 1 и (-
с весами 1 и (-  ). При
). При 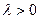
 , что характеризует ЛПР как человека, не склонного к риску. При
, что характеризует ЛПР как человека, не склонного к риску. При  , наоборот,
, наоборот, 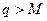 , что характеризует ЛПР как человека, склонного к рискую Если же
, что характеризует ЛПР как человека, склонного к рискую Если же 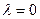 , то, следовательно, ЛПР безразличен к риску.
, то, следовательно, ЛПР безразличен к риску.
Таким образом,  – субъективный показатель меры склонности к риску (показатель осторожности). Будем считать, что ЛПР не склонен к риску (
– субъективный показатель меры склонности к риску (показатель осторожности). Будем считать, что ЛПР не склонен к риску ( 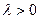 ). Тогда критерий М будет позитивным, а
). Тогда критерий М будет позитивным, а  – негативным. Возьмем из множества альтернатив
– негативным. Возьмем из множества альтернатив 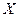 две альтернативы
две альтернативы  и
и 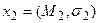 . Тогда
. Тогда  ,
, 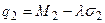 .
.
Возможны два случая:
а) Альтернативы 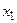 и
и 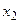 сравнимы по Парето.
сравнимы по Парето.
Пусть 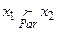 . Тогда
. Тогда 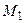
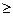
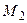 и
и 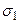
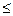
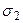 (причем хотя бы одно из этих неравенств является строгим)
(причем хотя бы одно из этих неравенств является строгим) 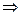
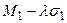 >
> 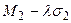 , то есть
, то есть  >
> 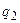 . Таким образом, в этом случае независимо от меры склонности ЛПР к риску (от значения
. Таким образом, в этом случае независимо от меры склонности ЛПР к риску (от значения 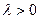 )
) 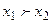 .
.
б) Альтернативы 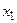 и
и 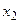 несравнимы по Парето.
несравнимы по Парето.
Пусть, пример, 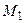 >
> 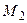 и
и 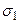 >
> 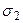 (больше ожидаемый выигрыш и больше риск). Тогда
(больше ожидаемый выигрыш и больше риск). Тогда 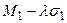 >
> 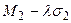
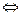
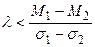 . Таким образом,
. Таким образом, 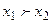 , если
, если 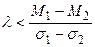 ;
; 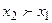 , если
, если  .
.
В многокритериальной ЗПР основная трудность – в выборе одной оптимальной альтернативы из множества Парето-оптимальных альтернатив. Она легко преодолевается, если Парето-оптимальные альтернативы проранжировать по предпочтению. Это можно сделать с использованием вышеприведенных формул.
Найдем 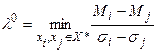 и
и 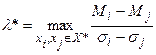 , где
, где 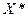 – множество Парето-оптимальных альтернатив (
– множество Парето-оптимальных альтернатив (  >
>  и
и 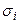 >
> 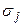 ).
).
Назовем 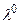 нижней границей несклонности к риску, а
нижней границей несклонности к риску, а 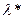 верхней границей несклонности к риску. Тогда всегда выполняется
верхней границей несклонности к риску. Тогда всегда выполняется 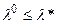 .
.
Правила:
1) Если у ЛПР  , то для этого ЛПР ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию должно совпадать с ранжированием по показателю ожидаемого выигрыша
, то для этого ЛПР ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию должно совпадать с ранжированием по показателю ожидаемого выигрыша  , то есть более предпочтительней будет альтернатива с большим
, то есть более предпочтительней будет альтернатива с большим  .
.
2). Если у ЛПР 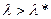 , то для этого ЛПР ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию должно совпадать с ранжированием по показателю риска
, то для этого ЛПР ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию должно совпадать с ранжированием по показателю риска  (есть более предпочтительной будет альтернатива с меньшим риском).
(есть более предпочтительной будет альтернатива с меньшим риском).
Показатель  (мера склонности к риску) предлагается определять на основе психологических качеств ЛПР на основе наблюдения за тем, как ЛПР принимает решения в различных ситуациях.
(мера склонности к риску) предлагается определять на основе психологических качеств ЛПР на основе наблюдения за тем, как ЛПР принимает решения в различных ситуациях.
Подход В. Использование отношений доминирования по Парето.
Пусть ЛПР не склонен к риску, тогда  будет позитивным критерием, а
будет позитивным критерием, а  –негативным.
–негативным.
 Условие доминирование по Парето
Условие доминирование по Парето  означает, что для альтернативы
означает, что для альтернативы 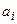 получается такой же (или больший) ожидаемый выигрыш, но с меньшим (или таким же) риском.
получается такой же (или больший) ожидаемый выигрыш, но с меньшим (или таким же) риском.
Окончательный выбор альтернативы производится из этого множества на основе неформальных добавочных соображений. При втором подходе производится сужение множества Парето с применением ранее изученных методов.
Пример: выбор варианта производимого товара.
Фирма может выпускать продукцию одного из следующих типов: зонты (З), куртки (К), плащи (П), сумки (С), шляпы (Ш), туфли (Т). Глава фирмы должен решить, какую продукцию выпускать предстоящим летом. Прибыль фирмы зависит от того, каким будет лето: дождливым (Д), жарким (Ж) или умеренным (У). Пусть ЛПР имеет информацию о вероятности наступления дождливого, жаркого или умеренного лета:
| Д (0,2) | Ж (0,5) | У (0,3) | |
| З | |||
| К | |||
| П | |||
| С | |||
| Т | |||
| Ш |
Ожидаемый выигрыш:
М(З)=80*0,2+60*0,5+40*0,3=58;
М(К)=58;
М(П)=57;
М(С)=56;
М(Т)=55;
М(Ш)=62,5.
Определим дисперсии (по формуле 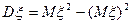 )
)
D  (З)=6400*0,2+3600*0,5+1600*0,3-(58)
(З)=6400*0,2+3600*0,5+1600*0,3-(58) 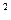 =196;
=196;
D  (К)=336;
(К)=336;
D  (П)=61;
(П)=61;
D  (С)=84;
(С)=84;
D  (Т)=100;
(Т)=100;
D  (Ш)=231,5.
(Ш)=231,5.
Среднеквадратичное отклонение:
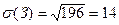 ;
;
 ;
;
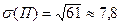 ;
;
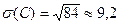 ;
;
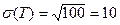 ;
;
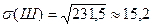 .
.
| М | 
| |
| З | ||
| К | 18,3 | |
| П | 7,8 | |
| С | 9,2 | |
| Т | ||
| Ш | 62,5 | 15,2 |
Результат сводим в таблицу:
Парето-оптимальное множество –  . Из него выбирается одна альтернатива.
. Из него выбирается одна альтернатива.
Найдем оптимальное решение с помощью обобщенного критерия: q(З)=58-14  ; q(С)=56-9,2
; q(С)=56-9,2  ; q(К)=58-18,3
; q(К)=58-18,3  ; q(Т)=55-10
; q(Т)=55-10  ; q(П)=57-7,8
; q(П)=57-7,8  ; q(Ш)=62,5-15,2
; q(Ш)=62,5-15,2  .
.
Найдем 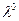 и
и 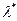 :
:
 =
= 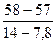 =0,16;
=0,16;  =
= 
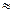 3,8;
3,8; 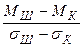 =
= 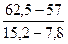 =0,74.
=0,74.
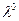 =min(0,16; 3,8; 0,74)=0,16;
=min(0,16; 3,8; 0,74)=0,16; 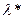 =max(0,16; 3,8; 0,74)=3,8.
=max(0,16; 3,8; 0,74)=3,8.

По правилу ранжирования получаем:
1) Если для ЛПР 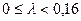 , то Ш
, то Ш  З
З  П. Оптимальная альтернатива – Ш.
П. Оптимальная альтернатива – Ш.
2) Если для ЛПР  , то П
, то П  З
З  Ш. Оптимальная альтернатива – П.
Ш. Оптимальная альтернатива – П.
3) Если для ЛПР 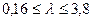 , например,
, например, 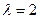 . Тогда:
. Тогда:
q(З)=58-14*2=30; q(П)=57-7,8*2=41,4; q(Ш)=62,5-15,2*2=32,1. Получаем П 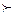 Ш
Ш 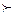 З.
З.
14. Оценка многокритериальных альтернатив – подход аналитической иерархии
Автор: Т. Саати. Analytic Hierarchy Process (AHP).
Данный подход широко известен в настоящее время. Типичная постановка задачи, решаемой этим методом, заключается обычно в следующем: дана общая цель решения задачи, 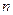 альтернатив и
альтернатив и 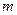 критериев оценки альтернатив. Требуется выбрать наилучшую альтернативу.
критериев оценки альтернатив. Требуется выбрать наилучшую альтернативу.
Подход AHP состоит из ряда этапов:
1) Структуризация задачи в виде иерархической структуры с несколькими уровнями: цели – критерии – альтернативы.
2) ЛПР выполняет попарное сравнение элементов каждого уровня. Результаты сравнений переводятся в числа с помощью специальной таблицы.
3) Вычисляются коэффициенты важности для элементов каждого уровня, при этом проверяется согласованность суждений ЛПР.
4) Подсчитывается количественный индикатор качества каждой из альтернатив и определяется лучший из них.
В качестве примера рассмотрим ситуацию выбора места для постройки аэропорта. Критерии для оценки альтернатив таковы: C1 – стоимость постройки (желательно подешевле), C2 – расстояние до города (желательно, чтобы расстояние было меньше), C3 – минимальное шумовое воздействие (число людей, подвергающихся шуму, должно быть минимально). Эти критерии противоречивы. Например: постройка аэропорта вдали от города возможно потребует меньших затрат, но время поездки будет больше.
Структуризация.
Предположим, что предварительно выбрали четыре варианта (A,B,C,D). Тогда структура решаемой задачи будет выглядеть так:
A (180, 70, 10)
B (170, 40, 15)
C (160, 55, 20)
D (150, 50, 25)
Дата добавления: 2016-03-20; просмотров: 646;
