Принятие решений в условиях неопределенности
Оно характеризуется тем, что при выборе альтернативы ЛПР не знает состояние среды и не имеет информации о вероятностях их проявления. Однако ЛПР известно множество возможных состояний среды и функция реализации 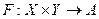 , где
, где 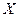 – множество допустимых альтернатив,
– множество допустимых альтернатив, 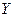 – множество состояний среды,
– множество состояний среды, 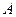 – множество исходов.
– множество исходов.
Оценочная структура представлена функцией 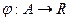 . Тогда целевая функция
. Тогда целевая функция 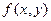 указывает полезность (ценность) того исхода, который получается в результате, когда ЛПР выбирает альтернативу
указывает полезность (ценность) того исхода, который получается в результате, когда ЛПР выбирает альтернативу 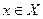 , а среда находится в состоянии
, а среда находится в состоянии 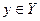 . Таким образом,
. Таким образом, 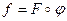 .
.
Пример: аренда комнат в отеле, 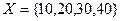 – число комнат,
– число комнат, 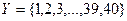 – степень заполнения комнат
– степень заполнения комнат
В ячейках следующей таблицы должна содержаться соответствующая прибыль:

| ||||||

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
|
Здесь 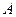 – прибыль от аренды. Если
– прибыль от аренды. Если 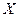 и
и 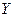 конечны, то целевая функция может быть задана таблично. Если приписать элементам множеств
конечны, то целевая функция может быть задана таблично. Если приписать элементам множеств 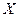 и
и 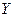 номера, то
номера, то 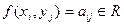 – выигрыш ЛПР в случае выбора
– выигрыш ЛПР в случае выбора 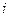 -го варианта при
-го варианта при 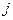 -ом состоянии среды.
-ом состоянии среды.
Пусть 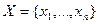 ,
, 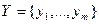 . Тогда матрица выигрышей (платежная матрица) имеет вид
. Тогда матрица выигрышей (платежная матрица) имеет вид
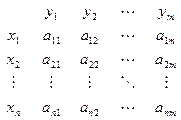
Подходы к сравнению альтернатив, представленных в платежной матрице.
1-й подход. Использование принципа доминирования. Он заключается в отбрасывании доминируемых альтернатив. Тогда 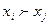 , если
, если 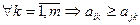 , в противном случае
, в противном случае  и
и 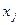 несравнимы по доминированию. Пример:
несравнимы по доминированию. Пример:
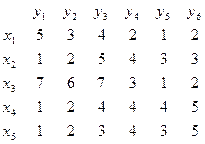
При попарном сравнении 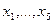 имеем:
имеем: 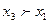 ,
, 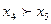 , причем других пар, находящихся в отношении доминирования, нет, то есть альтернативы
, причем других пар, находящихся в отношении доминирования, нет, то есть альтернативы 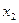 ,
, 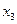 и
и 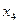 несравнимы по отношению доминирования. Для выбора оптимальной альтернативы из оставшихся необходимо использование других методов.
несравнимы по отношению доминирования. Для выбора оптимальной альтернативы из оставшихся необходимо использование других методов.
2-й подход. Основной принцип: формулируется некоторая гипотеза о поведении среды, позволяющая дать каждой альтернативе единую числовую оценку, которая даёт критерии для сравнения альтернатив по предпочтению. Оптимальной будет альтернатива, имеющая наибольшую оценку (для функции потерь – наименьшую).
Основные типы критериев:
1) Критерий Лапласа. Критерий основан на гипотезе равновероятности (равновозможности) состояний среды. Тогда оценка 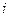 -й альтернативы равна
-й альтернативы равна 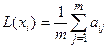 и
и 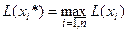 . Недостаток такого подхода состоит в эффекте компенсации маленьких выигрышей большими.
. Недостаток такого подхода состоит в эффекте компенсации маленьких выигрышей большими.
2) Критерий Вальда. Критерий основан на гипотезе антагонизма, то есть при выборе решения надо рассчитывать на самый худший возможный вариант. Тогда оценкой 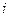 -й альтернативы служит число
-й альтернативы служит число 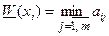 и
и 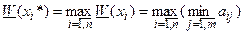 .
. 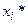 – максиминная альтернатива. Принцип максимина - максимизация минимально возможного (то есть гарантированного) выигрыша. Еще одно название – принцип максимального гарантированного результата. Недостаток: при выборе решения учитывается только наихудший вариант.
– максиминная альтернатива. Принцип максимина - максимизация минимально возможного (то есть гарантированного) выигрыша. Еще одно название – принцип максимального гарантированного результата. Недостаток: при выборе решения учитывается только наихудший вариант.
Если целевая функция является функцией потерь, то оценкой альтернативы 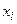 является число
является число 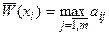 и
и 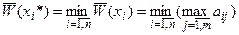 . Тогда
. Тогда 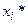 – минимаксная альтернатива (минимакс). Это – принцип минимизации максимально возможных потерь.
– минимаксная альтернатива (минимакс). Это – принцип минимизации максимально возможных потерь.
3) Критерий Гурвица. Критерий связан с введением показателя 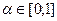 , называемого показателем пессимизма.
, называемого показателем пессимизма.  Гипотеза поведения среды: вероятность наихудшего состояния равна
Гипотеза поведения среды: вероятность наихудшего состояния равна  , а наилучшего –
, а наилучшего – 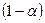 . Тогда оценка альтернативы
. Тогда оценка альтернативы 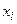 :
: 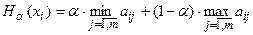 . Если
. Если 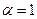 , то это критерий крайнего пессимизма (критерий Вальда). Если
, то это критерий крайнего пессимизма (критерий Вальда). Если 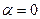 , то это критерий крайнего оптимизма. Недостаток: учитываются только два крайних исхода; субъективность определения показателя
, то это критерий крайнего оптимизма. Недостаток: учитываются только два крайних исхода; субъективность определения показателя  .
.
4) Критерий Сэведжа. Критерий основан на преобразовании первоначальной матрицы выигрышей 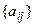 в матрицу рисков (матрицу сожалений)
в матрицу рисков (матрицу сожалений) 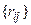 . Риском при выборе альтернативы
. Риском при выборе альтернативы 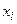 в состоянии
в состоянии  называется число
называется число 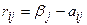 , где
, где 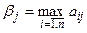 . Оптимальная альтернатива минимизирует максимальный риск, то есть используется минимаксный критерий для матрицы сожалений.
. Оптимальная альтернатива минимизирует максимальный риск, то есть используется минимаксный критерий для матрицы сожалений.
Оптимальные решения, получаемые по указанным критериям, в общем случае могут не совпадать, так как критерии противоречат друг другу, поскольку основаны на разных гипотезах.
Пример: необходимо выбрать проект электростанции. Возможно 4 варианта: 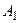 – ТЭЦ,
– ТЭЦ, 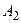 – ГЭС,
– ГЭС, 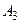 – АЭС,
– АЭС, 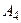 – ПЭС. Состояния среды, влияющие на строительство и дальнейшую эксплуатацию, учитывает следующие факторы: погода, возможность наводнения, цена топлива, расходы на его транспортировку. Пусть выделено 4 варианта комбинаций факторов:
– ПЭС. Состояния среды, влияющие на строительство и дальнейшую эксплуатацию, учитывает следующие факторы: погода, возможность наводнения, цена топлива, расходы на его транспортировку. Пусть выделено 4 варианта комбинаций факторов: 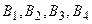 . В матрице выигрышей показана эффективность каждого из вариантов:
. В матрице выигрышей показана эффективность каждого из вариантов:
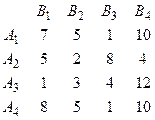
1) Критерий Лапласа. Здесь 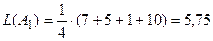 ;
; 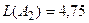 ;
; 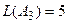 ;
; 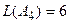 . Таким образом,
. Таким образом, 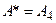 – оптимальная альтернатива.
– оптимальная альтернатива.
2) Критерий Вальда. 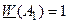 ;
; 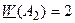 ;
; 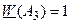 ;
; 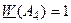 . Таким образом,
. Таким образом, 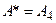 – оптимальная альтернатива.
– оптимальная альтернатива.
3) Критерий Гурвица. Пусть 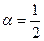 ; тогда
; тогда 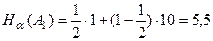 ;
; 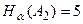 ;
; 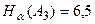 ;
;  . Таким образом,
. Таким образом, 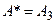 – оптимальная альтернатива.
– оптимальная альтернатива.
Оценим влияние  на результат. В данной задаче
на результат. В данной задаче 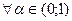
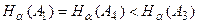 , поэтому остается две альтернативы, которые могут стать оптимальными:
, поэтому остается две альтернативы, которые могут стать оптимальными: 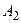 и
и 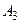 . Условие
. Условие 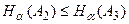 сводится к неравенству
сводится к неравенству 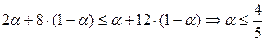 . Таким образом, при
. Таким образом, при 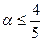 оптимальной будет альтернатива
оптимальной будет альтернатива 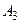 , а при
, а при 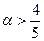 оптимальной будет
оптимальной будет 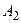 .
.
4) Критерий Сэведжа. Преобразуем матрицу выигрышей в матрицу рисков.
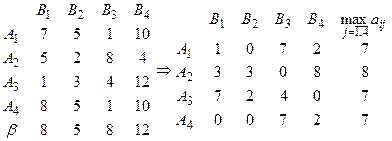
Таким образом, 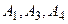 – оптимальные альтернативы.
– оптимальные альтернативы.
Дата добавления: 2016-03-20; просмотров: 1070;
