Основные типы моделей

Из различных модификаций линейных возрастающих случайных функций изменения ОП Х(t) или ln X(t) наиболее часто процесс приближения объекта к отказам аппроксимируется следующими типами моделей:

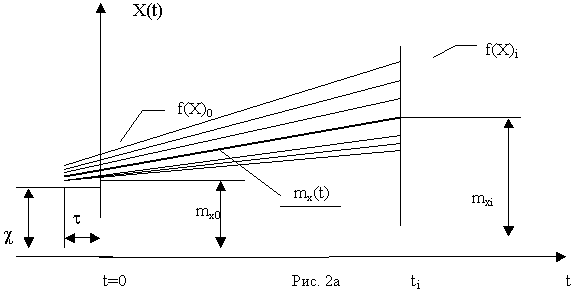
а) веерной с ненулевым начальным рассеиванием (рис. 2a);

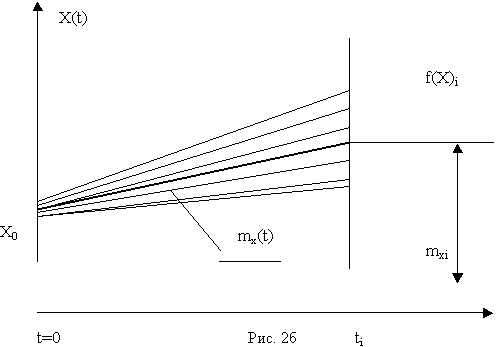
б) веерной с нулевым начальным рассеиванием (рис. 2б);

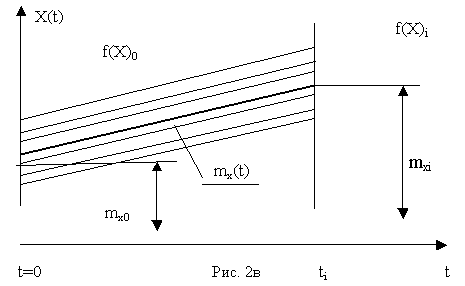
в) равномерной (рис. 2в).

Тип модели линейной функции Х(t) или ln X(t) зависит от числа случайных аргументов, определяющих ее случайный характер.

Веерная функция с ненулевым начальным рассеиванием описывается:

- для процесса X(t)

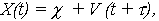
(10)

- для процесса ln X(t)

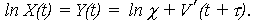
(11)

При t = 0 значения функций (12) и (13) представляют собой случайную величину, соответственно

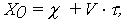
(12)

и

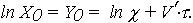
(13)

причем V = V' . С учетом (12) и (13) модели (10), (11) легко представляются в виде (5) и (9). Случайный характер рассмотренной модели определяется двумя случайными аргументами: X₀ или ln X₀ - случайное начальное значение ОП или его логарифма; V или V' - случайная скорость изменения ОП или его логарифма.

Как следует из рис. 2a, все реализации веерной линейной случайной функции с ненулевым начальным рассеиванием проходят через общую неслучайную точку - "полюс".

Аргумент рассмотренной модели - случайная скорость изменения ОП (V) или логарифма ОП (V ) - имеет нормальное распределение с плотностью распределения соответственно:

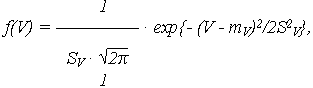
(14)

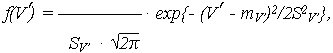
(15)

Линейно зависящая от V случайная функция Х(t) (10) во всех 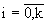сечениях будет распределена нормально с плотностью

и параметрами распределения:

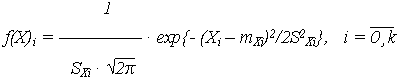
(16)

- матожидание m_Xi = M{X_i};

- среднее квадратичное отклонение

- Численные характеристики - матожидание mx(t) и СКО Sx(t), самой случайной функции (10) выражаются через числовые характеристики m_v и S_v случайной скорости:

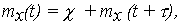
(17)

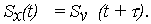
(18)

Cлучайное начальное значение ОП X₀ соответствует сечению функции Х(t) (10) при t =0, поэтому также имеет нормальное распределение по (16) при i = 0 с параметрами m_x(t = 0) = m_x0 и СКО S_x(t = 0) = S_x0 , определяемыми из (17) и (18) при t=0:

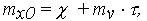
(19)

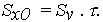
(20)

С учетом (19) и (20) выражения (17), (18) для числовых характеристик случайной функции (10) изменения ОП Х(t) примут вид:

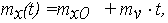
(21)

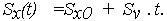
(22)

В соответствие с (11) нормальное распределение скорости V' приводит к тому, что линейно зависящий от V' логарифм ОП ln X(t) = Y(t) также будет распределен нормально во всех 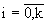- сечениях с плотностью распределения

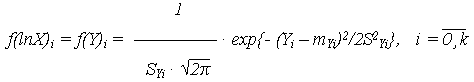
(23)

Cам же ОП при этом будет иметь логарифмически нормальное распределение, плотность которого:

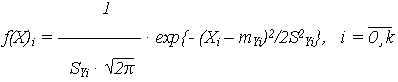
(24)

В выражениях (23), (24)

m_yi = M{lnX_i},

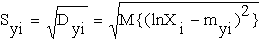- соответственно, матожидание и СКО логарифма ОП в 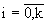сечениях случайной функции (11).

Матожидание m_y(t) и СКО S_y(t) линеаризованной путем логарифмирования функции (11) можно получить, используя числовые характеристики случайной скорости V : m_v' и S_v'. Проводя аналогичные, как для функции (10), преобразования, получаем числовые характеристики модели (11) изменения логарифма ОП lnX(t) = Y(t):

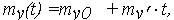
(25)

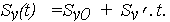
(26)

Веерная функция с нулевым начальным рассеиванием является частным случаем модели (5), (9) и может быть получена из указанных выражений путем замены в них, соответственно, случайных начальных значений ОП Х₀ или его логарифма lnX₀ = Y₀ некоторым неслучайным значением K₀ или lnK₀.

Поскольку веерная модель с ненулевым начальным рассеиванием является

частным случаем моделей (10), (11), то ее свойства определяются свойствами указанных моделей, поэтому числовые характеристики определяются (без вывода):

- для функции Х(t) = K₀ + Vt изменения ОП из (21), (22)

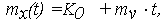
(27)

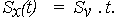
(28)

- для функции Y(t) = lnX(t) = lnK₀ + V't изменения ОП из (25), (26)

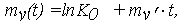
(29)

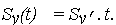
(30)

Равномерная функция также является частным случаем моделей (5), (9) и может быть получена из последних путем замены в них соответственно случайных скоростей изменения ОП V или его логарифма V' на неслучайные (постоянные) скорости 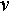или '.

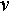Числовые характеристики случайных функций определяются (без вывода):

- для функции изменения ОП Х(t) = X₀ + 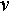t из (21), (22)

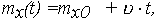
(31)

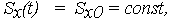
(32)

- для функции Y(t) = lnX(t) = Y0 + 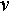't из (25), (26)

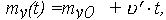
(33)

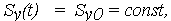
(34)

Рассмотренные линейные модели удобны для аппроксимации случайных процессов изменения ОП тем, что позволяют характеризовать эти процессы ограниченным числом аргументов модели, для определения которых требуется минимальный объем экспериментальных данных.