ДО ТЕМИ 3 АНАЛІЗ ТА ОЦІНКА ФІНАНСОВИХ ІНВЕСТИЦІЙ – 1 практика
При розробці оптимальних фінансових рішень в конкретних ситуаціях інвестор має вміти оцінювати майбутню вартість інвестованих грошових коштів.
Оцінка майбутньої вартості грошових вкладень, інвестованих на строк більше одного року (періоду) залежить від того який процент (простий чи складний) буде прийматися в розрахунках. При використанні простого відсотку інвестор буде одержувати доход (нарощувати капітал) тільки з суми початкових інвестицій протягом всього строку реалізації проекту. При використанні складного проценту, одержаний доход періодично додається до суми початкових інвестицій. У результаті чого відсоток нараховується також з накопиченої у попередніх періодах суми відсоткових платежів або будь-якого іншого виду доходу. Знаходження майбутньої вартості грошових коштів через п - період і при відомому значенні темпу їх приросту здійснюється за такою формулою:
FVn = PV ( 1 + r)n = PV· FVIF r, n, (3.3)
де PV – сума грошових коштів, інвестованих у період t=0;
r – ставка відсотку, коефіцієнт;
n – кількість періодів (років)$
FVIF r, n – фактор майбутньої вартості грошових вкладень, коефіцієнт.
Приклад 1. Інвестор поклав у банк 500 грн. під 10% річних. Визначити величину суми вкладу через 4 роки.
FV4 = 500 (1 + 0,1) 4 = 500 х 1,4641 = 732,05 грн.
Якщо нарахування відсотків здійснюється m – раз у рік, то формула буде мати такий вигляд:
FVn = PV ( 1 + r/ m)n·m (3.4)
Приклад 2.Інвестор поклав у банк 500грн. під 10% річних з щоквартальним нарахуванням відсотків. Визначити величину суми вкладу через 3 роки.
FV3, 4 = 500 (1 + 0,1/ 4) 3·4 = 672,44 грн.
Процес, в якому при заданих значення PV та r необхідно знайти величину майбутньої вартості інвестованих коштів до кінця певного періоду часу (n) називається операцією нарощування.
У фінансових розрахунках часто виникає потреба в оцінці поточної вартості майбутніх грошових потоків (PV). Метою даної процедури є визначення цінностей майбутніх надходжень від реалізації того чи іншого проекту з позицій поточного моменту. Процес конвертування грошових коштів, що планується одержати у майбутніх періодах в їх поточну вартість називається операцією дисконтування. Процентна ставка, що використовується у розрахунку PV називається дисконтною ставкою. А показник поточної вартості визначається за такою формулою:
PV = FVn ·1/( 1 + r)n,(3.5)
де 1/( 1 + r)n - називається фактором (множником) поточної вартості (PVFVr, n ).
Приклад 3. Визначити, яку суму необхідно положити на депозит, щоб через 3 роки власник депозиту одержав 4 тис. грн., якщо ставка відсотку становить 12% річних.
PV = 4000 ·1/( 1 + 0,12)3 = 2850 грн.
Якщо нарахування відсотків планується здійснювати більше одного разу у період, то формула буде мати такий вигляд:
PV = FVn ·1/( 1 + r/ m)n m (3.6)
Крім номінальної ставки відсотку за депозит r, у фінансових розрахунках використовується і ефективна ставка, або дійсна ставка відсотку. Ця ставка визначає той відносний доход, який одержує власник капіталу за рік у цілому. Іншими словами, це річна ставка доходності, яку одержує інвестор при m - раз нарахувань у році за ставкою відсотку r/ m. Таким чином, ефективна ставка складних відсотків визначається за формулою:
EAR = (1+r/m) m – 1 = FVIF r/m, m – 1 (3.7)
Приклад 4. Є два варіанти нарахування відсотків на кошти, які розміщуються на депозит у банк. За варіантом А – нарахування здійснюється щомісячно за ставкою 24% річних, а за варіантом В – щоквартально за ставкою 28% річних. Визначити ефективну річну ставку за кожним варіантом.
Варіант А: EAR = (1 + 0,24/12)12 – 1 =1,268 - 1 = 0, 268 (26,8%)
Варіант В: EAR = (1 + 0,28/4)4 – 1 =1,3108 - 1 = 0, 3108 (31,08%)
Таким чином, варіант В є привабливішим ефективна ставка відсотку більша.
У інвестиційному аналізі виникає необхідність оцінити грошові потоки, якігенеруються інвестиційним проектом у різні періоди часу. Одним з способів оцінки їх є представлення цих потоків у вигляді аннуітету, або фінансової ренти, який представляє собою рівні за величиною грошові потоки за кожний період протягом точно визначеного часу.
Узагальнюючими показниками ренти є нарощена (майбутня) сума ренти та сучасна (поточна, приведена) рента.
Нарощена сума – це сума усіх членів потоку платежів з нарахуванням на них відсотків в кінці строку , тобто на дату останньої виплати. Цей показник показує яку величину буде представляти капітал, який вноситься через рівні проміжки часу протягом усього строку ренти з нарахованими відсотками.
Майбутня вартість звичайного аннуітету (FVA n) протягом періоду n визначається за формулою:
FVA n = P ·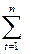 
FVIFr, n-1 = P · FVIFA r, n , (3.8)
де P – періодичні надходження рівні за величиною грошові потоки;
FVIFA r, n – фактор майбутньої вартості аннуітету, коефіцієнт.
Показник, який характеризує майбутню вартість однієї грошової одиниці в кінці строку реалізації інвестиційного проекту (коефіцієнт нарощування ренти або коефіцієнт накопичення грошової одиниці за період) визначається за формулою:
FVIFA r, n = 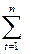(1 + r)n-t = [(1+r)n – 1) / r](3.9)
Приклад 5. Приміщення здається в оренду на 5 років. Орендні платежі вносяться у розмірі 10 тис. грн. орендатором щорічно в кінці року в банк на рахунок власника компанії. Банк нараховує на ці суми 20% річних. Визначити суму, яку одержить власник компанії в кінці строку оренди, при умові, якщо гроші з рахунку не знімалися.
FVA 5 = 10 · [(1+0,2) 5 – 1) / 0,2] = 74,416 тис. грн.
Сучасна величина ренти ( поточна вартість аннуітету)– це сума усіх членів ренти, дисконтованих на момент приведення по вибраній дисконтній ставці.
PVA n = P · 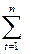PVIFr, n-1 = P · PVIFA r, n , (3.10)
де PVAn – поточна вартість звичайного аннуітету з строком інвестування n періодів;
PVIFA r, n – фактор поточної вартості аннуітету, коефіцієнт, який визначається за формулою:
PVIFA r, n = 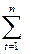(1 + r) -n = [(1-(1+r)-n) / r](3.11)
Приклад 6. Фірма передбачає створити протягом 3-х років фонду інвестування у розмірі 150 тис. грн. Фірма має можливість асигнувати на це щорічно 41,2 тис. грн., розміщуючи їх під 20% річних. Яка сума потрібна фірмі для створення фонду у розмірі 150 тис. грн. , якщо вона помістила б її у банк одночасно на 3 роки під 20% річних?
PVA 3 = 41,2 ·[(1-(1+0,2)-3) / 0,2] = 86,79 тис. грн.
Дійсно, якщо б фірма положила цю суму у банк на 3 роки під 20% річних то одержала б:
86,79 · (1+0,2)3 = 149,973 тис. грн. ( ≈ 150 тис. грн. )
В той же час нарощена сума при щорічних платежах у розмірі 41,2 тис. грн. під 20% становитиме:
FVA 3 = 41,2 · [(1+0,2) 3 – 1) / 0,2] = 149,968 тис. грн. ( ≈ 150 тис. грн.)
Дата добавления: 2016-03-20; просмотров: 602;