Занятие 7. Термодинамика

Задача 04.1.1.1

Вычислитьγпоказатель адиабатыдля газовой смеси, состоящей из ν₁ = 2,0 моля кислорода и

ν₂ = 3,0 моляуглекислого газа. Газы считать идеальными.

Дано: показатели адиабат для O₂ кислорода γ₁ =1, 40 и CO₂ углекислого газа γ₂ = 1, 30, количество молей O₂ кислорода ν₁ = 2,0 и CO₂ углекислого газа ν₂ = 3,0.Определить γпоказательадиабаты смеси.Молярная C_pтеплоемкость при постоянном давлениис учетом (4.57) из раздела 04.1.0 "Физическая термодинамика" имеет следующий вид: C_p = (i + 2)R/2, (1.1) где i - количество степеней свободы из параграфа "Закон равномерного распределения энергии по степеням свободы молекул" раздела 04.1.0 "Физическая термодинамика", котороедля двухатомноймолекулы O₂ кислорода i = 5, для трёхатомноймолекулы CO₂ углекислого газа i = 6; R = 8_,314 Дж/(моль∙K) - универсальная газовая постоянная.

Показательγ (4.67)из раздела 04.1.0 "Физическая термодинамика" адиабаты имеет следующий вид: γ = C_p/C_V, (1.2) где C_V - молярная (4.52) из раздела 04.1.0 "Физическая термодинамика" теплоемкость при V постоянном объеме.

Подставляем (1.1) в (1.2) и решаем полученное выражение относительно молярной C_V теплоемкости при V постоянном объеме, после чего получаем следующее выражение: C_V = (i + 2)R/2γ, (1.3) Молярная (4.52) из раздела 04.1.0 "Физическая термодинамика" C_Vтеплоемкость при V постоянном объеме имеет следующий вид: C_V = iR/2 ↔ i = 2C_V/R. (1.4) Подставляем (1.4) в (1.3) и решаем полученное выражение относительно молярной C_V теплоемкости при V постоянном объеме, после чего получаем следующее выражение:

C_V = R/(γ -1). (1.5) C использованием (1.5) молярные C_V1, C_V2 теплоемкости при V постоянном объеме соответственно O₂ кислорода, CO₂ углекислого газа с учётом их γ₁, γ₂ показателей адиабат имеют следующий вид: C_V1 = R/(γ₁ -1); C_V2 = R/(γ₂-1). (1.6) ВнутренняяU (4.51) из раздела 04.1.0"Физическая термодинамика" энергия смеси O₂ кислорода ν₁ = 2,0 моля количеством с CO₂ углекислым газом ν₂ = 3,0 моля количеством имеет следующий вид: U = (ν₁ + ν₂)C_VT. (1.7) где C_V - молярная (4.52) из раздела 04.1.0 "Физическая термодинамика" теплоемкость смеси O₂ кислорода с CO₂ углекислым газом при V постоянном объеме при T температуре этой газовой смеси.

Подставляем в (1.7) выражение (1.5) молярной C_V теплоемкости при V постоянном объеме, где

γ- показатель адиабатысмеси O₂ кислорода и CO₂ углекислого газа, и получаем следующее выражение

Uвнутреннейэнергии этой смеси: U = (ν₁ + ν₂)RT/(γ -1). (1.8) ВнутренняяU (4.51) из раздела 04.1.0"Физическая термодинамика" энергия смеси, выраженная через U₁ и U₂ внутренниеэнергии O₂ кислорода ν₁ = 2,0 моля количеством с CO₂ углекислым газом ν₂ = 3,0 моля количеством имеет следующий вид: U = U₁ + U₂ ↔ U = ν₁ C_V1T + ν₂ C_V2T. (1.9) Подставляем в (1.9) молярные C_V1, C_V2 теплоемкости при V постоянном объеме из (1.6) соответственно O₂ кислорода и CO₂ углекислого газа с учётом их показателейγ₁, γ₂ адиабат и получаем следующее выражение Uвнутреннейэнергии смеси этих O₂ кислорода и CO₂ углекислого газа: U = [ν₁ R/(γ₁ -1)T] +[ ν₂ R/(γ₂ -1)T]. (1.10) Выражения (1.8) и (1.10) определяют Uвнутреннюю энергию смеси O₂ кислорода ν₁ = 2,0 моля количеством с CO₂ углекислым газом ν₂ = 3,0 моля количеством. При этом в (1.8) выражении U внутренняя энергия включает в себя параметры смеси, т.е. γ- показатель адиабатысмеси и её общее

ν = (ν₁ + ν₂) количество молей, а в (1.10) выражении U внутренняя энергия включает в себя параметры компонентэтой смеси, т.е.γ₁, γ₂ показатели адиабат и ν₁, ν₂ количество молей соответственно O₂ кислорода и CO₂ углекислого газа. Поэтому эти два выражения (1.8) и (1.10) описывают один и тот же параметр, а именно Uвнутреннюю энергию смеси O₂ кислорода ν₁ = 2,0 моля количеством с CO₂ углекислым газом ν₂ = 3,0 моля количеством. Приравниваем выражения (1.8), (1.10) и решаем полученное выражение относительно требуемого в задаче γпоказателя адиабатысмеси O₂ кислорода и CO₂ углекислого газа, после чего получаем следующее выражение: (ν₁ + ν₂)RT/(γ -1) =

= [ν₁ R/(γ₁ -1)T] +[ ν₂ R/(γ₂ -1)T] ↔ γ = [ν₁ γ₁ (γ₂ -1) + ν₂ γ₂ (γ₁ -1)] /[ν₁ (γ₂ -1) + ν₂ (γ₁ -1)].(1.11) Задача 04.1.1.2

Один моль кислорода, находившегося при T₁ = 290 K температуре, адиабатическисжали так, что его давление возросло в η = 10 раз. Найти: а) температуру T₂ газа после сжатия; б) работу A′, которая была совершена над газом.

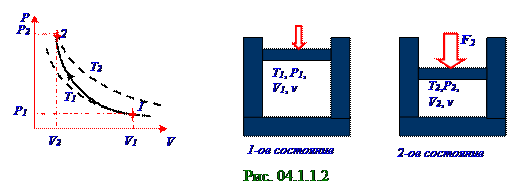
РаботаA₁₂′ (рис. 04.1.1.2)вектора F внешнейсилы, которая равняется по модулю и противоположнапо знаку A₁₂ работегаза в адиабатическом процессе(4.103)из раздела 04.1.0 "Физическая термодинамика" по сжатиюO₂ кислорода ν = 1,0 моль количеством из 1-ого состояния с V₁ объёмом во 2-ое состояние с V₂ объёмом, в результате чего температураэтогогаза возрастаетот значения T₁ до значения T₂, имеет следующий вид: A₁₂′ = C_V ν(T₂ - T₁). (2.1)

Подставляем в (2.1) выражение (1.5) из"Задача 04.1.1" молярной C_V теплоемкости при постоянном V объеме O₂ кислорода с учётом его γпоказателя адиабаты и получаем работуA₁₂′

(рис. 04.1.1.2)вектора F внешнейсилы по сжатиюO₂ кислорода ν = 1,0 моль количеством из 1-ого состояния с V₁ объёмом во 2-ое состояние с V₂ объёмом, в результате чего температураэтогогаза возрастаетот значения T₁ до значения T₂, которая имеет следующий вид: A₁₂′ = νR(T₂ - T₁)/(γ -1). (2.2) Уравнение Пуассона(4.71) из раздела 04.1.0 "Физическая термодинамика" в параметрах

P давления и T температуры для 1-ого состояния и 2-ого состояния с учётом условия задачи имеет следующий вид: P₁T₁^γ/(1-γ) = P₂T₂^γ/(1-γ) ↔ P₁T₁^γ/(1-γ) = ηP₁T₂^γ/(1-γ) ↔ T₂ = T₁η^{( γ-1)/γ}. (2.3) Подставляем (2.3) в (2.1) и получаем A₁₂′ работу(рис. 04.1.1.2)вектора F внешнейсилы по сжатиюO₂ кислорода ν = 1,0 моль количеством от начальнойT₁ температуры с увеличением первоначальногоP₁ давления в η раз, которая имеет следующий вид: A₁₂′ = νRT₁[η^{( γ-1)/γ} - 1]/(γ -1) , Дж. (2.4) Задача 04.1.1.3

Имеется идеальный газ с γпоказателем адиабаты. Его C молярная теплоёмкость при некотором процессе зависит от T температурыэтого идеального газа в соответствии со следующим выражением: C = α/T, где α, Дж - известный размерный коэффициент. Найти: а) работу A₁₂, совершённую одним молем идеального газа при его нагреве от T₁ температуры до T₂ температуры, в η раз большей;

б) уравнение процесса в параметрах P давленияи V объёма.

Дано: C = α/T; T₂ = ηT₁; γ / A₁₂ = ? P(V) = ?

а) Первое начало термодинамики (4.7) из раздела 04.1.0 "Физическая термодинамика" в дифференциальномвиде имеет следующий вид: δQ = dU + δA. (3.1)

С учётом (4.46) из раздела 04.1.0"Физическая термодинамика" элементарного количества δQ теплоты, сообщаемого одному молю идеального газа, бесконечноdUмалогоизменения внутреннейэнергии(4.49) из раздела 04.1.0 "Физическая термодинамика"этого одного моля идеального газа а также с учётом δAэлементарнойработы (4.12) из раздела 04.1.0"Физическая термодинамика", выполненной идеальным газом, выражение (3.1) принимает следующий вид: CdT = C_VdT + pdV, (3.2)

Работа A₁₂, совершённая одним молем идеального газа при его нагреве от T₁ температуры до T₂ температуры, в η раз большей, определится интегрированием (3.3) в пределах от значения T₁ до значения T₂ = ηT₁ температуры: V₂ ηT₁ ηT₁

A₁₂ =∫ pdV = ∫αdT/T - ∫RdT/(γ -1)= (αlnη) - [RT₁(η -1)/(γ -1)]. (3.4) V₁ T₁ T₁

где V₁, V₂ - начальный и конечный объёмы идеального газа при его нагреве от T₁ температуры до

T₂ температуры, в η раз большей.

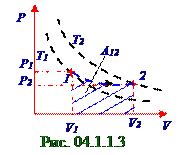
Графически (рис. 04.1.1.3) работа A₁₂, совершённая идеальным газом, представляет собой площадь под ориентировочной кривой зависимости P давленияот V объёма идеального газа, представленной на рис. 04.1.1.3 штриховой синей линией,при его нагреве от T₁ температуры до T₂ температуры, в η раз большей, что соответствует изменению объёма этого идеального газа от V₁ начальногодо V₂ конечного объёма.

Штриховой чёрной линией на рис. 04.1.1.3 изображены две изотермы, которые соединяют те точки на плоскости P давленияи V объёма идеального газа, при значении которых этот идеальный газ имеет постоянную T температуру. В частности в 1-ом состоянии, которому соответствуют P₁ давлениеи V₁ объём идеального газа, этот идеальный газ имеет T₁ температуру, поэтому нижняя изотермапроходит через 1 точку на плоскости P давленияи V объёма идеального газа. Во 2-ом состоянии, которому соответствуют P₂ давлениеи V₂ объём идеального газа, этот идеальный газ имеет

T₂ температуру, поэтому верхняя изотермапроходит через 2-ую точку на плоскости P давленияи

V объёма идеального газа.

б) Преобразовываем (3.3) в вид, удобныйдля интегрирования, после чего получаем следующее выражение для одного моляидеального газа: pdV - (αdT/T) + RdT/(γ -1)= 0. (3.5)

Подставляем в (3.5) P давлениес использованием (4.13) из раздела 04.1.0 "Физическая термодинамика" уравнения Клапейрона –Менделеевадля одного моляидеального газа: P = RT/V, после чего получаем следующее выражение:

(RTdV/V) - (αdT/T₀ )+ [RdT/(γ -1)] = 0 ↔ (dV/V) + [1/(γ -1)]dT/T = (α/R)(dT/T²). (3.6)

Производим интегрирование (3.6) от начального V₀ доконечногопеременного Vобъёма идеального газа, которым соответствует начальная T₀ и конечнаяпеременная T температура этого идеального газа, после чего получаем следующее выражение: V T T

∫ dV/V + [1/(γ -1)]∫dT/T = (α/R)∫dT/T² ↔ V₀ T₀ T₀

↔ lnV/V₀ + [1/(γ -1)]lnT/T₀ = (α/R)[(1/T) - (1/T₀ )]. (3.7)

Подставляем в (3.7) T температуру с использованием (4.13) из раздела 04.1.0 "Физическая термодинамика" уравнения Клапейрона –Менделеевадля одного моляидеального газа:

T = PV/R, T₀ = P₀V₀/R,после чего получаем следующее выражение:

lnV/V₀ + [1/(γ -1)]ln pV/ p₀V₀ = α [(1/pV) - (1/p₀V₀)] ↔ ↔ ln(V/V₀) (pV/p₀V₀) ^{1/(γ -1)} = α [(1/pV) - (1/p₀V₀)]. (3.8)

Производим потенцирование (3.8) и получаем следующее выражение уравнение процесса в параметрах P давленияи V объёмадля одного моляидеального газа, у которого C молярная теплоёмкость зависит от T температурыэтого идеального газа в соответствии с C = α/T выражением:

(V/V₀)(PV/P₀V₀) ^{1/(γ -1)} = e^α/PVe^-α/P0V0 ↔ (V/V₀) ^{γ -1}(PV/P₀V₀) = e^{α(γ -1)/PV}e^{-α(γ -1)/P0V0} ↔ PV ^γe^{-α(γ -1)/PV} = const,(3.9)

где const = P₀V₀ ^γ e^{-α(γ -1)/P0V0} - постоянное значение, получаемое подстановкой в выражение const начальных P₀,V₀ соответственнодавления,объёма, связанных с начальной T₀ температурой уравнением (4.13) из раздела 04.1.0 "Физическая термодинамика" Клапейрона –Менделеевадля одного моляидеального газа: T₀ = P₀V₀/R.

Произведение P₀V₀ начальных давления и объёмаили начальной T₀ температурыодного моляидеального газа для определения уравнение процесса в параметрах P давленияи V объёма должно задаваться в условии задачи.

Задача 04.1.1.4

Определить количество поглощённого Q тепла при расширении одного моля реального газа от V₁ до V₂ величины объёма, если T температура этого газа при расширении постоянна.

Газ считать ван-дер-ваальсовским. Дано: V₁; V₂; ν = 1 моль / Q = ?

Поскольку T температура ван-дер- ваальсовского газа при расширении постоянна, т.е. dT = 0, то (4.1) дифференциал dU внутреннейэнергии принимает следующий вид: dU = (a/V²)dV. (4.2) Уравнение (4.13) из раздела 04.1.0 "Физическая термодинамика" Клапейрона – Менделеевадля одного моля эквивалентногоидеального газа имеет следующий вид: P'V' = RT,(4.3)

где P′, V′ - соответственно(рис. 04.1.1.4)давление(4.109)из раздела 04.1.0 "Физическая термодинамика" и объём(4.110) из раздела 04.1.0 "Физическая термодинамика" идеальногогаза, эквивалентногопо своим свойствам ван - дер - ваальсовскому газус P давлениемна стенки сосудаи V объёмом;

T - температура ван-дер-ваальсовского газа, равная T температуреэквивалентногоидеального газа.

Подставляем в (4.2) P′ = P + (a/V ²) давление(4.109)из раздела 04.1.0 "Физическая термодинамика", V′ = V - bобъём(4.110) из раздела 04.1.0 "Физическая термодинамика" эквивалентного идеальногогаза и получаем следующее выражение (рис. 04.1.1.4) Pдавленияна стенки сосуда одного моляван-дер-ваальсовского газа, имеющего T температуру:

[P + (a/V ²)](V - b) = RT ↔P = [RT/(V - b)] - (a/V²). (4.4)ЭлементарнаяδA = PdV работа (4.12) из раздела 04.1.0 "Физическая термодинамика", выполненная одним молемгаза Ван - дер - Ваальса, с учётом (4.4) выражения Pдавленияна стенки сосуда этогогазаВан - дер - Ваальса, имеющего T температуру, имеет следующий вид: δA = PdV = [RT/(V - b)]dV - (a/V²)dV, (4.5)где b - постоянная, определяемая физико - химическими свойствами молекул газа.

Согласно (4.10) из раздела 04.1.0 "Физическая термодинамика" первым началом термодинамикив интегральном видеQ₁₂ теплота дляперевода термодинамическойсистемы

(рис. 04.1.1.4) из 1-ого состояния с V₁ объёмомво 2-ое состояние с V₂ объёмомс учетом (4.2) и (4.5) имеет следующий вид:

2 2 2 V₂ V₂

Q₁₂ = ∫ δQ = ∫ dU + ∫ δA ↔ Q₁₂ = ∫ (a/V²)dV + ∫ [RT/(V - b)]dV - (a/V²)dV ↔

1 1 1 V₁ V₁

↔ Q₁₂ = RT ln[(V₂ - b)/(V₁ - b)].(4.6)

Задача 04.1.1.5

Найти для одного моляван-дер-ваальсовского газа уравнение адиабатического процесса в параметрах T температурыи V объёма, у которого известна C_V молярная теплоемкость этого ван-дер- ваальсовского газа при V постоянном объеме.

ван - дер - ваальсовскому газус P давлениемна стенки сосудаи V объёмом; T - температура ван-дер-ваальсовского газа, равная T температуреэквивалентногоидеального газа.

Подставляем в (4.1) P′ = P + (a/V ²) давление(4.109)из раздела 04.1.0 "Физическая термодинамика", V′ = V - bобъём(4.110) из раздела 04.1.0 "Физическая термодинамика" эквивалентного идеальногогаза и получаем следующее выражение Pдавленияна стенки сосуда одного моляван-дер-ваальсовского газа, имеющего T температуру: [P + (a/V ²)](V - b) = RT ↔

P = [RT/(V - b)] - (a/V ²). (5.2)

Изменение dU внутреннейэнергии газа Ван - дер - Ваальсасогласно первому началутермодинамики (4.113) из раздела 04.1.0 "Физическая термодинамика" в дифференциальномвиде для адиабатическогопроцесса принимает следующий вид: dU = - δA ↔ dU = - PdV. (5.3)

где dU - дифференциалвнутреннейэнергии газа Ван- дер- Ваальса(4.116) из раздела 04.1.0 "Физическая термодинамика", выполненная газом Ван- дер- Ваальса.

Дифференциал dU внутреннейэнергии одного молягаза Ван- дер- Ваальса(4.116) из раздела 04.1.0 "Физическая термодинамика" имеет следующий вид:

dU = (∂U/∂T)dT + (∂U/∂V)dV = {∂[C_VT - (a/V)]/∂T}dT + {∂[C_VT - (a/V)]/∂V}dV = C_V dT + (a/V²)dV. (5.4)

ЭлементарнаяδA = pdV работа (4.12) из раздела 04.1.0 "Физическая термодинамика", выполненная одним молемгаза Ван - дер - Ваальса, с учётом (5.2) выражения Pдавленияна стенки сосуда этогогазаВан - дер - Ваальса, имеющего T температуру, имеет следующий вид: δA = PdV = [RT/(V - b)]dV - (a/V ²)dV. (5.5)

Подставляем (5.4) дифференциал dU внутреннейэнергии и (5.5) элементарную

δA = pdV работу в выражение (5.3) первого началатермодинамики в дифференциальномвиде для адиабатическогопроцесса и получаем следующее дифференциальное уравнение с разделяющимися переменными относительно параметров T температурыи V объёма одного молягаза Ван - дер - Ваальса: C_V dT + (a/V)²dV = - [RT/(V - b)]dV + (a/V ²)dV ↔ dT/T = - R/C_V dV/(V - b). (5.6)

Производим интегрирование (5.6) от начального V₀ доконечногопеременного Vобъёма газа Ван - дер - Ваальса, которым соответствует начальная T₀ и конечнаяпеременная T температура, после чего получаем следующее уравнение процесса в параметрах T температуры и V объёмадля одного моляэтогогаза Ван - дер - Ваальса, у которого молярная теплоемкостьпри V постоянном объеме равна C_V: T V

∫dT/T = - R/C_V ∫dV/(V - b) ↔ ln (T/T₀) = ln[(V - b)/(V₀ - b)]^-αR/CV ↔ T₀ V₀

↔ T/T₀ = [(V - b)/V₀]^{- α} ↔ T(V - b) ^α = T₀ (V₀ - b) ^α = const, (5.7)

где α = R/C_V.

Начальные T₀,V₀ соответственнотемпературы,объёма одного молягаза Ван - дер - Ваальса для определения уравнение процесса в параметрах T температуры и V объёма должно задаваться в условии задачи.