Элементы релятивистской механики

Преобразования Галилея

Понятие событиеи инерциальная система отсчётаявляются основополагающими во всех физических процессах.

Событиеопределяется как физическое явление, происходящее в какой-либо области пространства в некоторый момент времени в избранной системе отсчёта. Таким образом, событиехарактеризуется своим физическим содержанием, местом и временем.

Инерциальной системой отсчёта(ИСО) по аналогии с параграфом «Динамика поступательного движения в инерциальных системах отсчета»израздела 01.0.0 «Физические основы механики»называется такая система отсчёта, в которой материальная точкаили механическая система, свободная от внешних воздействий, покоится или движется равномернои прямолинейно.

ПреобразованияГалилея, выражающее пространственно- временнуюсвязь любого события в разных ИСО,применяютсяв ньютоновой механикепри переходе от одной K(x,y,z,t)неподвижнойИСО к другой K′(x′,y′,z′,t′) подвижнойИСО, которая движется относительно K(x,y,z,t) поступательно с вектором v постоянной скорости. Преобразования Галилеяосновываются на аксиомах об абсолютности промежутков времении длин. Первая аксиома утверждает, что ход времени, т.е. промежуток временимежду двумя какими-либо событиями, одинаков во всех ИСО.

из O′ начала координат в произвольнуюMточкупространства, связан сr радиусом - вектором, направленным из O начала координат K(x,y,z,t) неподвижнойИСО в ту же Mточкупространства, с учетом (3.1) следующим выражением: r′ = r - r₀′ = r - vt ↔ x′ = x - v_x′t; y ′ = y - v_y′ t; z′ = z - v_z′t, (3.2) где x, y, z и x′, y′, z′ - соответственно координаты M точки в K(x,y,z,t) неподвижнойИСО в момент

t времени и в K′(x′,y′,z′,t′) подвижнойИСО в момент времени t′ = t, r и r′ - радиусы- векторыM точки в тех же системах отсчета, а v_x′, v_y′ и v_z′- проекциина оси координатK(x,y,z,t) неподвижнойИСО вектораv скорости постояннойскорости, с которым K′(x′,y′,z′,t′) подвижнаяИСО движется относительно K(x,y,z,t) неподвижной ИСО. Таким образом, координаты точки в K′(x′,y′,z′,t′) подвижнойИСО и K(x,y,z,t) неподвижнойИСОсвязаны преобразованиями (3.2)Галилея. Согласно преобразованиям (3.2)ГалилеявK′(x′,y′,z′,t′) подвижнойИСО и K(x,y,z,t) неподвижнойИСОвремяt′ и t совпадают, а координаты произвольной точки в K′(x′,y′,z′,t′) подвижнойИСОможноопределить, зная координаты этой произвольной точки в K(x,y,z,t) неподвижнойИСО, а также зная v_x′, v_y′ и v_z′ - проекциина оси координатK(x,y,z,t) неподвижнойИСО вектораv скорости постояннойскорости, с которым K′(x′,y′,z′,t′) подвижнаяИСО движется относительно K(x,y,z,t) неподвижнойИСО.

Инвариантность уравнений механики относительно преобразований Галилея

При движении K′(x′,y′,z′,t′) подвижнойИСО(рис. 03.0.2) вдоль положительного направления

OY осиK(x,y,z,t) неподвижнойИСО с векторомvпостоянной скорости с учетом равенства нулюпроекций вектора v скоростина OX и OZ оси, т.е. v_x′ = 0, v_z′ = 0, выражения (3.2) принимают следующий вид: x′ = x; y ′ = y - vt; z′ = z и t′ = t.(3.3)

dz′/dt = dz/dt ↔ v_Z ′ = v_Z, (3.6)

где v - модуль вектора v скоростидвижения K′(x′,y′,z′,t′) подвижнойИСО (рис.3.2) вдоль положительного направления OYосиK(x,y,z,t) неподвижнойИСО.

Проекции (рис. 03.0.2) dv_X ′/dt, dv_Y ′/dt и dv_Z ′/dt вектора a′_M ускорения материальной M точки на оси K′(x′,y′,z′,t′) подвижнойИСОсогласно (3.4), (3.5) и (3.6) равны проекциям dv_X /dt, dv_Y /dt и dv_Z /dt вектора a_M ускорения этой материальной M точки на оси в K(x,y,z,t) неподвижнойИСО,т.е.

dv_X ′/dt = dv_X /dt; dv_Y ′/dt = dv_Y /dt и dv_Z ′/dt = dv_Z /dt, поэтому векторы ускорения a′_M и a _M материальной M точки соответственно в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО равны друг другу, вследствие чего имеет место следующее выражение: a′_M = a_M .(3.7) Согласно (3.7) вектор a_M ускорения материальной M точки не зависит от выбора ИСО, т.е. этот вектор a ускорения инвариантенотносительно преобразованийГалилея.

инвариантнопо отношению к ИСО.

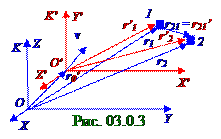
Векторы dr′₁/dt = v′₁ и dr′₂/dt = v′₂ (1.4)из раздела 01.0 "Физические основы механики" скоростейматериальных1 и 2 точек в K′(x′,y′,z′,t′) подвижнойИСОи векторы dr₁/dt = v₁ и dr₂/dt = v₂ скоростей при перемещении этих же материальныхточек в K(x,y,z,t) неподвижнойИСО с учётом выражений (3.2) преобразованийГалилея имеют следующий вид:

v₁ = dr₁/dt ; v₂ = dr₂/dt; v′₁ = dr₁/dt - v;v′₂ = dr₂/dt - v, (3.9) где (3.1) v=dr₀′/dt - вектор скорости перемещения O′ начала координат K′(x′,y′,z′,t′) подвижнойИСОотносительно K(x,y,z,t) неподвижнойИСО.

С использованием выражения (3.9) произведём вычитание v₂ -v₁ и v′₂ -v′₁ и получим следующие выражения вектора v₂ -v₁ скорости движенияматериальной2 точки относительно материальной

1 точки в K(x,y,z,t) неподвижнойИСО и векторv′₂ -v′₁ скорости движения этой материальной

2 точки относительно материальной1 точки в K′(x′,y′,z′,t′) подвижнойИСО: v₂ -v₁ = v′₂ -v′₁. (3.10) Согласно (3.10) относительные скорости движения материальныхточек не зависят от выбора ИСО, т.е. инвариантны к ИСО.

Согласно (3.7) вектор a_M ускорения материальной M точки не зависит от выбора ИСО, поэтому согласно (1.45)из раздела 01.0.0 "Физические основы механики", вектор F силы, пропорциональный вектору a ускорения, и второй законНьютона не зависят от выбора ИСО, т.е. инвариантен к ИСО. Распространив доказательства на все законы ньютоновойили классической механикиможно сделать вывод, что в классической механикесправедлив механический принцип относительности: законы классической механики одинаковы во всех ИСО.

Специальная теория относительности. Постулаты Эйнштейна

Обобщение принципа относительностина все физические явлениябыло осуществлено А.Эйнштейномв специальной теории относительности(СТО). Координаты и время в различных ИСО связаны преобразованиямиЛоренца, а не Галилея. Однако при малых скоростях относительного движения систем отсчета по сравнению со скоростями света в вакууме преобразования Лоренца переходятв преобразованияГалилея. СТОназывают релятивистской теориейот английского слова"relativity", что означает относительность.Релятивистскиеэффекты проявляются при скоростях движения тел, близких по величине к c = 3·10⁸ м/с скорости светав вакуумеи называемых релятивистскимискоростями. Релятивистский принцип относительностиЭйнштейна: в любых ИСО все физическиеявления при одних и тех условиях, но при разныхскоростях движенияИСО, протекают одинаково. Иначе: физические законы независимы, т.е.инвариантны, по отношению к выбору ИСО.

Принцип инвариантности скорости света: скорость света в вакууме не зависит от движения источника света. Она одинакова во всех направлениях и во всех инерциальных системах. Постулаты СТОпротиворечат утверждению механикиНьютона об одинаковости хода времениво всех ИСО и, следовательно, обабсолютности промежуткавремени между двумя какими-либо событиями.

К моменту времени t₁ > 0 свет, распространяясь в вакууме со c скоростью, достигнет в K(x,y,z,t) неподвижнойИСО точек поверхности сферы с O центром в точке и ct₁ радиусом. Так как согласно постулату СТОскорость света не зависит от движения источника света, светв K′(x′,y′,z′,t′) подвижнойИСО к моменту времени t₁′ = t₁ > 0 достигнет точек сферы того же ct₁ радиуса, что и в K(x,y,z,t) неподвижнойИСО, но с O′ центром в точке, находящейся в это время не в O точке, а на расстоянии vt₁ от неё. Векторv скорости K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО направлен по OY оси этой K(x,y,z,t) неподвижнойИСО.

Соединение постулата СТОо том, что c скорость света в вакууме не зависит от движения источника света, с классическимпредставлением о времени, идущем одинаково во всех системах отсчета, приводит к абсурду- светвспышки должен одновременно достигать точек пространства, принадлежащих двум разным сферам.

Преобразования Лоренца

Преобразования Лоренцаустраняют противоречия между ньютоновойи релятивистскоймеханикой, вследствие того, что позволяют установить связь между координатами и временемсобытия, происшедшего в K′(x′,y′,z′,t′) подвижнойИСО и двигающейся относительно K(x,y,z,t) неподвижнойИСО, скоординатами и временемтого же события в этой K(x,y,z,t) неподвижнойИСО.

Если K′(x′,y′,z′,t′) подвижнаяИСО (рис. 03.0.2) перемещается вдоль положительного направления OYосиотносительно K(x,y,z,t) неподвижнойИСО с модулём v вектора v скорости, то x', y', z′; x, y, z координаты произвольнойM точки пространства в неподвижнойИСО и t′; t время соответственно в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО связаны между собой частными преобразованиямиЛоренца, имеющими следующий вид:

x′ = x ↔ x = x′; z′ = z ↔ z = z′;

y′ = (y - vt)/[1-(v²/c²)]^1/2 ↔ y = (y′ + vt′)/[1-(v²/c²)]^1/2; (3.11) t′ = [t - (vy/c²)]/[1-(v²/c²)]^1/2 ↔ t = [t′+ (vy′/c²)]/ [1-(v²/c²)] ^1/2,

где при выводе этих (3.11)частных преобразованийЛоренца предполагалось, что в начале движения K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО, т.е. при t′₀ = t₀ = 0, O′ начало (рис.3.2) координат K′(x′,y′,z′,t′) подвижнойИСО совпадает сO началом координатK(x,y,z,t) неподвижнойИСО. С учётомэтихначальных условий по аналогии с (3.3) преобразованиями Галилея связь y′ координаты (рис. 03.0.2) произвольной M точки пространства вK′(x′,y′,z′,t′) подвижнойИСО с y координатой этой произвольной M точки пространства в неподвижной K(x, y, z, t) ИСОимеет следующий вид: y′ = α(y - vt), (3.12) где α - подлежащий определению коэффициент, который может зависеть от v модуля вектора

v скорости движения (рис. 03.0.2) K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО, но не от координат x', y', z′; x, y, z произвольнойM точки пространства и t′; t времени соответственно в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО. Для преобразований

(3.3) Галилеяэтот α коэффициентравен единице, т.е. α = 1.Уравнение (рис.3.2) движения O начала координат K(x,y,z,t) неподвижнойИСО относительно K′(x′,y′,z′,t′) подвижнойИСО имеетследующий вид: y′_O = - vt′. (3.13)

Связь y координаты (рис. 03.0.2) произвольной M точки пространства по OY оси координат в K(x,y,z,t) неподвижнойИСО с y' координатой этой же произвольной M точки пространства по O'Y' оси координатв K′(x′,y′,z′,t′) подвижнойИСО по аналогии с (3.12) имеет следующий вид:

y = β(y' + vt′), (3.14) где β - подлежащий определению коэффициент, который может зависеть от v модуля вектора

v скорости движения (рис. 03.0.2) K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО, но не от координат x', y', z′; x, y, z произвольнойM точки пространства и t′; t времени соответственно в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО. Для преобразований

(3.3) Галилеяэтот βкоэффициентравен единице, т.е. β = 1.

Решаем уравнения (3.12), (3.14) относительно t′ времени в K′(x′,y′,z′,t′) подвижнойИСО с помощью исключения из выражений (3.12), (3.14) y' координаты K′(x′,y′,z′,t′) подвижнойИСО, вследствие чего получаем следующее выражение: t′ = α{t - (y/v)[1 - (1/αβ)]}. (3.15)

Для определения α, βкоэффициентов в выражениях (3.12), (3.14) в эксперименте (рис.3.4) учтём отличия t′; t временисоответственно в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО и принцип инвариантности скорости света, согласно которому c скорость света в вакууме одинакова (рис. 03.0.4) в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО. К моменту времени t₁ > 0 в K(x,y,z,t) неподвижнойИСО свет, распространяясь в вакууме со c скоростью, достигнет точки со следующей y₁ координатой: y₁ = ct₁. (3.16) С учётом принципа инвариантностиcскорости света и учётом того, что в момент t₁ времени в K(x,y,z,t) неподвижнойИСО в K′(x′,y′,z′,t′) подвижнойИСО будет момент времени t′₁, в который свет, распространяясь в вакууме со c скоростью, окажется в этой K′(x′,y′,z′,t′) подвижнойИСО в следующей y₁' координате: y₁' = ct′₁.(3.17) Возводим левую и правую (3.16), (3.17) части в квадрат.Вычитаем квадратвыражения(3.17) из квадрата выражения(3.16) и получаем следующее выражение:

y₁² - (y₁')² = (ct₁)²- (ct′₁)²↔ y₁² - (ct₁)² - (y₁')²+ (ct′₁)²= 0.(3.18) Подставляем выражения (3.15) t′ времени и (3.12) y′ координаты в K′(x′,y′,z′,t′) подвижнойИСО в выражение (3.18) и получаем квадратное уравнение относительно неизвестных (3.12), (3.14) α, β коэффициентов, в котором для общего случая моменты (3.16), (3.17) времени t₁ и t′₁ заменены их произвольными значениями t и t′, но с условием, что произвольному значению t времени в K(x,y,z,t) неподвижнойИСО соответствует значение t′ времени в K′(x′,y′,z′,t′) подвижнойИСО, вследствие чего это квадратное уравнение относительно неизвестных (3.12), (3.14) α, β коэффициентовимеет следующий вид: y² - (ct)² - α²(y - vt)² + c²α²{t - (y/v)[1 - (1/αβ)]}² = 0. (3.19) После возведения в выражении (3.19) слагаемых в квадрат и их группировки получаем следующее выражение: t²[- c² - α²v²+ α²c²] + 2yt[α²v - (α²c²/v) + (c²α/vβ)] + + y²[1 - α² + (α²c²/v²) + (c²/v²β ²) - (2c²α/v²β] = 0. (3.20) Координата y произвольной M точки пространства в K(x,y,z,t) неподвижнойИСО никак не связана с произвольным t моментом времени в этой же K(x,y,z,t) неподвижнойИСО, т.е. уравнение (3.20) должно выполняться при любых значениях y координаты и t времени, что возможно при равенстве нулю коэффициентов в уравнении (3.20) упараметров t², yt и y², вследствие чего имеют место следующие выражения: - c² - α²v²+ α²c² = 0; (3.21)

α²v - (α²c²/v) + (c²α/vβ) = 0;(3.22)

1 - α² + (α²c²/v²) + (c²/v²β ²) - (2c²α/v²β) = 0.(3.23) Из решения (3.21) уравнения относительно (3.12) α коэффициента следует выражение: α = 1/[1 - (v²/c²)]^1/2.(3.24) Подставляем выражение (3.24) α коэффициентав выражение (3.22) и получаем следующее значение β коэффициента, которое оказывается равным значению α коэффициента: β = 1/[1 - (v²/c²)]^1/2.(3.25) Подставляем выражение (3.24) α коэффициентав выражение (3.12) и получаем связь (3.11)

y′ координаты (рис. 03.0.2) произвольной M точки пространства K′(x′,y′,z′,t′) подвижнойИСО с

y координатой этой же произвольной M точки пространства и tвременем в K(x,y,z,t) неподвижнойИСО, которая имеет следующий вид: y′ = (y - vt)/[1-(v²/c²)]^1/2, (3.26) где v - модуль вектора v скорости движения (рис. 03.0.2) K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направлении OY оси.

ПодвижнаяK′(x′, y′, z′, t′)ИСО (рис.3.2) перемещается вдоль положительного направления OY оси относительно K(x,y,z,t) неподвижнойИСО, а по OX и OZ осям эта K′(x′,y′,z′,t′) подвижнаяИСО неподвижна, поэтому координаты x′, z′ произвольной M точки пространства в K′(x′,y′,z′,t′) подвижнойИСО равны (3.11) координатам x, z этой же произвольной M точки пространства в K(x,y,z,t) неподвижнойИСО, вследствие чего имеют место следующие выражения: x′ = y; z′ = z.(3.27) Подставляем выражения α (3.24) и β (3.25) коэффициентовв выражение (3.15) и получаем выражение (3.11) связи t′ времени в K′(x′,y′,z′,t′) подвижнойИСО с t временем в K(x,y,z,t) неподвижнойИСО, которое имеет следующий вид: t′ = [t - (vy/c²)]/[1-(v²/c²)]^1/2, (3.28) Согласно выражению (3.28) определённому моменту t времени наступления события в

K(x,y,z,t) неподвижнойИСО соответствует множество моментов t′ времени наступления события в K′(x′,y′,z′,t′) подвижнойИСО в зависимости от y координаты, в которой это событие наступает в K(x,y,z,t) неподвижнойИСО, и модуля v вектора v скорости (рис. 03.0.2) движения K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направлении OY оси. Решаем уравнение (3.28) относительно t времени и получаем связь этого t времени в K(x,y,z,t) неподвижнойИСО с t′ временем в K′(x′,y′,z′,t′) подвижнойИСО, которая имеет следующий вид: t = t′[1-(v²/c²)]^1/2 + (vy/c²), (3.29) где v - модуль вектора v скорости движения (рис. 03.0.2) K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направления OYоси; y -координата произвольной

M точки пространства вK(x,y,z,t) неподвижнойИСО.

Подставляем выражение (3.29) в выражение (3.26), решаем полученное уравнение относительно y координаты и получаем (3.11) связь y координаты произвольной M точки пространства вK(x,y,z,t) неподвижнойИСО с y′ координатой (рис. 03.0.2) той же произвольной M точки пространства по O′Y' оси координат и временем t′ в K′(x′,y′,z′,t′) подвижнойИСО, которое имеет следующий вид:

y = (y' + vt')/[1-(v²/c²)]^1/2, (3.30)Подставляем выражение (3.30) в выражение (3.29), решаем полученное уравнение относительно

t времени и получаем (3.11) связь t времени в K(x,y,z,t) неподвижнойИСО с t′ временем и

y′ координатой (рис. 03.0.2) произвольной M точки пространства в K′(x′,y′,z′,t′) подвижнойИСО, которое имеет следующий вид: t = [t′ + (vy′/c²)]/[1-(v²/c²)]^1/2, (3.31) где v - модуль вектора v скорости движения (рис.3.2) K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направления OYоси.

Согласно выражению (3.31) определённому моменту t′ времени наступления события в K′(x′,y′,z′,t′) подвижнойИСО соответствует множество моментов t времени наступления события в K(x,y,z,t) неподвижнойИСО в зависимости от y′ координаты, в которой это событие наступает в K′(x′,y′,z′,t′) подвижнойИСО, и модуля v вектора v скорости (рис. 03.0.2) движения K′(x′,y′,z′,t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направлении OYоси.

Координатное кинематическое следствие из преобразований Лоренца

Линейный размер тела,движущегося относительно K(x,y,z,t) неподвижнойИСО, уменьшается в направлении движения. Стержень Ст (рис. 03.0.5) покоится в K′(x′,y′,z′,t′) подвижнойИСО. Его длина имеет величину l₀ = y₂′ - y₁′, где y₂′ и y₁′ - координаты концов Ст стержня в K′(x′,y′,z′,t′) подвижнойИСО, относительно которой он покоится. Длина l = y₂ - y₁ того же Ст стержня в K(x,y,z,t) неподвижнойИСО, относительно которой K′(x′,y′,z′,t′) подвижнаяИСО движется вместе со Ст стержнем в положительном направлении OYоси с вектором v скорости, измеренная в этойK(x,y,z,t) неподвижнойИСО в момент t времени, имеет следующий вид:

l = y₂ - y₁ = {y′₂[1-(v²/c²)]^1/2} + vt - {y′₁[1-(v²/c²)]^1/2} - vt = (y′₂ - y′₁)[1-(v²/c²)]^1/2 = l₀ [1-(v²/c²)]^1/2, (3.32)

y′₁ начальную и y′₂ конечнуюкоординаты этого Ст стержня в K′(x′,y′,z′,t′) подвижнойИСО.

Поперечныеh и d размеры Ст стержня одинаковы по O′X′ и O′Z′ осям координат в K′(x′,y′,z′,t′) подвижнойИСО, относительно которой он покоится, с поперечнымиh и d размерами того же

Ст стержня по OX и OZ осям координат в K(x,y,z,t) неподвижнойИСО, т.к. этот Ст стержень перемещается в K′(x′,y′,z′,t′) подвижнойИСО относительноK(x,y,z,t) неподвижнойИСО только в положительном направлении OYоси,вследствиечегодля этихh и d размеров имеет место следующее выражение: d = x₂′ - x₁′ = x₂ - x₁ и h = z₂′ - z₁′ = z₂ - z₁. (3.33) Так как согласно(3.32) длина l₀ = y₂′ - y₁′ покоящегося Ст стержня вK′(x′,y′,z′,t′) подвижнойИСОбольшедлины l = x₂ - x₁ этого Ст стержня вK(x,y,z,t) неподвижнойИСО, относительно которой Ст стержень движется в положительном направлении OY оси с вектором v скорости, т.е. l₀ > l, то в релятивистской механике существует следующее правило: линейные размеры тела, называемые собственнымиразмерами этого тела,максимальны в той ИСО, относительно которой тело покоится.

Временное кинематическое следствие из преобразований Лоренца

Согласно (3.28) одному моментуt_k временив K(x,y,z,t) неподвижнойИСО(рис. 03.0.5) соответствует множество значенийt_i′ в K′(x′,y′,z′,t′) подвижнойИСОв зависимости от значения

y_kкоординаты материальной точки в K(x,y,z,t) неподвижнойИСОи модуля v вектора v скорости (рис. 03.0.2) движения K′(x′,y′,z′,t′) подвижнойИСОотносительно K(x,y,z,t) неподвижнойИСОв положительном направлении OYоси, вследствие чего имеет место следующее выражение:

t_i′ = [t_k - (vy_k /c²)]/[1-(v²/c²)]^1/2. (3.34) Согласно (3.31) одному моментуt_i′ временив K′(x′,y′,z′,t′) подвижнойИСО(рис. 03.0.5) соответствует множество значенийt_k времени в K(x,y,z,t) неподвижнойИСО в зависимости от значения координаты y_i′ материальной точки в K′(x′,y′,z′,t′) подвижнойИСОи модуля v вектора v скорости (рис. 03.0.2) движения K′(x′,y′,z′,t′) подвижнойИСОотносительно K(x,y,z,t) неподвижнойИСО в положительном направлении OXоси, вследствие чего имеет место следующее выражение: t_k = [t′_i + (vy′_i /c²)]/[1-(v²/c²)]^1/2. (3.35)

В движущейся в положительном направлении OYоси (рис. 03.0.6) с вектором v скорости K′(x′,y′,z′,t′) подвижнойИСОотносительноK(x,y,z,t) неподвижнойИСО в момент t′_i времени происходит в A точке c y_i′ координатой появление мишени - окружности, что представляет собой

1- е событие, а в момент t′_i+1 временипроисходит 2- е событие в той же A точке c y_i′ координатой: попадание пулив мишень - окружность.

Промежутоквремени τ₀ между 1-ым и 2-ым событиями вK′(x′,y′,z′,t′) подвижнойИСО,в которой эти событияпроисходятв одной и той же A точке c y_i′ координатой, найдётся из следующего выражения: τ₀ = t′_i+1 - t′_i . (3.36)

В K(x,y,z,t) неподвижнойИСО 1- е событие, т.е. появление мишени,и 2- е событие, т.е. попадание пули в мишень, совершаются в разных точках пространства с y_k и y_{k +1} координатами, причем y_{k +1} - y_k = vτ,где τ = t_k+1 - t_k - промежутоквременимежду1- ым и 2-ым событиями по часамв K(x,y,z,t) неподвижнойИСО, а vτ - расстояние, на которое переместитсяK′(x′,y′,z′,t′) подвижнаяИСОза τ промежутоквремениотносительноK(x,y,z,t) неподвижнойИСО в положительном направлении OYоси.

Подставляем в (3.35) выражение промежуткаτ = t_k+1 - t_kвремени величины моментов t_k и t_k+1 временинаступления 1- ого и 2-ого событий в K(x,y,z,t) неподвижнойИСО, выраженных через соответствующие моменты t_i′, t_i+1′ времени наступления этих 1- ого и 2-ого событий по часамвK′(x′,y′,z′,t′) подвижнаяИСО, и получаем выражение этого промежуткаτ = t_k+1 - t_kвремени по часамв K(x,y,z,t) неподвижнойИСО, которое имеет следующий вид: τ = t_k+1 - t_k =

=[t_i+1′+ (vy_i′)/c²)]/[1-(v²/c²)]^1/2 - [t_i′+ (vy_i′)/c²)]/[1-(v²/c²)]^1/2 = (t_i+1′ - t_i′)/[1-(v²/c²)]^1/2 = τ₀/[1-(v²/c²)]^1/2, (3.37)

K′(x′,y′,z′,t′) подвижнаяИСО движется в положительном направлении OYоси с вектором v скорости, т.е. τ₀ < τ, то в релятивистской механике существует правило: промежуток времени между двумя событиями минималенв той ИСО, в которой оба событиясовершаются в одной и той же координатеэтойИСО. Время, измеряемое по часам, движущимся вместе с данным объектом, называется собственным временемэтого объекта.

Релятивистский эффект замедленияхода времени в K′(x′, y′, z′, t′) подвижнойИСО по сравнению с K(x,y,z,t) неподвижнойИСО заключается в следующем: часы, движущиеся с вектором v скорости относительно K(x,y,z,t) неподвижнойИСО, идут медленнеев 1/[1-(v²/c²)]^{1/ 2} раз, чем часы, находящиеся в этойK(x,y,z,t) неподвижнойИСО. Все физическиепроцессы в K′(x′, y′, z′, t′) подвижнойИСО протекают медленнее, чемв K(x,y,z,t) неподвижнойИСО. Релятивистский закон сложения скоростей. Интервал между двумя событиями в релятивистской механике. Элементы релятивистской динамики: основное уравнение релятивистской динамики. Кинетическая энергия релятивистской частицы. Взаимосвязь массы и полной энергии релятивистской частицы. Связь между импульсом и полной энергией релятивистской частицы. Система невзаимодействующих релятивистских частиц: столкновение, энергия и импульс

раздела 01.0.0 "Физические основы механики" соответственно в K′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО.

Пусть K′(x′, y′, z′, t′) подвижнаяИСО перемещается с вектором v скорости (рис. 03.0.7) в положительном направлении OYосиотносительно K(x,y,z,t) неподвижнойИСО. При этом проекции v_X, v_Z вектора v скорости (рис. 03.0.7) движения K′(x′, y′, z′, t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО равны нулю, т.е.v_X = 0, v_Z = 0, а также равны начальные моменты времениt₀ = t₀′ = 0 в обеих системах координат и совпадаютвначальный момент времениO и O′ началакоординатсоответственноK′(x′,y′,z′,t′) подвижнойи K(x,y,z,t) неподвижнойИСО. Тогда перемещение материальной M точкина элементарныеdx_M, dy_M и dz_Mприращениев K(x,y,z,t) неподвижнойИСО приводит к элементарным приращениям dx′_M, dy′_M и dz′_M этой же материальной M точкив K′(x′, y′, z′, t′) подвижнойИСО.

Связь между элементарными приращениями dx_M, dy_M, dz_M, dt при перемещении материальной M точкив K(x,y,z,t) неподвижнойИСО и соответствующими элементарнымиприращениями dx′_M, dy′_M, dz′_M, dt′, возникающие у этой же материальной M точкивK′(x′, y′, z′, t′) подвижнойИСО, устанавливается частными(3.11) преобразованиями Лоренца, вследствие чего имеют место следующие выражения: 1) dx_M = dx′_M; 2) dy_M = (dy′_M + vdt′)/[1-(v²/c²)]^1/2; 3) dz_M = dz′_M; 4) dt = [dt′+ (vdy′_M /c²)]/[1-(v²/c²)]^1/2, (3.39) где v- модуль вектора v скорости, с которойK′(x′, y′, z′, t′) подвижнаяИСО перемещается в положительном направлении OY оси относительно K(x,y,z,t) неподвижнойИСО.

Разделив второеиз равенств в (3.39) на четвертое, получимвыражениеv_MY проекции на OY осьвектора v_Mскоростиматериальной M точки (рис. 03.0.7) в K(x,y,z,t) неподвижнойИСО, приводящей к наличию v_{MY ′} проекции на O′Y' ось вектора v′_Mскороститой жематериальной M точки (рис. 03.0.2)в

K′(x′, y′, z′, t′) подвижнойИСО и имеющей следующий вид: v_MY = dy_M /dt =

= (dy′_M + vdt′)/[dt′+ (vdy′_M/c²)] = [(dy′_M/dt′) + v]/[1 + (dy′_M/dt′)(v/c²)] = (v_{MY ′} + v)/[1 + (vv_{MY ′}/c²)], (3.40)

где v - модуль вектора v скорости движения (рис. 03.0.2) K′(x′, y′, z′, t′) подвижнойИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направления OYоси.

Разделив первоеи третьеиз равенств в (3.39) на четвертое получимвыраженияv_MX, v_MZ проекций на OX и OZ осивектора v_Mскоростиматериальной M точки (рис. 03.0.2) в K(x,y,z,t) неподвижнойИСО, приводящие к наличию соответственно v_{MX ′}, v_{MZ ′} проекций на O′X′ и O′Z′ оси вектора v′_Mскороститой жематериальной M точки (рис. 03.0.7)в K′(x′, y′, z′, t′) подвижнаяИСО и имеющие следующий вид:v_MX = dx/dt = v_{MX ′} [1-(v²/c²)]^1/2/[1 + (vv_{MY ′}/ c²)]; v_MZ = dz/dt = v_{MZ ′} [1-(v²/c²)]^1/2/[1 + (vv_{MY ′}/c²)],(3.41) где v - модуль вектора v скорости движения (рис. 03.0.2) K′(x′, y′, z′, t′) подвижнаяИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направлении OXоси; v_{MY ′}- проекция на O′Y' ось вектора v′_Mскоростиматериальной M точки (рис. 03.0.7)в K′(x′, y′, z′, t′) подвижнаяИСО

В (3.40) и (3.41) выразим v_{MX ′}, v_{MY ′}, v_{MZ ′} через v_MX, v_MY, v_MZ и получим проекции

v_{MX ′}, v_{MY ′}, v_{MZ ′} на O′X' , O′Y′, O′Z′ осивектора v′_Mскоростиматериальной M точки (рис.3.7)в

K′(x′, y′, z′, t′) подвижнойИСО, являющиеся следствием движенияс проекциями v_MX, v_MY, v_MZ на OX, OY, OZ осивектора v_Mскорости той жематериальной M точки в K(x,y,z,t) неподвижнойИСО и имеющие следующий вид: v_{MX ′} = v_MX [1-(v²/c²)]^1/2/[1 - (vv_MY /c²)]; v_{MY ′} = (v_MY - v)/[1 - (vv_MY /c²)]; v_{MZ ′} = v_MZ[1-(v²/c²)]^1/2/[1 - (vv_MY /c²)], (3.42) где v - модуль вектора v скорости движения (рис. 03.0.7) K′(x′, y′, z′, t′) подвижнаяИСО относительно K(x,y,z,t) неподвижнойИСО в положительном направления OYоси.

Выражения (3.40), (3. 41) и (3.42) представляют собой релятивистский закон сложения скоростей, если K′(x′, y′, z′, t′) подвижнаяИСО движется с вектором v скорости вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО.

С помощью(3.40), (3.41) получают проекции v_MX, v_MY, v_MZ вектора v_M скорости движения материальной M точки вK(x,y,z,t) неподвижнойИСО, если известны проекции v_{MX ′}, v_{MY ′}, v_{MZ ′} вектора v′_Mскорости движения той жематериальной M точки вK′(x′, y′, z′, t′) подвижнойИСО и известен модуль v вектора vскорости, с которойK′(x′, y′, z′, t′) подвижнаяИСО перемещается вдоль положительного направления OYоси K(x,y,z,t) неподвижнойИСО.

С помощью (3. 42) получают проекции v_{MX ′}, v_{MY ′}, v_{MZ ′} вектора v′_Mскорости движения материальной M точки вK′(x′, y′, z′, t′) подвижнойИСО, если известны проекции v_MX, v_MY, v_MZ вектора v_M скорости движения той жематериальной M точки вK(x,y,z,t) неподвижнойИСО и известен модуль v вектора vскорости, с которойK′(x′, y′, z′, t′) подвижнаяИСО перемещается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО.

Интервал между двумя событиями.

Интервалs′₁₂ или пространственно- временной интервал между двумя событиями, измеренный вK′(x′, y′, z′, t′) подвижнойИСО есть следующая величина: s′₁₂ = [с²(t′₁₂)² - (l′₁₂)²]^1/2, (3.43) где t′₁₂ = t′₂ - t′₁ - промежуток времени между рассматриваемыми событиями по часамвK′(x′, y′, z′, t′) подвижнойИСО, а l′₁₂ = [(x′₂ - x′₁)² + (y′₂ - y′₁)² + (z′₂ - z′₁)²]^1/2- расстояние между двумя точками, в которых совершаются события 1 и 2, измеренное также вK′(x′, y′, z′, t′) подвижнойИСО. Из частных преобразований Лоренца(3.11) следует, что (3.43) интервалмежду событиями 1 и 2 инвариантенпо отношению к выбору ИСО, т.е. не изменяется при переходе от K′(x′, y′, z′, t′) подвижнойИСО к K(x,y,z,t) неподвижнойИСО,поэтому имеет место следующее выражение: s′₁₂ = s₁₂, (3.44) где s₁₂ = [с²t₁₂² - l₁₂²]^1/2 - пространственно- временной интервалв K(x,y,z,t) неподвижнойИСО.Если s₁₂ - действительноечисло, то интервалназывается времени -подобным интервалом. Если s₁₂ - мнимоечисло, то интервал называется пространственно-подобным интервалом.

Элементы релятивистской динамики: основное уравнение релятивистской динамики

В релятивистскоймеханике, как и в ньютоновой (1.52) из раздела 01.0.0 "Физические основы механики", вектор p импульса материальной точки пропорционаленеё m массе и совпадает по направлению с вектором v скорости этой точки. Однако, в отличие от ньютоновоймеханики, вектор p импульса материальной точки является нелинейнойфункцией её вектора vскорости, поэтому имеет следующий вид: p = mv/[1 - (v²/c²)]^1/2. (3.45) В случае малостиv модуля вектора v скорости материальной точки m массой по сравнению со c скоростью света, т.е. v << c, выражение (3.45) совпадает с принятым в ньютоновоймеханике и имеет следующий вид: p = mv. (3.46) Под релятивистскимвектором F силы понимают по аналогии с ньютоновоймеханикой (1.42) из раздела 01.0.0 "Физические основы механики" первую производнуювектора p релятивистского(3.45) импульсапо t времени. Эта dp/dt первая производнаявектора p релятивистского импульсапо t времени, которая является нелинейнойфункцией от вектора vскорости и представляет собой основное уравнение релятивистской динамики, имеющее следующий вид: dp/dt = F или d{mv/[1 - (v²/c²)]^1/2}/dt = F. (3.47) Если на материальную точку одновременно действуют несколько сил, то под (3.47) вектором F силы (1.36) из раздела 01.0.0 "Физические основы механики" нужно понимать вектор равнодействующей силы.

Элементарная δAработавектораF_р равнодействующей силы на малом перемещении dr точки её приложения по аналогии с (1.80) из раздела 01.0.0 "Физические основы механики"имеет следующий вид: δA =F_рdr = F_рvdt. (3.48) С учетом (3.47) dp =Fdt и (3.45) p = mv/[1 - (v²/c²)]^1/2 выражение (3.48) элементарной δAработывектораF_р равнодействующей силы на малом перемещении dr точки её приложения к материальной точке m массой принимает следующий вид: δA = vdp = vdp = mvd{v/[1 - (v²/c²)] ^1/2} = = mv{v/[1 - (v²/c²)] ^1/2}′dv = mv/[1 - (v²/c²)] ^3/2dv = mc²{ v/c²[1 - (v²/c²)] ^3/2} dv =

= mc²d{1/[1 - (v²/c²)] ^1/2},(3.49)

где v - модуль вектора vскорости материальной точки m массой на её малом dr перемещении под действием приложенного вектораF равнодействующей силы; d{1/[1 - (v²/c²)] ^1/2} =

= {1/[1 - (v²/c²)] ^1/2}′ dv = { v/c²[1 - (v²/c²)] ^3/2} dv - дифференциал 1/[1 - (v²/c²)] ^1/2 в последнем равенстве (3.49) выражения.

Кинетическая энергия релятивистской частицы

Элементарное приращениеdW_kкинетической энергииматериальной точки по аналогии с (1.87) из раздела 01.0.0 "Физические основы механики" равно элементарной δAработевектораF силы на малом перемещении dr точки его приложения.

Кинетическая энергияW_k в произвольный момент t времени при достижении материальной точкой m массой модуля v вектора vскорости по теореме о кинетической энергии (1.87) из раздела 01.0.0 "Физические основы механики" с учётом (3.49) имеет следующий вид:

v

dW_k = δA = mc²d[1 - (v²/c²)] ^-1/2 ↔ W_k = mc² ∫ d[1 - (v²/c²)] ^-1/2 = mc²{[1 - (v²/c²)] ^-1/2 - 1}. (3.50)

0

С помощью разложения в выражении (3.50) [1 - (v²/c²)] ^-1/2 в ряд Маклоренаполучаемприближенное значение релятивистскоговыраженияW_k кинетической энергии материальной точки m массой и модулемv вектора vскорости, имеющее следующий вид:

W_k = mc²{ [(v²/c²)/2] + [3(v⁴/c⁴)/8] + …..}. (3.51)

Взаимосвязь м