Занятие 5. Колебания и волны

Задача 02.1.1, №13

Дано: r = 0,20 кг/с; χ₁ = 12 Н/м; χ₂ = 14 Н/м; m = 0,14 кг; l₁₀ = l₂₀= l₀ = 0,15 м; L = 0,14 м;v₀ = 0,10 м/с

------------------------------------------------------------------------------------------------------------------------------------

1) Дифференциальное уравнение свободных затухающих колебаний?

2) Угловая ω₀ частота и период T₀ гармонических колебаний?

3) Угловая ω частота и период T свободных затухающих колебаний?

4) Логарифмический δ декремент затухания?

5) Начальная A амплитуда и начальная φ₀ фаза свободных затухающих колебаний?

6)Ууравнение свободных затухающих гармонических колебаний?

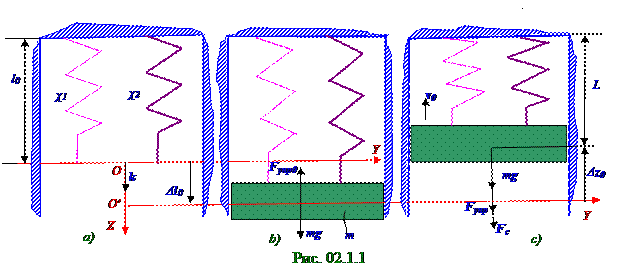
При статическомрастяжении (рис. 02.1.1,b) на длину l₀ двух соединённых параллельно пружин c χ₁, χ₂ жёсткостямипод действием груза массой m эквивалентнаяχ_экв жёсткостьопределяется из следующего выражения: χ_экв = χ₁ + χ₂ = 26 Н/м.(1.1) Согласно (2.2) из раздела 02.0.0 "Колебания и волны" дифференциальному уравнению гармоническихколебаний циклическая ω₀ частота и периодT₀ этих гармонических колебаний, т.е. в отсутствие потерь энергии, когда β = 0, имеет следующее значение: ω₀ = (χ_экв /m)^1/2 ≈ 13,60 рад/с; T₀ = 2π/ω₀ ≈ 0, 46 с.(1.2)Согласно (2.47) из раздела 02.0.0 "Колебания и волны" дифференциальному уравнению свободных затухающихколебаний (d²z/dt² ) + 2β(dz/dt ) + zω₀ ² = 0 и решению (2.48) из раздела 02.0.0 "Колебания и волны" этого дифференциального уравнения периодT и циклическаяωчастота свободных затухающихколебаний с учётом (1.2) имеет следующее значение:

T = 2π/ω =2π/(ω₀ ²- β²)^{1/ 2} ≈ 0, 46 с; ω = 2π/T ≈ 13,60 рад/с,(1.3) где β = r/2m ≈ 0,71 1/с - коэффициент затухания. В силу небольшой величины коэффициента

β затухания он незначительно влияет на периодT и циклическуюωчастоту свободных затухающихколебаний.

Согласно (2.52) из раздела 02.0.0 "Колебания и волны" логарифмический δдекремент затуханияс учётом (1.3) имеет следующее значение: δ = βT ≈ 0,33. (1.4) Число N свободных затухающихколебаний, в течение которых амплитуда уменьшается в e раз с учётом (1.4), имеет следующее значение: N = 1/δ ≈ 3.(1.5) Согласно (2.49) из раздела 02.0.0 "Колебания и волны" постоянные величины A₀ и φ₀ соответственно начальная амплитуда и начальная фазаколебаний определяются в начальный момент t₀ времени, т.е. при t₀ = 0, и имеют согласно z = A₀e^{- βt}cos(ωt + φ₀) решению (2.47) из раздела 02.0.0 "Колебания и волны" дифференциального уравнения свободных затухающих гармоническихколебанийследующий вид:

z₀|_t0=0 = A₀e^{- βt}cos(ωt + φ₀)| _t0=0 ↔ z₀ = A₀cosφ₀ ↔ A₀ = z₀/cosφ₀ (1.6) v_0Z|_t0=0 = (dz/dt)|_t0=0 = d[A₀e^{- βt}cos(ωt + φ₀)]/dt|_t0=0

= [-A₀βe^{- βt}cos(ωt + φ₀) - A₀ωe^{- βt}sin(ωt + φ₀)]|_t0=0 ↔ v_0Z =- A₀(βcosφ₀ + ωsinφ₀).(1.7) Подставляем (1.6) A₀начальную амплитудув(1.7) v_0Z проекцию на OZ ось вектора

v₀ начальнойскорости иполучаемследующее значение φ₀ начальной фазысвободных затухающих гармоническихколебаний шайбы m массой:

v_0Z = - (z₀/cosφ₀)(βcosφ₀ + ωsinφ₀) ↔ tgφ₀ = - (v_0Z + βz₀)/ωz₀ ≈ - 0,17; φ₀ ≈ 170^º, (1.8) где (рис. 02.1.1,c) z₀ = L - l₀ - Δl₀ = 0, 14 - 0, 15 - 0, 053 = -0,063 м - начальное смещение относительно начала O′ координат, совмещённого с положением шайбы m массой в статическомсостоянии, т.е. при растяжения пружинышайбой массы m без возникновенияколебаний, определяется разностью заданной в условии L длины пружиныс шайбой массы mв деформированномсостоянии в начальный t₀ = 0 момент времени и (рис. 02.1.1,a) длины l₀пружиныв недеформированномсостоянии с учётом Δl₀ = mg/χ_экв≈ 0, 053 мстатическогорастяжения пружины из (2.1) из раздела 02.0.0 "Колебания и волны" под воздействием mg силы тяжести шайбы; v_0Z - проекция вектора v₀ начальнойскорости на OZ ось груза m массой, которая имеет в (1.8) отрицательное значение, поскольку этот вектор v₀ начальнойскорости противоположен по направлению OZ оси; β = 0, 71 1/с - коэффициент (1.3) затухания свободныхколебаний шайбы m массой; ω≈ 13,60 рад/с - циклическая(1.3) частота свободных затухающихколебаний шайбы m массой.

Подставляем значение начальной φ₀ = 170^º фазы свободных затухающихколебаний из (1.8) в выражение (1.6) и получаем следующее значение начальнойA амплитуды этих свободных затухающихколебаний груза m массой: A₀ = z₀/cosφ₀ ≈ 0, 064 м.(1.9) Уравнение свободных затухающихколебаний с учётом их циклической(1.3) ω ≈ 13,6 рад/счастоты, коэффициента β ≈ 0,71 1/сзатухания, начальной(1.7) φ₀≈ 2, 97 рад фазыи начальной

A₀ = 0, 064 мамплитудыэтих свободных затухающихколебаний имеет следующий вид:

z ≈ 0, 064e^-0,71tcos(13,60t + 2, 97) м.(1.10)

Моделирование задачи в программной среде "Живая физика" подтверждает правильность решения этой задачи.

Задача 02.1.2 №24

6) Уравнение свободных затухающих колебаний?

Статическое l₀ смещение (рис. 02.1.2) относительно 0 координат, т.е. поверхности жидкости, из условия равновесия пробирки с дробью до возникновения колебаний определяется из следующей проекции на OZ осьвторогозакона Ньютонапри условии равенства нулю ускорения:

OZ: 0 = mg - ρSl₀g ↔ mg = ρSl₀g ↔ l₀ = m/ρS =0,10 м,(2.1)

где F_А0 =ρSl₀g – проекция на OZ осьвектора F_А0 силы Архимедапри статическом l₀ смещениипробирки с дробью m массой; ρ – плотность жидкости, в которой находится пробирка с дробью;

S – площадь поперечного сечения этой пробирки.

Начальное z₀ смещение относительно начала O′ координат, совмещённого с положением пробирки с дробью при статическом l₀ смещение относительно 0 координат, т.е. поверхности жидкости, с учётом (2.1) имеет следующее значение: z₀ = H - l₀ = 1, 2l₀ - l₀ = 0,02 м,(2.2)

где H - расстояние от дна пробирки с дробью до поверхности жидкости при её выведении из состояния статического равновесия; z₀ - начальное (рис. 02.1.2) смещение имеет положительное значение потому, что в начальный момент t₀ времени, т.е. при t₀ = 0, пробирка с дробью была заглублена относительно статического l₀ смещения на это z₀ начальное смещение.

Согласно (2.47) из раздела 02.0.0 "Колебания и волны" дифференциальное уравнение свободных затухающихколебаний по OZ оси пробирки с дробью m массой, имеющее в произвольный t момент времени z смещение (рис. 02.1.2) и скорость v = dz/dt относительно начала O′ координатс учётом (2.1) имеет следующий вид: OZ: m(d²z/dt² ) = mg - F_АZ+ F_Zc ↔ m(d²z/dt² ) =

= mg - ρSg(l₀ + z) + r(dz/dt )cos(v,^k) ↔ m(d²z/dt² ) = - ρSgz - r(dz/dt ) ↔

↔ md²z/dt² + r(dz/dt ) + ρSgz = 0 ↔ (d²z/dt² ) + 2β(dz/dt ) +(ρSg/m)z = 0, (2.3)

где β = r/2m > 0 - коэффициент затухания, а ω₀ = (ρSg/m)^1/2 - циклическая частота свободных незатухающих гармонических колебаний пробирки с дробью, т.е. в отсутствие потерь энергии, когда β = 0; F_АZ =- ρSg(l₀ + z) - проекция (рис. 02.1.2) на OZ осьвектора F_А силы Архимедаприсмещении пробирки с дробью m массой относительно её статического l₀ смещения на z величину;

F_Zc = r(dz/dt ) cos(v,^k) = - r(dz/dt ) - проекция (рис. 02.1.2) на OZ осьвектора F_c силы сопротивления, который направлен в сторону OZ оси, т.е. коллинеарен k единичному векторуи направлен с ним в одну и ту же сторону, т.е. направлен противоположно вектору v₀ начальнойскорости, поэтому

cos(v,^k) = - 1.

Циклическая (2.47) из раздела 02.0.0 "Колебания и волны" ω₀ частота и периодT₀ свободных незатухающихколебаний пробирки с дробью, т.е. в отсутствие потерь энергии, когда β = 0, имеет следующее значение: ω₀ = (ρSg/m)^1/2 ≈ 9, 90 рад/с; T₀ = 2π/ω₀ ≈ 0, 63 с.(2.4) Согласно (2.47) из раздела 02.0.0 "Колебания и волны" дифференциального уравнения свободных затухающихколебаний (d²z/dt² ) + 2β(dz/dt ) + ω₀ ²z² = 0 и решения (2.48) из раздела 02.0.0 "Колебания и волны" этого дифференциального уравнения T периоди циклическаяωчастота свободных затухающихколебаний пробирки с дробью с учётом (2.4) имеет следующее значение: T = 2π/ω =2π/(ω₀ ²- β²)^{1/ 2} ≈ 0, 63 с; ω = 2π/T ≈ 9, 90 рад/с,(2.5) где β = r/2m = 0, 50 1/с - коэффициент затухания. В силу небольшой величины коэффициента

β затухания он незначительно влияет на T периоди циклическуюωчастоту свободных затухающихколебаний.

Согласно (2.52) из раздела 02.0.0 "Колебания и волны" логарифмический δдекремент затухания свободныхколебаний с учётом (2.5) имеет следующее значение: δ = βT ≈ 1, 00.(2.6) Число N свободных затухающихколебаний, в течение которых амплитуда уменьшается в e раз с учётом (2.6), имеет следующее значение: N = 1/δ ≈ 1.(2.7)

Согласно (2.49) из раздела 02.0.0 "Колебания и волны" постоянные величины A₀ и φ₀ соответственно начальная амплитуда и начальная фазаопределяются в начальный момент t₀ времени, т.е. при t₀ = 0, и имеют согласно z = A₀e^{- βt}cos(ωt + φ₀) решению (2.47) из раздела 02.0 "Колебания и волны" дифференциального уравнения свободных затухающихколебанийследующий вид: z₀|_t0=0 = A₀e^{- βt}cos(ωt + φ₀)| _t0=0 ↔ z₀ = A₀cosφ₀ ↔ A₀ = z₀/cosφ₀ (2.8) v_0Z|_t0=0 = (dz/dt)|_t0=0 = d[A₀e^{- βt}cos(ωt + φ₀)]/dt|_t0=0

= [-A₀βe^{- βt}cos(ωt + φ₀) - A₀ωe^{- βt}sin(ωt + φ₀)]|_t0=0 ↔ v_0Z =- A₀(βcosφ₀ + ωsinφ₀).(2.9) Подставляем (2.8) Aначальную амплитудув(2.9) v_0Z проекцию на OZ ось вектора

v₀ начальнойскорости иполучаемследующее значение φ₀ начальной фазысвободных затухающихколебаний пробирки с дробью m массой:

v_0Z = - (z₀/cosφ₀)(βcosφ₀ + ωsinφ₀) ↔ tgφ₀ = - (v_0Z + βz₀)/ωz₀ ≈ 0,15; φ₀ ≈ 2^º 50', (2.10) где (рис. 02.1.2) z₀ = 0,02 м - начальное (2.2) смещение относительно начала O′ координат, совмещённого с положением пробирки с дробью m массой в статическомсостоянии, т.е. относительно положения пробирка с дробью, погружённой под воздействием mg силы тяжести в жидкость на длину статического l₀ смещения; v_0Z = - 0,02 м/с - проекция вектора v₀ начальнойскорости на OZ ось пробирки с дробью m массой, которая имеет в (2.10) отрицательное значение, поскольку этот вектор v₀ начальнойскорости противоположен по направлению OZ оси; β = 0, 50 1/с - коэффициент (2.5) затухания свободных гармонических колебаний пробирки с дробью m массой; ω≈ 9, 90 рад/с- циклическая частота свободных затухающихколебаний пробирки с дробью m массой. Подставляем значение начальной φ₀ = 2^º 50' фазы свободных затухающихколебаний из (2.10) в выражение (2.8) и получаем следующее значение начальнойA₀ амплитуды этих свободных затухающихколебаний: A₀ = z₀/cosφ₀ ≈ 0, 02 м. (2.11) Уравнение свободных затухающихколебаний с учётом их циклической(2.5) ωчастоты, коэффициента β затухания, начальной(2.10) φ₀≈ 0, 05 рад фазыи начальнойA₀ = 0, 02 мамплитудыэтих свободных затухающихколебаний имеет следующий вид: z ≈ 0, 02 e^-0,5tcos(9, 90t + 0, 05) м.(2.12)

Задача 02.1.3 №28

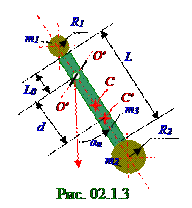
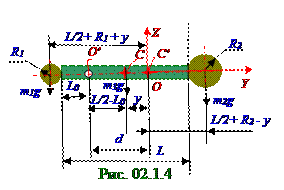
(рис.2.12) из раздела 02.0.0 "Колебания и волны" до O′O′ оси его вращения, вследствие чего (рис. 02.1.4) для y_{C '} координаты C′ центра масс этого ФМ имеет место следующее выражение:

y_{C '} = [-m₃y + m₂ (L/2+ R₂ - y) - m₁(L/2+ R₁ + y)]/(m₁ + m₂ + m₃),(3.1)

Начало O координат (рис. 02.1.4) совмещено с C′ центром масс ФМ, поэтому в этой OYZ системе y_{C '} координата C′ центра масс этого ФМ равна нулю, т.е. y_{C '} = 0, и выражение (3.1) принимает следующий вид:

0 = -m₃y + m₂ (L/2+ R₂- y) - m₁(L/2+ R₁ + y) ↔ y ≈ 0, 11 м ↔ d = L/2- L₀ + y ≈ 0, 26 м, (3.2)где y-расстояние (рис. 02.1.4) между C′ центром масс ФМ и C центром масс стержня Lдлиной.

имеет следующий вид: d²α/dt² +( mgd/J_O'O')α = 0. (3.4) Решение (3.4) дифференциального уравнение гармонических колебанийФМ относительно O′O′ оси вращения (2.43) из раздела 02.0.0 "Колебания и волны" имеет следующий вид: α = α₀cos(ω₀t + φ₀), (3.5) где α₀ и φ₀ - соответственно амплитуда и начальная фаза колебанийгармонических малых колебаний физического маятника.

Циклическая ω₀ частота и T₀ период гармонических колебаний ФМ с учётом (2.44) из раздела 02.0 "Колебания и волны", а также с учётом (3.2) расстояния d от C′ центра масс ФМ до O′O′ осивращения,(3.3) момента J _O'O'инерции ФМ относительно этой O′O′ оси вращения и

общей m = m₁ + m₂+ m₃ массы ФМ имеет следующее значение:

ω₀ = [(mgd)/J_O'O']^1/2 ≈ 6,80 c^-1 и T₀ = 2π/ω₀ ≈ 0, 92 c. (3.6) Согласно (2.49) из раздела 02.0.0 "Колебания и волны" постоянные величины α₀ и φ₀ соответственно амплитудаиначальная фазаколебаний определяются (3.5) из начальных условий при

t₀ = 0 с учётом начального α_н = 45º угла отклонения ФМ от положения равновесия, а также с учётом согласно условию равенства нулюзначения ω_н= (dα/dt)|_t0=0 = 0 начальной угловой скорости этого ФМ, вследствие чего для определения постоянных величин α₀ и φ₀ соответственноамплитудыиначальной фазыколебаний ФМ имеют место следующие выражения:

α|_t0=0 = α₀cos(ω₀t + φ₀)|_t0=0 = α_н ↔ α_н = α₀cosφ₀ ↔ α₀ = α_н/cosφ₀; (3.7) ω₀ |_t0=0 = ω_н= (dα/dt) |_t0=0 = dα₀cos(ω₀t + φ₀)/dt |_t0=0 = - α₀ω₀sin(ω₀t + φ₀) |_t0=0 ↔

↔ ω_н= - α₀ω₀sinφ₀ ↔ 0 = - α₀ω₀sinφ₀ ↔φ₀ = 0 рад.(3.8)Подставляем (3.8) значение φ₀ = 0 радначальной фазы гармонических колебаний ФМ в (3.7) и получаем следующее значение α₀ амплитуды колебаний этого ФМ: α₀ = α_н = 45º = 0, 78 рад. (3.9) Уравнение гармоническихколебаний ФМ с учётом их циклической(3.6) ω₀≈ 6,8 c^-1 частоты, начальной(3.7) φ₀= 0 рад фазыи α₀ = 45º = 0, 78 рад амплитудыимеет следующий вид:

α ≈ 0, 78cos6, 80t рад. (3.10)