Вероятностный автомат объекта.
Одним из наиболее эффективных инструментов моделирования сложных стохастических систем является методология вероятностно-автоматного моделирования.
Эффективность названной методологии обусловливают следующие две ее особенности:
1) наличие средств, обеспечивающих адекватное описание сложных стохастических систем и процессов их функционирования;
2) возможность построения унифицированных моделей для широкого класса систем.
Основополагающим понятием методологии является понятие вероятностного автомата как некоторого объекта, обладающего внутренним состоянием, способного воспринимать входной сигнал и выдавать выходной. В соответствии с этим состояние вероятностного автомата в каждый момент времени полностью характеризуется тремя величинами: внутренним состоянием, входным сигналом и выходным сигналом. Каждая из этих величин может быть либо скалярной, либо векторной. Отсюда следует, что описание вероятностного автомата может быть представлено:
1) внутренним алфавитом, т.е. множеством допустимых значений внутреннего состояния;
2) входным алфавитом, т.е. множеством всех возможных значений входного сигнала;
3) выходным алфавитом, т.е. множеством всех возможных значений выходного сигнала.
Кроме того, для полной определенности функционирования автомата необходимо задать еще начальное состояние автомата и правила, на основании которых происходит выбор выходного сигнала.
Дополнительно условимся, что автомат является дискретным, т.е. поступление входных сигналов, изменение внутреннего состояния и формирование выходных сигналов происходят лишь в целочисленные моменты времени. Автомат, удовлетворяющий всей совокупности перечисленных условий, в специальной литературе получил название автомата Мура. Таким образом, рассматриваемый здесь автомат может быть однозначно задан совокупностью шести объектов:
X, А, У, а„ А(х), 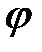 (а),
(а),
где X, А, У- соответственно входной, внутренний и выходной алфавиты автомата;
а0(а0 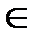 А) - начальное состояние автомата;
А) - начальное состояние автомата;
А(х)(х 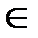 X) - семейство стохастических матриц, определяющих правила перехода автомата из одного состояния в другое;
X) - семейство стохастических матриц, определяющих правила перехода автомата из одного состояния в другое;
 (а)(а
(а)(а 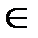 A,
A,  ) -функция выходов автомата.
) -функция выходов автомата.
Функционирование автомата происходит следующим образом. В каждый из дискретных моментов времени на вход автомата поступает входной сигнал из множества сигналов входного алфавита. Под воздействием поступившего сигнала происходит изменение внутреннего состояния автомата (в рамках множества состояний, определяемых внутренним алфавитом), и формируется выходной сигнал из множества сигналов выходного алфавита. Преобразование внутреннего состояния автомата осуществляется в соответствии с семейством стохастических матриц А(х). Число матриц в этом семействе должно соответствовать числу символов входного алфавита, а размерность - числу внутренних состояний автомата (т.е. числу символов в его внутреннем алфавите), причем элементами каждой из этих матриц должны быть значения Р 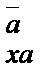 - вероятности того, что если автомат находился в состоянии
- вероятности того, что если автомат находился в состоянии 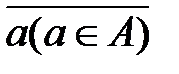 , то при поступлении сигнала х(х
, то при поступлении сигнала х(х 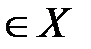 ) автомат перейдет в состояние а(а
) автомат перейдет в состояние а(а 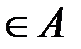 ). Формирование выходного сигнала осуществляется в соответствии с функцией выходов
). Формирование выходного сигнала осуществляется в соответствии с функцией выходов  (а), которая может быть как детерминированной, так и стохастической. Если данная функция является детерминированной, то в ней должен быть определен выходной сигнал для каждой пары возможных переходов внутреннего состояния автомата, т.е. значение Y(ai
(а), которая может быть как детерминированной, так и стохастической. Если данная функция является детерминированной, то в ней должен быть определен выходной сигнал для каждой пары возможных переходов внутреннего состояния автомата, т.е. значение Y(ai  аj); y
аj); y 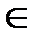 Y, ai
Y, ai 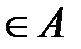

Если же функция 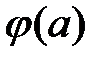 является стохастической, то для каждого потенциально возможного перехода аi
является стохастической, то для каждого потенциально возможного перехода аi 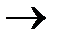 aj должен быть задан вектор
aj должен быть задан вектор  , где Py есть вероятность того, что при данном переходе выходной сигнал примет значение у (у
, где Py есть вероятность того, что при данном переходе выходной сигнал примет значение у (у 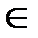 Y).
Y).
Нетрудно видеть, что перечисленные правила позволяют достаточно адекватно описать весьма широкий круг объектов реальных систем. Однако, как показала практика, семейство матриц А (х) часто оказывается громоздким, что затрудняет их применение, но почти во всех случаях семейство матриц можно существенно упростить, если учесть особенности функционирования конкретных объектов. Объективной предпосылкой такого упрощения служит то обстоятельство, что во многих реальных объектах различные условия (сочетания входных сигналов и текущих внутренних состояний) приводят к переходу автомата в одно и то же состояние (или к одному и тому же распределению вероятностей перехода). На основе объединения указанных совпадений формируется так называемая таблица условных функционалов переходов (ТУФП), представляющая собою таблицу, в верхней строке которой приведены варианты условий, приводящих к тем или иным переходам, а в нижней - сами переходы (или распределение вероятностей переходов) для соответствующих условий.
Так в общих чертах могут быть представлены принципы вероятностно-автоматного моделирования процессов функционирования отдельно взятого объекта. Однако в подавляющем большинстве практических приложений изучаются большие системы, состоящие из некоторой совокупности взаимосвязанных объектов. С помощью рассмотренных выше методов могут быть построены вероятностно-автоматные модели каждого из объектов системы. Объединение автоматов в систему будет заключаться в отождествлении выходных сигналов одних автоматов с входными сигналами других. Само собою разумеется, отождествление должно осуществляться в строгом соответствии с взаимосвязями реальных объектов моделируемой системы, причем выходные и входные алфавиты сопрягаемых автоматов должны быть согласованными в том смысле, что входной алфавит принимающего автомата должен содержать все символы выходного алфавита передающего автомата.
Описание связей между автоматами может быть осуществлено с помощью графа межавтоматных связей: структура системы изображается в виде направленного графа, между вершинами которого и автоматами, моделирующими элементы системы, установлено взаимно однозначное соответствие. Если состояние какого-то одного автомата участвует в формировании состояния другого, то на графе межавтоматных связей это изображается направленной дугой от первого к второму. Описание структуры системы автоматов указанным способом является достаточно наглядным. Однако если количество автоматов, образующих систему, велико, то графическое описание межавтоматных связей становится громоздким и неудобным для использования. В таких случаях предпочтительней будет матричное описание структуры системы: строится квадратная матрица, порядок которой совпадает с числом автоматов системы, а элементы принимают значения 1 или 0 в зависимости от того, есть связь от автомата, номер которого совпадает с номером строки матрицы, к автомату, номер которого совпадает с номером столбца матрицы, или такой связи нет.
Матрицу связей автоматов можно сделать более информативной, если в качестве ее элементов принять не просто 0 и 1, информирующие лишь о наличии или отсутствии связи, а символы, содержащие информацию также о характере связей, например: Д - двоичная связь (в выходном алфавите соответствующего автомата содержатся лишь два символа), Т - троичный, Н - натуральный (множество всех натуральных целых чисел) и т.п.
Для организации моделирования дополнительно необходимо задать начальные состояния всех автоматов и перечень тех автоматов, выходные сигналы которых должны фиксироваться в качестве результатов моделирования.
Так в самых общих чертах могут быть представлены основные положения методологии вероятностно-автоматного моделирования. Более детально изучить ее можно, прочитав[21].
В гл. 3 будет приведен конкретный пример использования методов вероятностно-автоматного моделирования для решения задач защиты информации.
Нетрудно видеть, что статистическое моделирование отличается достаточно высокой степенью общности. Это создает предпосылки для построения унифицированной модели, легко адаптируемой к широкому классу задач зашиты информации.
Рассмотрим возможности и пути построения такой модели. Все имитационные модели удобно классифицировать по следующим трем
показателям: 1) участие человека в подготовке модели к работе; 2) участие человека непосредственно в процессе работы модели; 3) стабильность модели в процессе функционирования.
По первому показателю модели могут быть разделены на необучаемые и обучаемые. К необучаемым относятся такие модели, у которых механизм поиска решения полностью формируется на этапе их разработки. Иными словами, необучаемые модели готовы к выполнению своих функций сразу после их разработки и отладки. К обучаемым относятся модели, у которых механизм поиска решения нуждается в настройке (обучении) с помощью экспертов. Акт обучения может быть одноразовым (перед включением модели в конкретную систему с целью решения задач определенного класса) и периодическим.
По второму показателю модели можно разделить на пассивные и активные. В пассивных моделях поиск решения осуществляется без непосредственного участия человека; в активных моделях человек принимает непосредственное участие в технологическом процессе поиска решения. Иными словами, в активных моделях процесс поиска решений осуществляется в интерактивном режиме.
В зависимости от сочетания значений рассмотренных показателей классификационная структура имитационных моделей будет такой, как показано на рис. 4.6.
По стабильности структуры имитационные модели делятся на немодифицируемые и модифицируемые. В общем случае модели каждого из выделенных на рис. 4.6 типов могут быть как немодифицируемыми, так и модифицируемыми. Тогда общую классификацию и идентификацию имитационных моделей можно представить так, как показано в табл. 4.2. В соответствии с рассмотренной классификацией обобщенная структура имитационной модели представлена на рис. 4.7. Выделенные ни рис. 4.7 блоки в каждом из типов моделей будут использоваться в различном сочетании. Сочетание этих блоков для различных типов моделей показано в табл. 4.3.
На основе этих данных можно построить так называемую структурную формулу модели, состоящую из последовательности нулей и единиц, причем номера позиций, значения которых равны 1, соответствуют номерам блоков обобщенной схемы, используемых в модели соответствующего типа. Если же значение позиции равно 0, то соответствующий блок в модели не используется. Структурные формулы моделей приведены к правом столбце табл. 4.3. Они предназначены для организации управления процессом формирования структур моделей при моделировании конкретных систем.
Рис. 4.6. Классификация имитационных моделей по степени участия
Человека
Таблица 4.2. Общая классификация и идентификация имитационных моделей
| Идентификатор | Название |
| НПН-модели | Необучаемые пассивные немодифицируемые |
| НПМ-модепи | Необучаемые пассивные модифицируемые |
| ОПН-модели | Обучаемые пассивные немодифицируемые |
| ОПМ-модеяи | Обучаемые пассивные модифицируемые |
| НАН-модели | Необучаемые активные немодифицируемые |
| НАМ-модеяи | Необучаемые активные модифицируемые |
| ОАН-модели | Обучаемые активные немодифицируемые |
| ОАМ-модели | Обучаемые активные модифицируемые |
Рис. 4.7. Обобщенная структура имитационной модели
Таблица 4.3. Использование блоков обобщенной схемы в моделях различных типов
| Идентификатор модели | Использование в модели блоков обобщенной схемы | Структурная формула модели | ||||||
| НПН-модели | — | + | — | — | + | + | ||
| НПМ-модели | — | + | + | — | + | + | ||
| ОПН-модели | + | + | __ | __ | + | + | ||
| ОПМ-модели | + | + | + | — | + | + | ||
| НАН-модели | — | + | __ | + | + | + | ||
| НАМ-модеяи | __ | + | + | + | + | + | ||
| ОАН-модели | + | + | __ | + | + | + | ||
| ОАМ-модели | + | + | + | + | + | + | ||
Примеры применения имитационных моделей для решения конкретных задач, связанных с созданием и использованием систем защиты информации, будут приведены при рассмотрении соответствующих вопросов.
Дата добавления: 2016-03-15; просмотров: 1131;
