Замечание о симметрии тела
Пусть тело имеет плоскость симметрии, которую совмещаем с плоскостью Oxy (рис. 65). Ввиду симметрии каждому элементу тела vk с координатой zk (расположенному над плоскостью симметрии) соответствует такой же элемент vk с координатой zk, который расположен под плоскостью симметрии. В этом случае в выражениях (4.8) координата
.
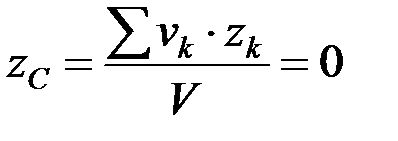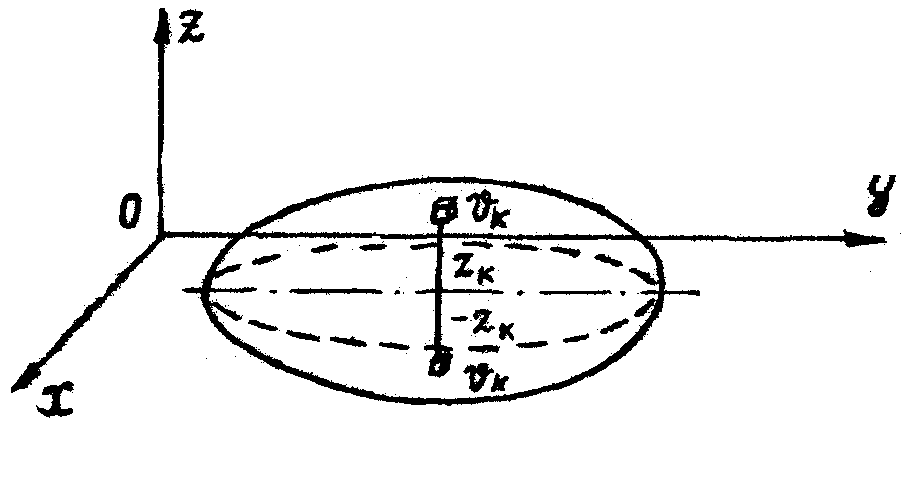
| Рис. 65 |
1. Если тело имеет плоскость симметрии, его центр тяжести находится в этой плоскости.
2. Если тело имеет две плоскости симметрии, его центр тяжести находится на линии их пересечения.
3. Если тело имеет три плоскости симметрии, его центр тяжести находится в точке их пересечения.
Рассмотрим примеры определения координат центров тяжести некоторых однородных тел.
Пример 1
| Рис. 66 |
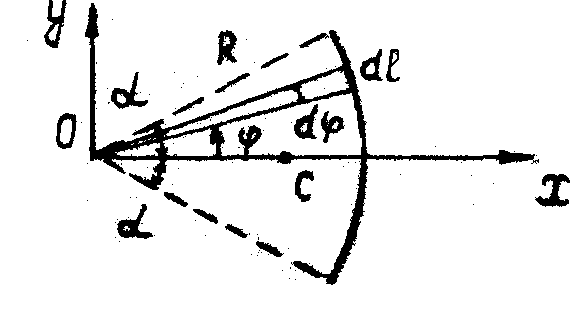Центр тяжести однородной дуги радиусом R и центральным углом 2a.
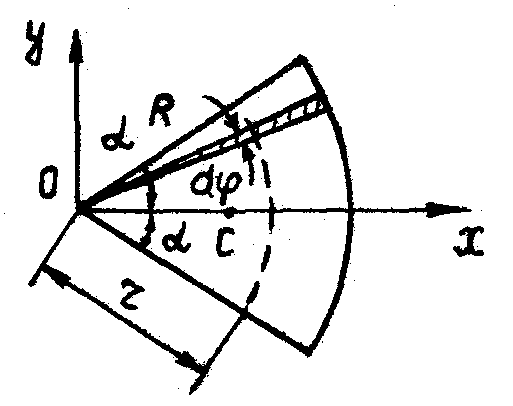
Совмещаем ось Ох (рис. 66) с осью симметрии дуги АВ. Тогда координата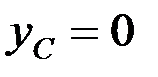 
. Для определе-ния координаты 
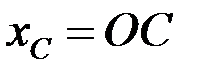воспользуемся выражением из формулы (4.14)
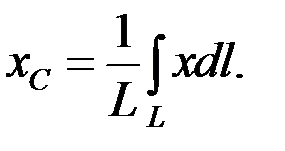(4.16)
Выделяем на центральном угле j бесконечно малую дугу dl с центральным углом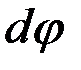 
. Тогда
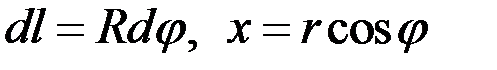и длина дуги 
.
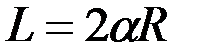Подставляя эти значения в выражение (4.15), получаем:
.
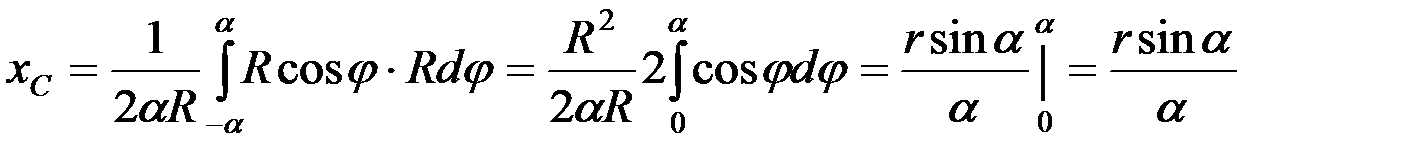Следовательно, координата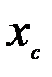 
центра тяжести однородной дуги определяется выражением
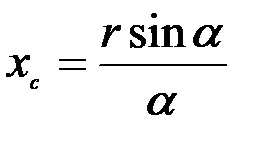, (4.16)
где a – половина центрального угла дуги в радианах.
Пример 2
Центр тяжести треугольника.
Разбиваем треугольник (рис. 67) на бесконечно тонкие полоски, параллельные стороне АД. Так как полоски имеют бесконечно малую ширину, можно считать, что их центры тяжести находятся на середине длинных сторон полосок. Следовательно, центры тяжести таких полосок находятся на меридиане ВК.
| Рис. 67 |
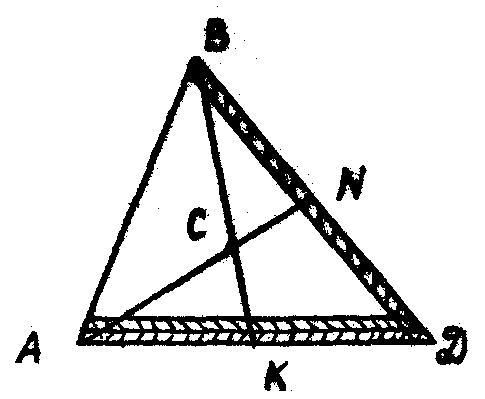Разбивая треугольник на тонкие полоски параллельные стороне ВД, получим, что их центры тяжести лежат на медиане AN. Следовательно, центр тяжести треугольника C находится в точке пересечения его медиан.
При этом очевидны соотношения:
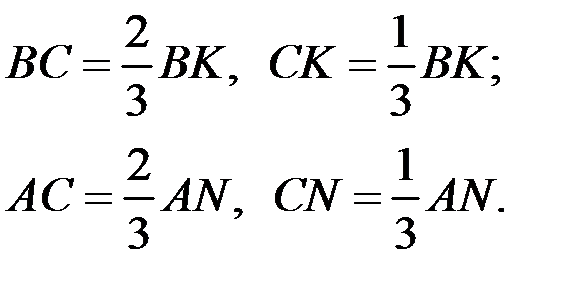
Пример 3
Центр тяжести однородного сектора с центральным углом 2a и радиусом R.
| Рис. 68 |
.
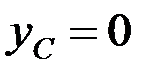Выделяем из сектора элементар-ный сектор с бесконечно малым углом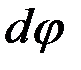 
. Этот элементарный сектор можно считать треугольником, центр тяжести которого находится на расстоянии 
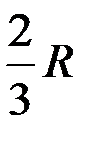, поэтому центры тяжести элементарных секторов находятся на дуге 
.
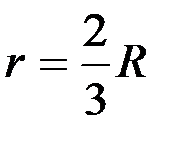Используя выражение (4.16) для центра тяжести дуги, получаем координаты центра тяжести однородного сектора:
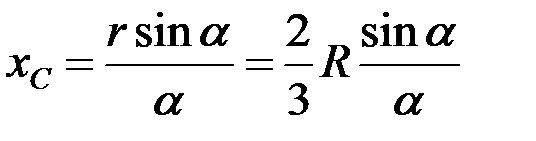. (4.17)
В выражении (4.17) α – половина центрального угла сектора, выражается в радианах.
Пример 4
Определить координаты центра тяжести однородного плоского тела (рис. 69), которое получается, если из квадрата 1 со стороны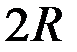 
вырезана четвёртая часть круга 2 радиусом R и присоединён треугольник 3.
Задачу решаем методом отрицательных площадей.
| Рис. 69 |
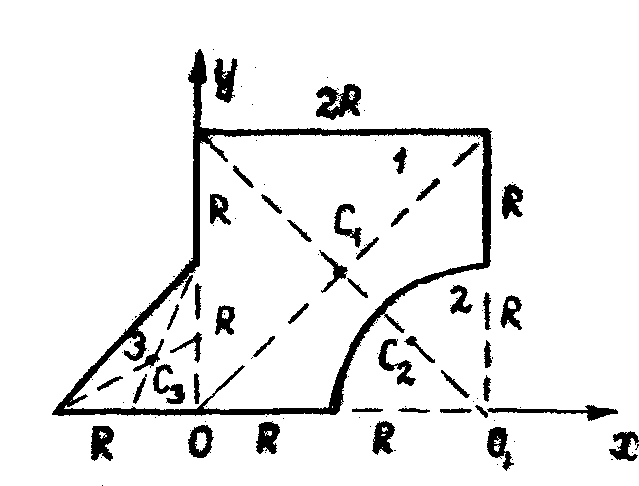Разбиваем тело на три элемента. Определяем площадь и координаты центров тяжести каждого элемента.
1. Квадрат без выреза
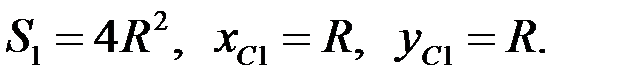
2. Четверть круга с отрицательной площадью
| – |
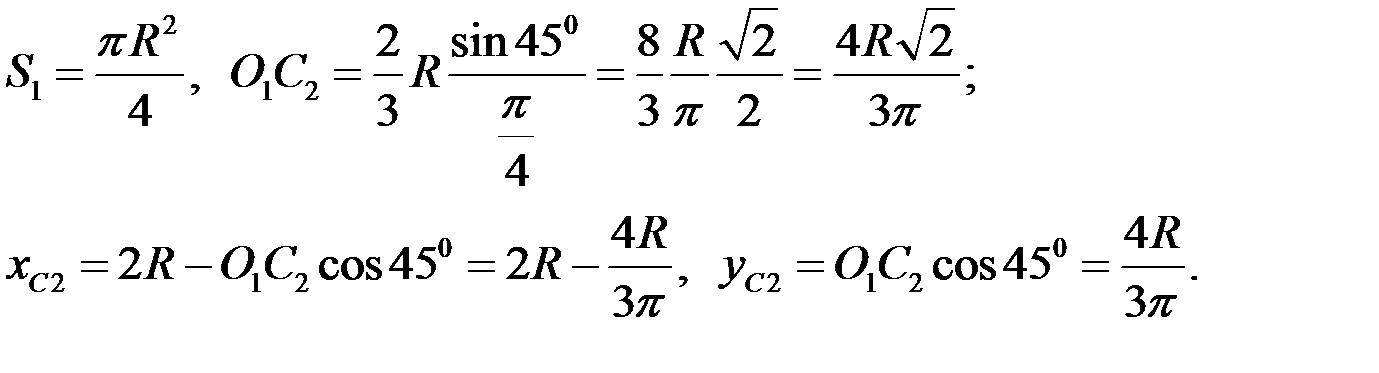
3. Треугольник
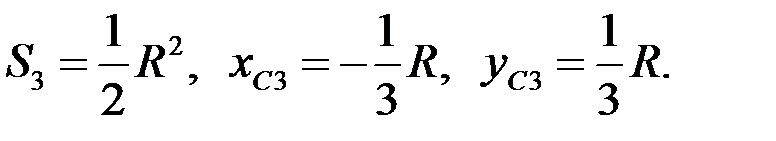
Находим координаты центра тяжести тела
;
.
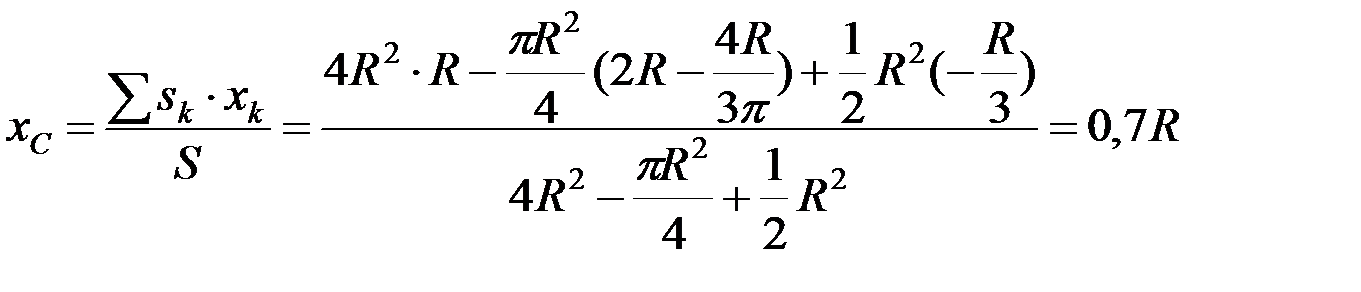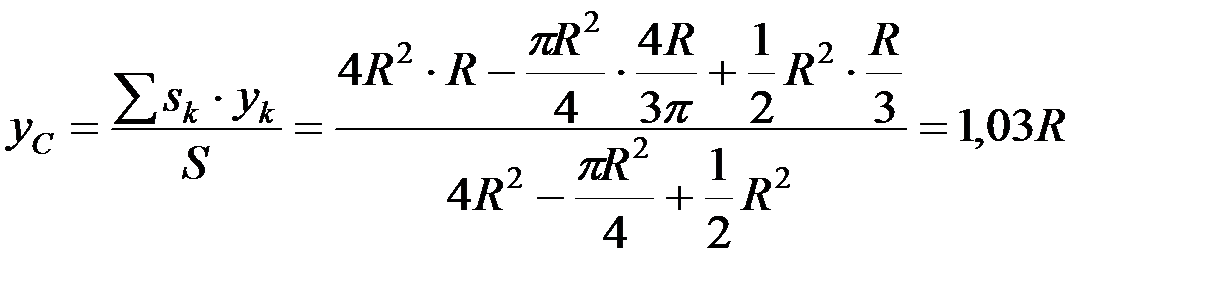КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется центром параллельных сил? Каково его основное свойство?
2. По каким формулам вычисляются координаты центра параллельных сил?
3. Что называется центром тяжести тела?
4. Как определяются координаты центра тяжести тела в общем случае?
5. По каким формулам вычисляются координаты центров тяжести однородных объёмных тел, плоских фигур и линий?
6. Что называется статическим моментом площади плоской фигуры относительно оси? Как он вычисляется? Какую размерность имеет?
7. В чём сущность метода отрицательных площадей при определении координат центров тяжести плоских тел?
Дата добавления: 2016-03-15; просмотров: 765;