Центр параллельных сил
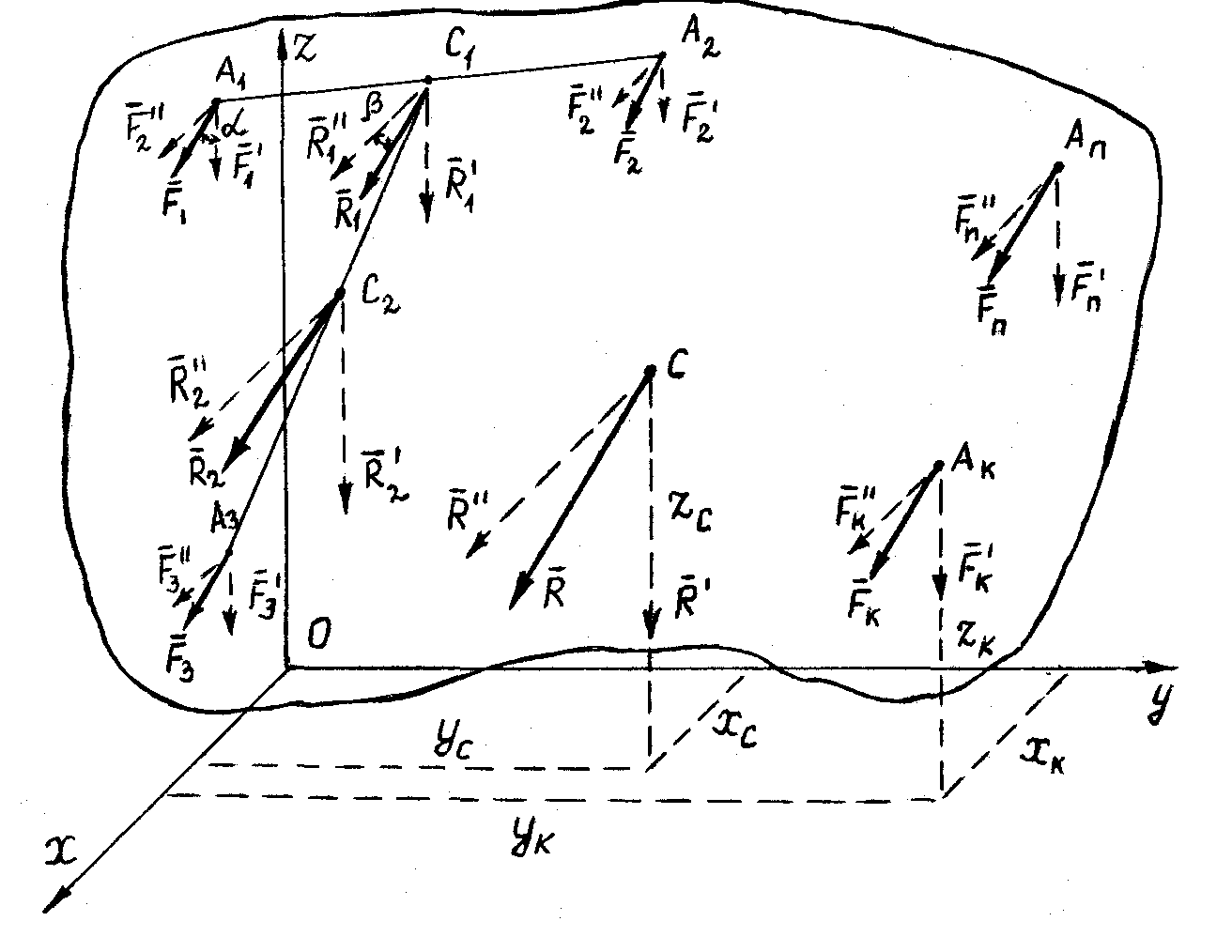
| Рис. 63 |
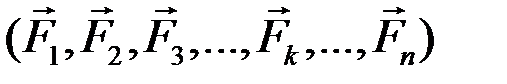 (рис. 63). Силы приложены в точках
(рис. 63). Силы приложены в точках 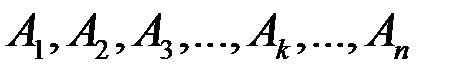 .
.
Найдём равнодействующую 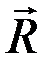 данной системы сил. Для этого сложим вначале силы
данной системы сил. Для этого сложим вначале силы 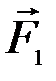 и
и 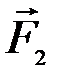 . Модуль равнодействующей системы параллельных сил равен их алгебраической сумме, значит
. Модуль равнодействующей системы параллельных сил равен их алгебраической сумме, значит
 . (4.1)
. (4.1)
Равнодействующая 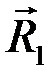 приложена в точке С1, положение которой определим, воспользовавшись теоремой Вариньона о моменте равнодействующей относительно точки С1:
приложена в точке С1, положение которой определим, воспользовавшись теоремой Вариньона о моменте равнодействующей относительно точки С1:
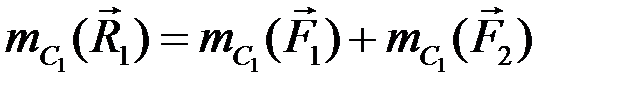 .
.
Так как 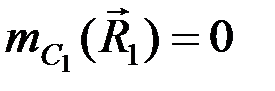 , то получим
, то получим
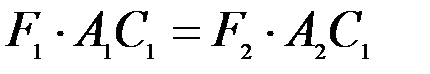 . (4.2)
. (4.2)
Затем найдём равнодействующую 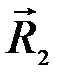 сил
сил 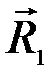 и
и 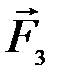
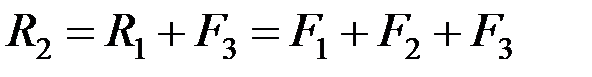 . (4.3)
. (4.3)
Применив для сил 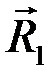 и
и 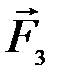 теорему Вариньона о моменте равнодействующей относительно точки С2 , в которой приложена равнодействующая
теорему Вариньона о моменте равнодействующей относительно точки С2 , в которой приложена равнодействующая 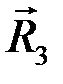 , получим:
, получим:
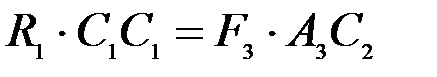 . (4.4)
. (4.4)
Продолжая дальше сложение сил, получим, что модуль равнодействующей R системы параллельных сил равен алгебраической сумме их модулей:
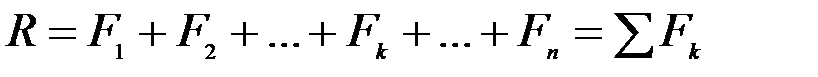 . (4.5)
. (4.5)
Равнодействующая 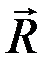 приложена в точке С, которая называется центром параллельных сил.
приложена в точке С, которая называется центром параллельных сил.
Из выражений (4.1) – (4.5) следует, что при повороте в пространстве всех сил системы на один и тот же угол (например, на угол α) получим систему вертикальных сил 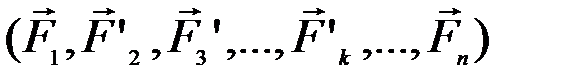 , модуль равнодействующей
, модуль равнодействующей 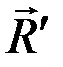 и положение точки С, в которой она приложена, не меняются, так как остаются справедливыми все выражения (4.1) – (4.5).
и положение точки С, в которой она приложена, не меняются, так как остаются справедливыми все выражения (4.1) – (4.5).
Отсюда вытекает основное свойство центра параллельных сил: его положение в пространстве не меняется при повороте всех сил системы на один и тот же угол.
Центром параллельных сил называется точка С, в которой приложена равнодействующая системы параллельных сил и положение которой не меняется при повороте всех сил системы в пространстве на один и тот же угол.
На рис. 63 показаны координаты 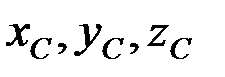 центра параллельных сил С и координаты
центра параллельных сил С и координаты 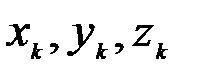 приложения силы
приложения силы 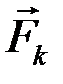 .
.
Для определения координат центра параллельных сил С воспользуемся теоремой Вариньона о моменте равнодействующей. Запишем эту теорему для вертикальных сил 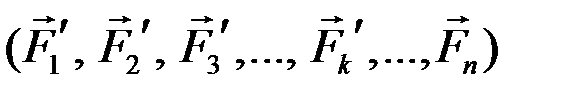 относительно оси Oy:
относительно оси Oy:
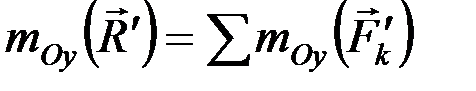 или
или 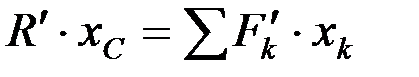 ,
,
откуда 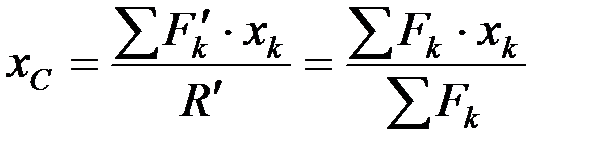 .
.
Относительно оси Ох:
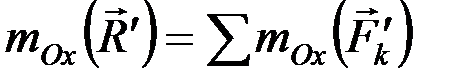 или
или 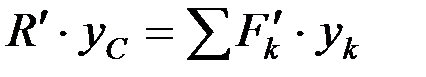 ,
,
откуда 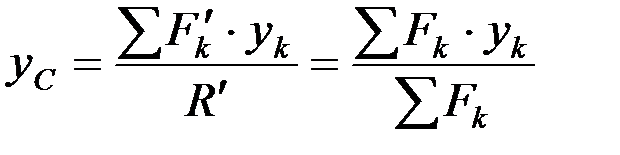 .
.
Для определения координаты  центра параллельных сил воспользуемся основным свойством параллельных сил: поворачиваем (рис. 63) все силы системы на угол
центра параллельных сил воспользуемся основным свойством параллельных сил: поворачиваем (рис. 63) все силы системы на угол 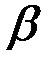 до их горизонтального положения. Получим систему сил
до их горизонтального положения. Получим систему сил 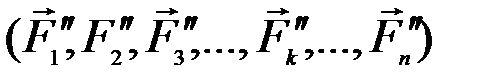 , параллельных оси Ox. Запишем для этой системы сил теорему Вариньона о моменте равнодействующей относительно оси Оу:
, параллельных оси Ox. Запишем для этой системы сил теорему Вариньона о моменте равнодействующей относительно оси Оу:
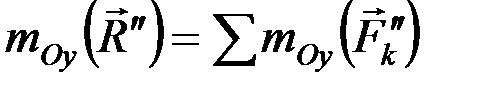 или
или 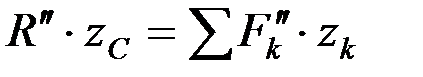 ,
,
откуда 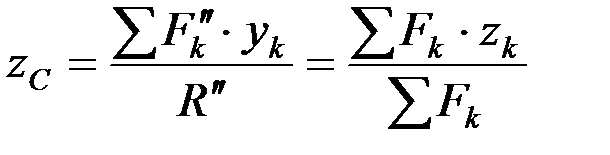 .
.
Таким образом, координаты центра параллельных сил равны
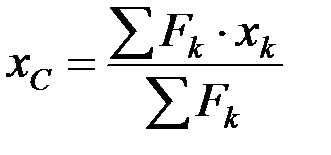 ,
, 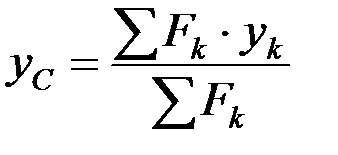 ,
, 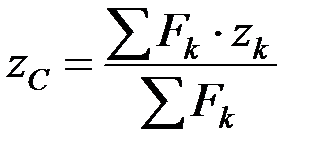 . (4.6)
. (4.6)
Дата добавления: 2016-03-15; просмотров: 731;
