Поступательное и вращательное движения твёрдого тела
Поступательным движением твёрдого тела называется такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе при движении тела.
Поступательно движется, например, кузов экипажа 1 на прямолинейном участке пути (рис. 8).
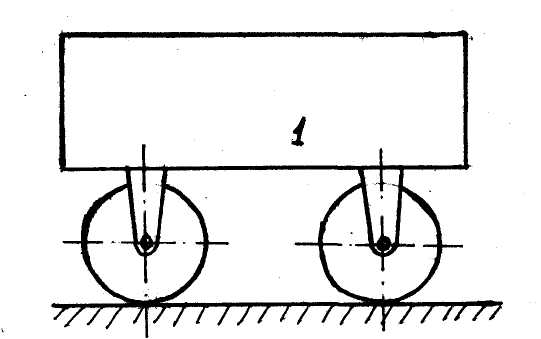
| Рис.8 |
| Рис.9 |
| C |
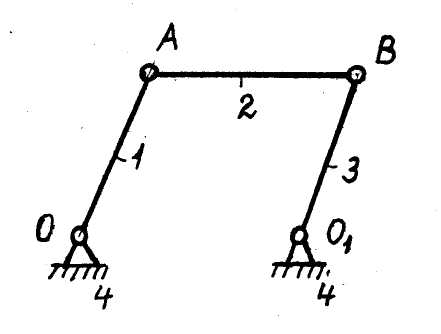
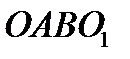 (звено 4 –стойка, неподвижное) (рис. 9), если
(звено 4 –стойка, неподвижное) (рис. 9), если 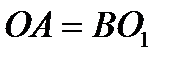 и
и 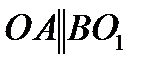 , звено
, звено 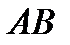 движется поступательно.
движется поступательно.
Основная теорема поступательного движения твёрдого тела
При поступательном движении все точки тела движутся по одинаковым, при наложении совпадающим траекториям и имеют в данный момент времени одинаковые скорости и ускорения по модулю и направлению.
Согласно основной теореме поступательного движения твёрдого тела, для звена 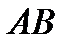 шарнирного четырёхзвенника (рис. 9) выполняются условия:
шарнирного четырёхзвенника (рис. 9) выполняются условия:
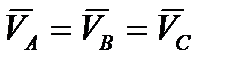 ;
; 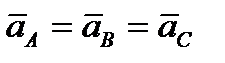 . (2.1)
. (2.1)
Из основной теоремы поступательного движения твёрдого тела следует, что для описания такого движения достаточно задать движение любой точки тела, например центра тяжести 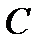 . Тогда выражения
. Тогда выражения
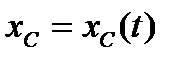 ,
, 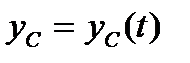 ,
, 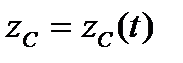 (2.2)
(2.2)
являются уравнениями поступательного движения твёрдого тела.
Вращательным движением твёрдого тела называется такое движение, при котором остаются неподвижными все точки тела, лежащие на некоторой прямой, называемой осью вращения (ось 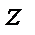 на рис. 10).
на рис. 10).
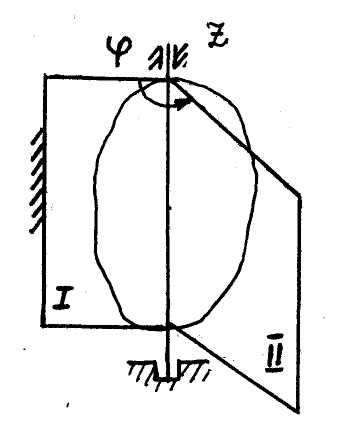 Для задания положения тела при вращательном движении служит угол поворота
Для задания положения тела при вращательном движении служит угол поворота 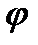 между условно неподвижной плоскостью I (рис. 10) и подвижной плоскостью II , связанной с телом. Угол поворота тела
между условно неподвижной плоскостью I (рис. 10) и подвижной плоскостью II , связанной с телом. Угол поворота тела 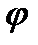 считается положительным, если с конца оси вращения
считается положительным, если с конца оси вращения 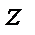 вращение тела представляется происходящим против хода часовой стрелки. Выражение
вращение тела представляется происходящим против хода часовой стрелки. Выражение
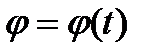 (2.3)
(2.3)
| Рис. 10 |
Угол поворота 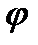 измеряется в радианах. Если тело совершит
измеряется в радианах. Если тело совершит 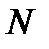 оборотов, то угол его поворота определяется выражением
оборотов, то угол его поворота определяется выражением
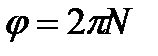 . (2.4)
. (2.4)
Кроме угла поворота 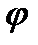 , двумя другими характеристиками вращательного движения, общими для всего тела, являются угловая скорость
, двумя другими характеристиками вращательного движения, общими для всего тела, являются угловая скорость 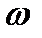 и угловое ускорение
и угловое ускорение 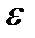 .
.
Угловой скоростью 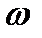 называется величина, характеризующая быстроту изменения угла поворота
называется величина, характеризующая быстроту изменения угла поворота 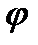 в единицу времени и равная первой производной от
в единицу времени и равная первой производной от 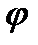 по времени:
по времени:
 . (2.5)
. (2.5)
Угловая скорость 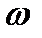 измеряется в рад/с. Если тело совершает
измеряется в рад/с. Если тело совершает 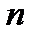 оборотов в минуту (
оборотов в минуту ( 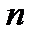 называется частотой вращения тела), то угловая скорость его определяется выражением
называется частотой вращения тела), то угловая скорость его определяется выражением
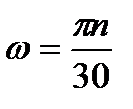 . (2.6)
. (2.6)
Если угловая скорость 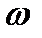 в данный момент времени положительна, т.е. ω>0, то она направлена в сторону заданного направления отсчёта угла
в данный момент времени положительна, т.е. ω>0, то она направлена в сторону заданного направления отсчёта угла 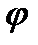 , если ω<0, то – в противоположную сторону.
, если ω<0, то – в противоположную сторону.
Угловым ускорением 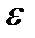 называется величина, характеризующая быстроту изменения угловой скорости в единицу времени и равная первой производной от угловой скорости
называется величина, характеризующая быстроту изменения угловой скорости в единицу времени и равная первой производной от угловой скорости 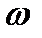 по времени или второй производной от угла поворота
по времени или второй производной от угла поворота 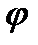 по времени:
по времени:
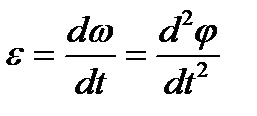 . (2.7)
. (2.7)
Угловое ускорение 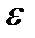 измеряется в рад/с².
измеряется в рад/с².
Если в данный момент времени 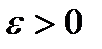 , то оно направлено в сторону заданного направления отсчёта угла поворота φ, если
, то оно направлено в сторону заданного направления отсчёта угла поворота φ, если 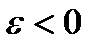 – в противоположную сторону.
– в противоположную сторону.
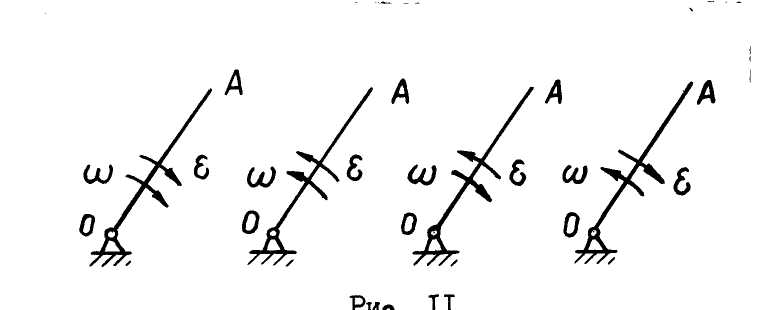
| г) |
| а) |
| в) |
| б) |
| Рис. 11 |
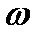 и
и 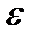 совпадают, тело вращается ускоренно, если не совпадают – замедленно. На рис. 11а,б показаны случаи ускоренного вращения тела
совпадают, тело вращается ускоренно, если не совпадают – замедленно. На рис. 11а,б показаны случаи ускоренного вращения тела 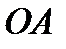 вокруг оси
вокруг оси  , на рис. 11в,г – случаи замедленного вращения.
, на рис. 11в,г – случаи замедленного вращения.
Рассмотрим частные случаи вращательного движения твёрдого тела.
1. Равномерное вращение тела. В этом случае угловая скорость тела 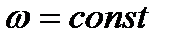 . Тогда угловое ускорение
. Тогда угловое ускорение  . Учитывая, что
. Учитывая, что 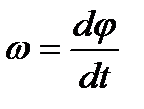 ,получаем:
,получаем: 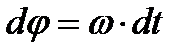 . Интегрируя данное выражение
. Интегрируя данное выражение 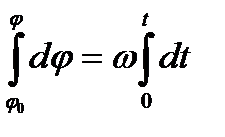 ,получаем:
,получаем:
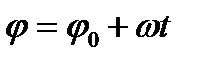 , (2.8)
, (2.8)
где 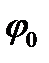 – угол поворота тела при
– угол поворота тела при 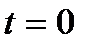 .
.
Выражение (2.8) является законом равномерного вращения твёрдого тела.
2. Равнопеременное вращение тела. В этом случае угловое ускорение  (знак «+» относится к случаю ускоренного вращения, знак «–» – замедленного). Учитывая, что
(знак «+» относится к случаю ускоренного вращения, знак «–» – замедленного). Учитывая, что  , получаем:
, получаем: 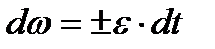 . Интегрируем данное выражение
. Интегрируем данное выражение 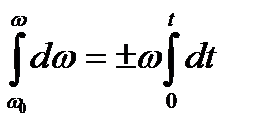 . Получаем
. Получаем
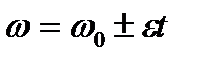 , (2.9)
, (2.9)
где 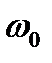 – угловая скорость тела при
– угловая скорость тела при  .
.
После повторного интегрирования получим
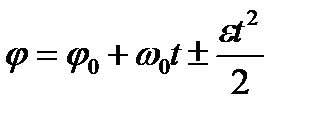 . (2.10)
. (2.10)
Выражения (2.9) и (2.10) определяют законы изменения угловой скорости и угла поворота в случае равнопеременного вращения твёрдого тела.
3. Общий случай вращательного движения тела. В этом случае угловое ускорение тела 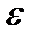 является функцией времени
является функцией времени 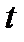
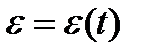 . (2.11)
. (2.11)
После интегрирования выражения (2.11) (см. случаи 1 и 2) получаем закон изменения угловой скорости
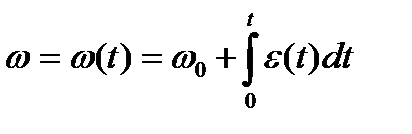 . (2.12)
. (2.12)
После интегрирования выражения (1.12) найдём закон вращения тела в рассматриваемом случае
 . (2.13)
. (2.13)
При вращательном движении модуль скорости любой точки  (рис. 12) тела равен
(рис. 12) тела равен
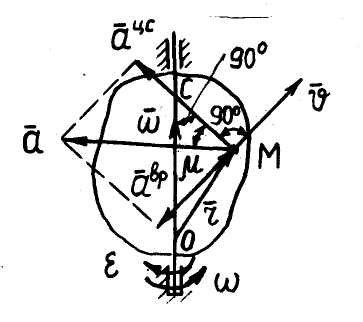
| Рис.12 |
 . (2.14)
. (2.14)
В выражении (2.14)  – радиус вращения точки – перпендикуляр, опущенный из точки
– радиус вращения точки – перпендикуляр, опущенный из точки  на ось вращения.
на ось вращения.
Вектор скорости 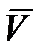 лежит в плоскости траектории точки
лежит в плоскости траектории точки  и направлен перпендикулярно радиусу вращения
и направлен перпендикулярно радиусу вращения 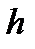 в сторону круговой стрелки
в сторону круговой стрелки 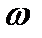 .
.
Указанные модуль и направление вектора скорости 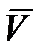 можно получить из векторной формулы (2.15) (формула Эйлера), которая справедлива в случае вращательного движения тела, так как радиус-вектор
можно получить из векторной формулы (2.15) (формула Эйлера), которая справедлива в случае вращательного движения тела, так как радиус-вектор 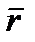 (рис. 12), проведенный из некоторой точки
(рис. 12), проведенный из некоторой точки  в точку
в точку  , при вращении тела меняется только по направлению (модуль
, при вращении тела меняется только по направлению (модуль 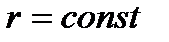 ):
):
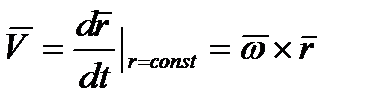 , (2.15)
, (2.15)
где 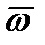 – вектор угловой скорости.
– вектор угловой скорости.
Вектор 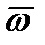 направляется по оси вращения в соответствии с правилом правого винта, прикладывается в любой точке оси вращения (т.е.
направляется по оси вращения в соответствии с правилом правого винта, прикладывается в любой точке оси вращения (т.е.  скользящий вектор).
скользящий вектор).
Ускорение 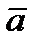 точки
точки  тела при вращательном движении определяется как геометрическая сумма
тела при вращательном движении определяется как геометрическая сумма
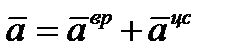 , (2.16)
, (2.16)
где 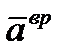 – вращательное ускорение;
– вращательное ускорение; 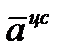 – центростремительное ускорение. Векторы
– центростремительное ускорение. Векторы 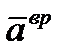 и
и 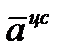 лежат в плоскости траектории точки
лежат в плоскости траектории точки  . Модули этих векторов определяются выражениями:
. Модули этих векторов определяются выражениями:
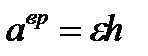 ; (2.17)
; (2.17)
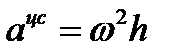 . (2.18)
. (2.18)
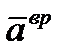 направлен
направлен 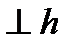 в сторону круговой стрелки
в сторону круговой стрелки 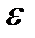 ,
, 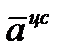 – по
– по 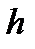 к оси вращения. Так как
к оси вращения. Так как 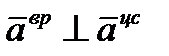 , то модуль полного ускорения
, то модуль полного ускорения 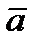 равен
равен
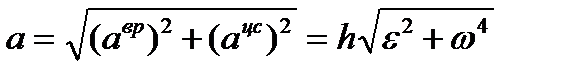 .
.
Из выражения (2.16) следует, что направление вектора ускорения 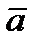 (рис. 12) определяется диагональю параллелограмма, построенного на векторах
(рис. 12) определяется диагональю параллелограмма, построенного на векторах 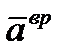 и
и 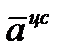 как на сторонах.
как на сторонах.
На рис. 12  – угол между вектором
– угол между вектором 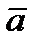 и радиусом
и радиусом 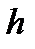 . Из рисунка видно, что
. Из рисунка видно, что 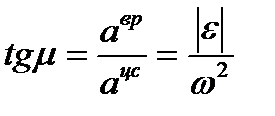 , откуда
, откуда 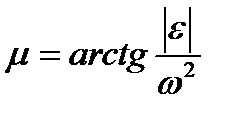 ,
,
при этом 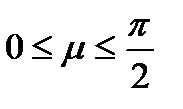 . (2.19)
. (2.19)
Согласно выражению (2.19), векторы ускорения всех точек тела при вращательном движении наклонены к соответствующим радиусам вращения под одним и тем же углом 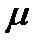 .
.
Рассмотрим наиболее характерные примеры решения задач на вращательное движение тела.
| Рис.13 |
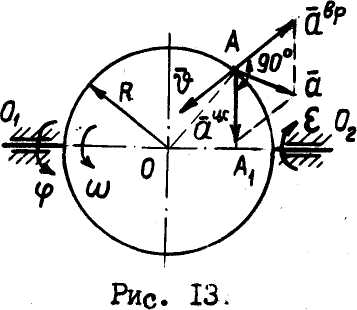 Пример 1. Диск (рис. 13) радиусом
Пример 1. Диск (рис. 13) радиусом 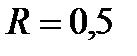 м вращается по закону
м вращается по закону 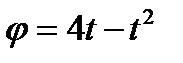 (
( 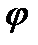 – в радианах,
– в радианах, 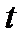 – в секундах) относительно оси
– в секундах) относительно оси  , совпадающей с его горизонтальным диаметром. Для момента времени
, совпадающей с его горизонтальным диаметром. Для момента времени  с определить скорость и ускорение точки
с определить скорость и ускорение точки 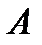 обода диска.
обода диска.
Находим угловую скорость 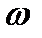 и угловое ускорение
и угловое ускорение 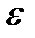 диска в заданный момент времени
диска в заданный момент времени
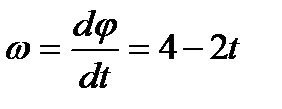 .
.
При 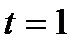 с
с 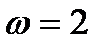 рад/с. Так как при
рад/с. Так как при 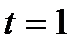 с
с 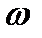 положительная, то она направлена в сторону отсчёта
положительная, то она направлена в сторону отсчёта 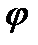
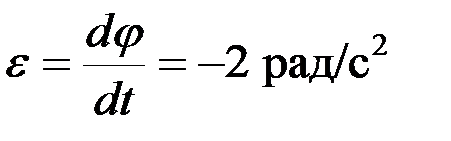 .
.
Знак «–» указывает на то, что 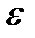 направлено против заданного направления отсчета угла
направлено против заданного направления отсчета угла 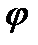 . Скорость точки
. Скорость точки 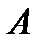 обода равна
обода равна
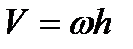 ,
,
где 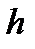 – радиус вращения точки; из рисунка видно, что
– радиус вращения точки; из рисунка видно, что
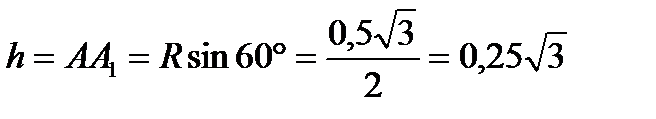 м.
м.
Тогда 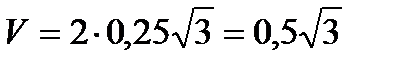 м/с.
м/с.
Вектор 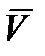 направлен
направлен 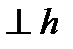 в сторону круговой стрелки
в сторону круговой стрелки 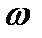 (на нас). Ускорение точки равно
(на нас). Ускорение точки равно
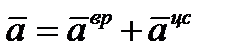 .
.
Вращательное ускорение
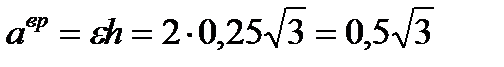 м/с².
м/с².
Вектор 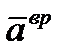 направлен
направлен  в сторону круговой стрелки
в сторону круговой стрелки 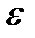 (от нас).
(от нас).
Центростремительное ускорение
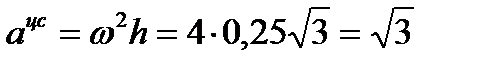 м/с².
м/с².
Вектор 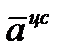 направлен вдоль
направлен вдоль 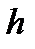 от точки
от точки 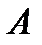 к оси вращения.
к оси вращения.
Ускорение точки 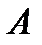 равно
равно
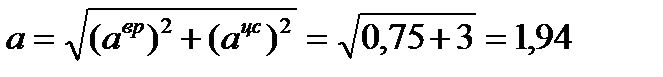 м/с².
м/с².
Вектор 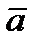 направлен по диагонали параллелограмма, построенного на векторах
направлен по диагонали параллелограмма, построенного на векторах 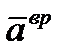 и
и 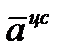 .
.
Пример 2. Кривошип 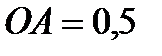 ммеханизма шарнирного четырёхзвенника
ммеханизма шарнирного четырёхзвенника  (рис. 14) вращается вокруг оси
(рис. 14) вращается вокруг оси  , имея в заданном положении угловую скорость
, имея в заданном положении угловую скорость 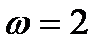 рад/си угловое ускорение
рад/си угловое ускорение 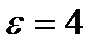 рад/с².
рад/с².
| Рис. 14 |
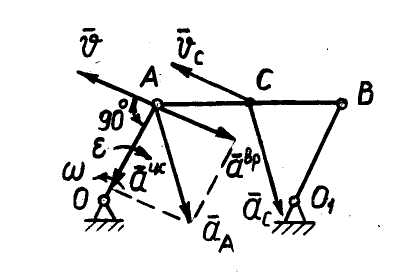 Определить скорость и ускорение центра тяжести
Определить скорость и ускорение центра тяжести 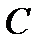 звена
звена 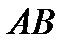 механизма, если
механизма, если 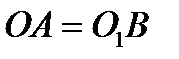 ,
, 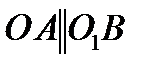 и
и 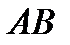 – однородный стержень.
– однородный стержень.
Поскольку звено 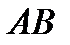 однородное, его центр тяжести
однородное, его центр тяжести 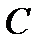 находится посередине стержня
находится посередине стержня 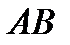 . С учётом того что
. С учётом того что 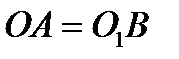 и
и 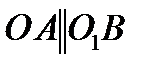 , звено
, звено 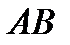 механизма движется поступательно. Поэтому из основной теоремы поступательного движения следует, что
механизма движется поступательно. Поэтому из основной теоремы поступательного движения следует, что
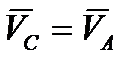 и
и  .
.
Скорость 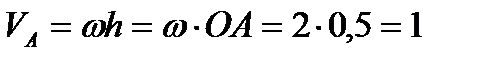 м/с;
м/с; 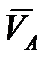 направлен
направлен  в сторону
в сторону  .
.
Ускорение 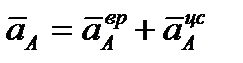 ,
,
где 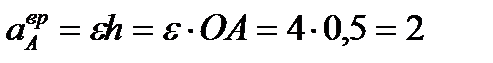 м/с²;
м/с²;  направлен
направлен 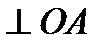 в сторону
в сторону 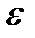 ;
; 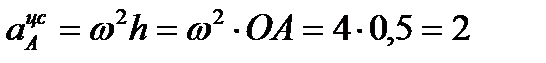 м/с²;
м/с²; 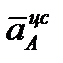 направлен по
направлен по 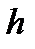 к оси вращения
к оси вращения  .
.
Тогда  м/с².
м/с².
Вектор 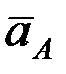 направлен по диагонали параллелограмма, построенного на векторах
направлен по диагонали параллелограмма, построенного на векторах 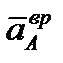 и
и 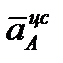 .
.
Следовательно, 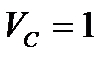 м/с;
м/с; 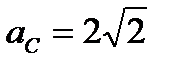 м/с².Векторы
м/с².Векторы 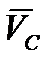 и
и 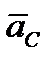 направлены параллельно соответственно векторам
направлены параллельно соответственно векторам 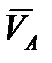 и
и 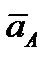 .
.
Пример 3. Диск начинает вращаться равноускоренно из состояния покоя, сделав за первые две секунды 10 оборотов. Определить угловую скорость 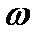 , угловое ускорение
, угловое ускорение 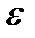 диска при
диска при 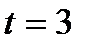 с.
с.
При решении задач на частные случаи вращения тела необходимо записать выражения, по которым определяются угловая скорость 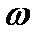 и угол поворота
и угол поворота 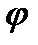 для случая вращения тела, рассматриваемого в конкретном примере. Поскольку в данном примере диск вращается равноускоренно, то
для случая вращения тела, рассматриваемого в конкретном примере. Поскольку в данном примере диск вращается равноускоренно, то
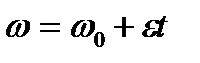 и
и 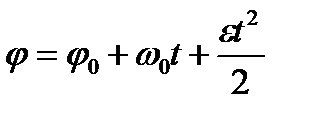 .
.
По условию задачи 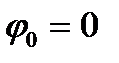 ,
, 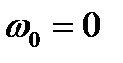 , так как вращение диска начинается из состояния покоя. Тогда в рассматриваемом случае
, так как вращение диска начинается из состояния покоя. Тогда в рассматриваемом случае
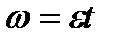 ,
, 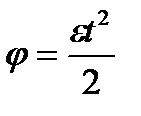 .
.
Угол поворота 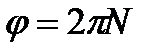 , где
, где 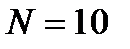 оборотов. Тогда угловое ускорение
оборотов. Тогда угловое ускорение
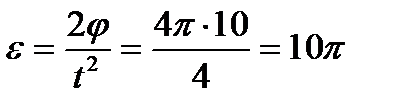 рад/с².
рад/с².
При 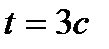 угловая скорость диска
угловая скорость диска 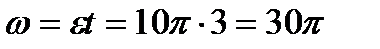 рад/си
рад/си 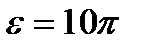 рад/с.
рад/с.
Пример 4. Тело вращается вокруг неподвижной оси с угловым ускорением 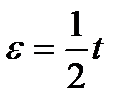 рад/с². Определить законы изменения угловой скорости
рад/с². Определить законы изменения угловой скорости 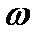 и угла поворота
и угла поворота 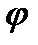 тела, считая, что вращение начинается из состояния покоя и угол поворота
тела, считая, что вращение начинается из состояния покоя и угол поворота 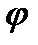 отсчитывается от начального положения тела.
отсчитывается от начального положения тела.
Данный пример относится к общему случаю вращения твёрдого тела, поэтому законы изменения 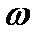 и
и 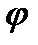 находим по выражениям (1.12) и (1.13)
находим по выражениям (1.12) и (1.13)
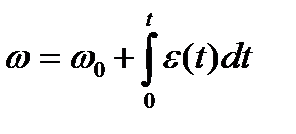 ,
,  .
.
По условию задачи 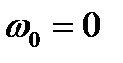 ,
, 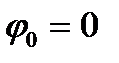 .
.
Тогда угловая скорость тела
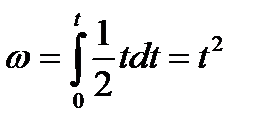 .
.
Закон вращения тела: 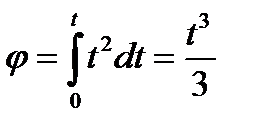 .
.
Дата добавления: 2016-03-15; просмотров: 1004;
