Числовые характеристики системы двух
Случайных величин
Зная законы распределения составляющих для дискретных двумерных величин или плотности их распределения для непрерывных, математическое ожидание и дисперсию составляющих можно найти по известным формулам:
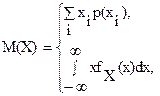 ,
, 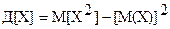
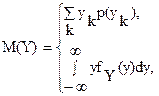 .
. 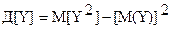
Зная условные законы распределения составляющих, можно найти условные математические ожидания по формулам:
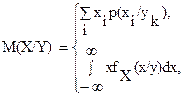
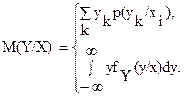
Степень статистической зависимости двух случайных величин X,Y характеризуется числовой характеристикой, называемой корреляционным моментом, и вычисляется по формуле:
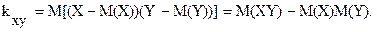
Коэффициентом корреляции величин X Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
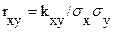
Пример 18. Для дискретной двумерной величины, заданной в примере 10? найти: а) математические ожидания составляющих; б) дисперсии составляющих; в) условное математическое ожидание X при условии, что Y=-2; г) корреляционный момент.
Решение. При решении примера получены законы распределения Х (1 и 4 строки), Y (1 и 5 столбцы), условный закон распределения Х, при условии, что Y=-2 (1 и 5 столбцы):
| xi | -1 | ||
| P(xi) | 0,3 | 0,3 | 0,4 |
| хi | -1 | |||||
| p(xi) | 0,3 | 0,3 | 0,4 | |||
| yk | -2 | |||||
| P(yk) | 0,45 | 0,55 | ||||
| хi | -1 | ||
| p(xi/у=-2) | 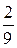
| 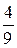
| 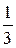
|
а) из первой и второй таблицы получаем:
| Yk | -2 | |
| P(Yk) | 0,45 | 0,55 |
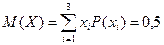 ;
; 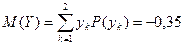 .
.
б) 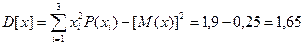 ,
,
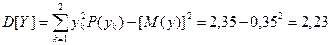 .
.
в) Из третьей таблицы:
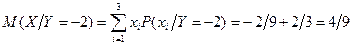
г) По определению
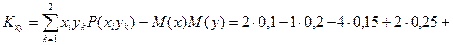
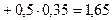 .
.
Пример 19. Плотность распределения вероятностей случайного вектора (X,Y) имеет вид:
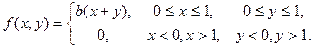
Найти: а) постоянную b; б) безусловные и условные плотности распределения составляющих; в) математические ожидания и дисперсии для Х и Y; г) условное математическое ожидание M(X/Y); д) коэффициент корреляции.
Решение. а) Используем второе свойство двумерной плотности вероятности:
. 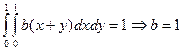
б) По четвертому свойству:
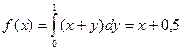 ;
; 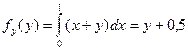 .
.
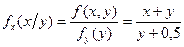 ;
;  .
.
Заметим, что условные плотности распределения не совпадают с безусловными, следовательно X и Y зависимы.
в) Математические ожидания и дисперсии находятся так же, как в одномерном случае.
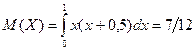 ;
; 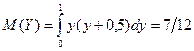 ;
;
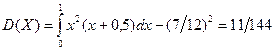 ;
;
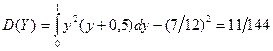 .
.
г) Для отыскания условного математического ожидания используем условную плотность распределения:
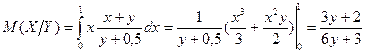 .
.
д) По определению:
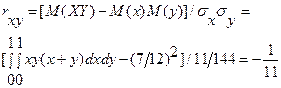 .
.
20. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y): f(x, у)= =2cos(x)cos(y) в квадрате 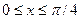 ,
, 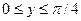 ; вне квадрата f(x,y)= 0. Найти математические ожидания составляющих.
; вне квадрата f(x,y)= 0. Найти математические ожидания составляющих.
21. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y): f(x,y)= =(1/2)sin(x+y) в квадрате 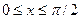 ,
, 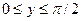 ; вне квадрата f(x,y)=0. Найти математические ожидания и дисперсии составляющих.
; вне квадрата f(x,y)=0. Найти математические ожидания и дисперсии составляющих.
22. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y): F(x,y)=(l/4)sin(x)sin(y) в квадрате 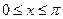 ,
, 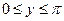 ; вне квадрата f(x,y)=0. Найти: а) математические ожидания и дисперсии составляющих; б) корреляционный момент.
; вне квадрата f(x,y)=0. Найти: а) математические ожидания и дисперсии составляющих; б) корреляционный момент.
23. Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна p. Случайные величины: Х – число выстрелов до первого попадания (включительно), Y – число промахов. а) Описать закон распределения случайного вектора (Х, Y) и законы распределения каждой компоненты.
б) Вычислить вероятность Р {Х= Y}.
в) Вычислить коэффициент корреляции .
г) Определить, зависимы или независимы компоненты Х и Y.
д) Найти, условное математическое ожидание случайной величины Х при условии, что Y приняла значение 2.
24. Число Х выбирается случайным образом из множества целых чисел {1,2,3}. Затем из того же множества выбирается наудачу число Y, большее первого или равное ему.
а) Описать закон распределения случайного вектора (Х, Y).
б) Определить, зависимы или независимы случайные компоненты Х и Y.
в) Построить условный закон распределения компоненты Х при условии, что Y приняло значение, равное 2.
г) Вычислить основные характеристики: mx, my, Dx, Dy, Kxy, .
25. Плотность распределения вероятностей случайного вектора (X,Y) имеет вид:
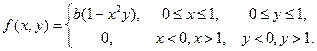
Найти: а) постоянную b; б) безусловные и условные плотности распределения компонент; в) математические ожидания и дисперсии X и Y; г) условные математические ожидания M(X/Y); д) корреляционный момент.
26. Плотность распределения вероятностей случайного вектора (X,Y) имеет вид:
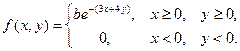
Найти: а) постоянную b; б) безусловные и условные плотности распределения составляющих; в) вероятность того, что X>1/2, а Y>1/4; г) математические ожидания, дисперсии, коеффицент корреляции Х и У.
Разные задачи
27. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди взятых 6 деталей 4 – стандартные.
28. Участники жеребьёвки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого случайно извлечённого жетона не содержит цифры 5.
29. В урне 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: О, П, Р, С, Т. Найти вероятность того, что на вытянутых по одному и расположенных в одну линию кубиках можно будет прочесть слово “спорт”.
30. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наугад извлечённый кубик будет иметь окрашенных граней: а) 1; б) 2; в) 3.
31. На отдельных карточках написаны цифры: 1; 2; 3; 4; 5; 6; 7; 8; 9. Последовательно без возвращения выбирают и раскладывают 4 карточки. Какова вероятность получить: а) число 1234; б) любое четырехзначное чётное число из указанных цифр?
32. Замок содержит на общей оси 5 дисков, каждый из которых разделен на 6 секторов с написанными на них различными цифрами. Замок открывается только в том случае, если каждый диск занимает определённое положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.
33. Восемь различных книг расставляют случайным образом на полке. Найти вероятность того, что 2 определённые книги окажутся поставленными рядом.
34. Десять различных книг расставляют в случайном порядке на полке. Определить вероятность того, что при этом 3 определённые книги окажутся поставленными рядом.
35. Найти вероятность того, что при случайном распределении 3 шаров по 3 урнам все урны будут заняты (шары, так же как и урны, отличаются друг от друга: например, урны пронумерованы, а шары разных цветов).
36. Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наугад 5 билетов а) 1 выигрышный, б) оба выигрышных, в) хотя бы один выигрышный.
37. Для проверки 6 магазинов нужны 3 ревизора, каждый из которых должен проверить 2 магазина. Какова вероятность того, что при случайном распределении объектов первый ревизор будет проверять определённые 2 магазина?
38. В лотерее n билетов, из которых m выигрышных. Какова вероятность выиграть хотя бы один раз, имея k билетов?
39. 5 мужчин и 10 женщин случайным образом образуют 5 групп по 3 человека. Найти вероятность того, что в каждой группе будет 1 мужчина.
40. Лифт с 4 пассажирами останавливается на 10 этажах. Какова вероятность того, что 2 пассажира не выйдут на одном этаже?
41. Брошены 2 игральные кости. Какова вероятность того, что номер 6 выпадет хотя бы на одной из них?
42. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наугад извлечённых 2 деталей хотя бы 1 стандартная.
43. Ящик содержит 10 деталей, среди которых 2 нестандартные. Найти вероятность того, что в случайно выбранных 6 деталях окажется не более 1 нестандартной.
44. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна 0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела дали попадание.
45. В 2 ящиках находятся детали: в первом 10 (из них 3 стандартные), во втором - 45 (из них 6 стандартных). Из каждого ящика наугад вынимают по 1 детали. Найти вероятность того, что обе детали окажутся стандартными.
46. В студии телевидения 3 телевизионные камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы 1 камера.
47. Чему равна вероятность того, что при бросании 3 игральных костей 6 очков будет хотя бы на 1 из игральных костей?
48. Предприятие изготовляет 95% стандартных изделий, причем 86% из них первого сорта. Найти вероятность того, что взятое наугад изделие, изготовленное на этом предприятии, окажется первого сорта.
49. Из цифр 1; 2; 3; 4; 5 сначала выбирают одну, а затем — еще одну цифру. Предположим, что все 20 возможных исходов равновероятны. Найти вероятность того, что будет выбрана нечетная цифра а) первый раз, б) второй раз, в) оба раза.
50. Вероятность того, что событие А появится хотя бы 1 раз в 2 независимых испытаниях, равна 0,75. Найти вероятность появления события в одном испытании (предполагается, что вероятность появления события в обоих испытаниях одна и та же).
51. Вероятность поражения цели первым стрелком при 1 выстреле равна 0,8, вторым стрелком - 0,6. Найти вероятность того, что цель будет поражена только одним стрелком, если каждый сделал по выстрелу.
52. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие нестандартно, равна 0,1. Найти вероятность того, что: а) из трех проверенных изделий нестандартно только одно, б) нестандартным окажется только четвертое по порядку проверенное изделие.
53. Вероятность того, что в результате 4 независимых опытов событие А произойдет хотя бы один раз, равна 1/2. Определить вероятность появления события в одном опыте, если она во всех опытах остается неизменной.
54.Три электрические лампочки последовательно включены в цепь. Вероятность того, что одна (любая) лампочка перегорит, если напряжение в сети превысит номинальное, равна 0,6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет, если лампочки перегорают независимо друг от друга.
55. Три электрические лампочки, 2 из которых соединены параллельно, а третья с ними последовательно, включены в цепь. Вероятность того, что 1 (любая) лампочка перегорит, если напряжение в сети превысит номинальное, равна 0,6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет, если лампочки перегорают независимо друг от друга.
56. У сборщика имеется 16 деталей, изготовленных заводом № 1, и 4 детали, изготовленные заводом № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1.
57. Два стрелка произвели по 1 выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым - 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень.
58. В урне 5 белых и 3 черных шара. Из урны извлекают подряд 4 шара. Определить вероятность того, что будут извлечены 2 черных и 2 белых шара.
59. Лифт отправляется с r= 7 пассажирами и останавливается на n = 10 этажах. Чему равна вероятность того, что никакие два пассажира не выйдут на одном и том же этаже? (Предполагается, что способы распределения пассажиров по этажам равновероятны.).
60. Дни рождения. Какова вероятность того, что у r наудачу взятых людейдни рождения окажутся различными? (Предполагается, что распределение дней рождения по дням года равновероятно.)
61. Бросаются шесть симметричных игральных костей. Какова вероятность того, что выпадут все грани?
62. В городе в течение недели произошло семь пожаров. Какова вероятность того, что все пожары приходились на разные дни недели?
63. r шаров случайным образом размещаются по п ящикам. Какова вероятность того, что заданный ящик содержит i шаров, i = 0, r ?
64. В урне имеется 10 шаров: 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность того, что этот шар: а) белый; б) черный?
65. Из слова НАУГАД выбирается наугад одна буква. Какова вероятность того, что это буква А? Какова вероятность того, что это гласная?
66. При стрельбе была получена частота попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов?
67. Брошены две игральные кости. Какова вероятность выпадения на двух костях в сумме не менее 9 очков? Какова вероятность выпадания единицы, по крайней мере на одной кости?
68. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово ДВА?
69. В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два шара окажутся черными?
70. Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слова МАМА?
71. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.
72. В лотерее n билетов, из которых n выгрышных. Участник лотереи покупает kбилетов. Определить вероятность того, что он выиграет хотя бы на один билет.
73. Среди 25 экзаменационных билетов 5 "хороших". Два студента по очереди берут по одному билету. Найти вероятности следующих событий:
А ={первый студент взял хороший билет}; В = {второй студент взял хороший билет}; С = {оба студента взяли хорошие билеты}.
74. (Задача о выборке.) В партии из 50 изделий 5 бракованных. Из партии выбираются наугад 6 изделий. Определить вероятность того, что среди этих 6 изделий 2 окажутся бракованными.
75. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.
76. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей начиная со второго. Найти вероятности следующих событий:
A ={все пассажиры выйдут на четвертом этаже}; В ={все пассажиры выйдут одновременно (на одном и том же этаже)};
77. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-м и 55-м километрами линии?
78. Шар х2 + у2 + z2 = З2 помещен внутри эллипсоида 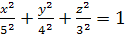 . Найти вероятность того, что поставленная наудачу внутри эллипсоида точка окажется внутри шара.
. Найти вероятность того, что поставленная наудачу внутри эллипсоида точка окажется внутри шара.
79. Вероятность того, что в течение одной смены возникнет неполадка станка, равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за три смены?
80. В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
81. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос?
82. В круг радиуса Rвписан квадрат. Чему равна вероятность того, что поставленные наудачу внутри круга 2 точки окажутся внутри квадрата?
83. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель 0,7, для второго — 0,8. Какова вероятность попадания в волка (хотя бы при одном выстреле)? Как изменится результат, если охотники сделают по два выстрела?
84. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму равна: для лыжника - 0,9, для велосипедиста - 0,8, для бегуна - 0,75. Найти вероятность того, что спортсмен, вызванный наугад, выполнит норму.
85. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что стандартна деталь завода № 1, равна 0,8, завода № 2 - 0,9. Сборщик наудачу извлек деталь изнаугад взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
86. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором 30 деталей, из них 24 стандартных, в третьем - 10 деталей, из них 6 стандартных. Найти вероятность того, что случайным образом извлеченная деталь из наугад взятого ящика стандартна.
87. В телевизионном ателье 4 кинескопа. Вероятности того, что кинескопы выдержат гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что наудачу взятый кинескоп выдержит гарантийный срок службы.
88. В 2 ящиках имеются радиолампы: в первом ящике их 12, из них 1 нестандартная, во втором - 10, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй ящик. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет стандартной.
89. В ящик, содержащий 3 одинаковые детали, брошена стандартная деталь, а затем наудачу извлечена 1 деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находившихся в ящике.
90. В ящике 15 теннисных мячей, из которых 9 новых. Для первой игры наугад берут 3 мяча, которые после игры возвращают в ящик и считают неновыми. Для второй игры также наугад берут 3 мяча. Найти вероятность того, что асе мячи, взятые для второй игры, новые.
91. Трое охотников одновременно выстрелили по вепрю, который был убит одной пулей. Определить вероятность того, что вепрь убит первым, вторым или . третьим охотником, если вероятности попадания для них равны соответственно 0,2; 0,4; 0,6.
92. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4 студента, из второй I - 6 студентов, из третьей - 5. Вероятности того, что студент из первой, второй и третьей групп попадет в сборную института, соответственно равны 0,9; 0,7; 0,8. Один из отобранных студентов в итоге соревнования попал в сборную. К какой группе вероятнее всего он принадлежит?
93. При отклонении от нормального режима работы автомата сигнализатор С - I срабатывает с вероятностью 0,8, а сигнализатор С- II - с вероятностью I. Вероятности того, что автомат снабжен сигнализатором С - I или С - II, соответственно равны 0,6 и 0,4. Получен сигнал о разладке автомата. Что вероятнее: автомат снабжен сигнализатором С - I или С - II?
94. Из партии, содержащей 5 изделий, наудачу взято 1 изделие, оказавшееся бракованным. Количество бракованных изделий равновозможно любое. Какое предположение о количестве бракованных изделий наиболее вероятно?
95. Вероятность для изделия некоторого производства удовлетворять стандарту равна 0,96. Предложена упрощенная система проверки на стандартность, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, и 0,05 для изделий, не удовлетворяющих ему. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно таково.
96. В первой урне имеется 1 белый и 9 черных шаров, во второй урне — 1 черный и 5 белых шаров. Наудачу выбирается урна и из нее извлекается шар. Какова вероятность того, что извлеченный шар — черный? Если извлечен черный шар, то какова вероятность того, что он был извлечен из первой урны?
97. В первой урне имеется 1 белый и 9 черных шаров, во второй урне — 1 черный и 5 белых шаров. Из каждой урны случайным образом удалили по одному шару. Оставшиеся шары ссыпали в одну урну, после чего из нее извлекли наудачу шар. Какова вероятность того, что извлеченный шар — белый?
98. Поиск неисправности. На изделии может возникнуть три неисправности. За определенный промежуток времени вероятности возникновения неисправностей соответственно составляют 0.2, 0.15, 0.1. После возникновения первой неисправности изделие отказывает с вероятностью 0.8, второй — с вероятностью 0.5 и третьей — с вероятностью 0.9. Найти вероятность отказа изделия, предполагая возникновение неисправностей несовместными событиями. В какой последовательности следует искать неисправность, явившуюся причиной отказа?
99. Имеется 5 урн. В первых трех урнах находится по два белых и три красных шара, в четвертой и пятой — по одному белому и одному красному шару. Случайно выбирается урна и из нее извлекается шар. Какова условная вероятностьтого, что выбрана четвертая или пятая урны, если извлеченный шар оказалсябелым ?
100. Имеется два одинаковых ящика с шарами. В первом ящике 2 белых и 1 черный шар, во втором — 1 белый и 4 черных шара. Наудачу выбирают один ящик и вынимают из него шар. Какова вероятность, что вынутый шар окажется белым?
101. В цехе работают 20 станков. Из них 10 марки А, 6 марки Ви 4 марки С. Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна 0,9; 0,8 и 0,7. Какой процент отличных деталей выпускает цех в целом?
102. Имеются две урны: в первой 3 белых шара и 2 черных; во второй 4 белых и 4 черных. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
103. Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? (Считать, что мужчин и женщин одинаковое число.)
104. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго — 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что в мишень попал первый стрелок.
105. На фабрике, изготовляющей болты, первая машина производит 25%, вторая — 35%, третья — 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%.
а) Какова вероятность того, что случайно выбранный болт дефектный?
б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной?
106. При передаче сообщения по каналу связи вероятность искажения одного знака равна 1/10. Какова вероятность того, что сообщение из 10 знаков: а) не будет искажено; б) содержит ровно 3 искажения; в) содержит не более трех искажений?
107. Система состоит из п идентичных элементов. Каждый элемент независимо от других за рассматриваемый период времени отказывает с вероятностью р. Система является работоспособной, если не отказали k элементов или более. Какова вероятность того, что система будет работоспособна? Найти минимальное п, при котором эта вероятность будет не ниже 0,9, если р = 0,8, k = 4.
108. По каналу связи передаются сообщения из нулей и единиц. Из-за помех вероятность передачи правильного сообщения равна 0,55. Для повышения вероятности правильной передачи каждый знак сообщения повторяется п раз. За передаваемый принимают знак, повторяющийся в полученном сообщении наибольшее число раз. Найти вероятность правильной передачи одного знака при п-кратном повторении, если п = 5. Подобрать кратность передачи знака п так, чтобы эта вероятность была не ниже 0,99.
109. По каналу связи передается 1000 знаков. Каждый знак может быть искажен независимо от других с вероятностью 0,005. Найти приближенное значение вероятности того, что будет искажено не более трех знаков.
110. По каналу связи передается одна из последовательностей букв АААА, ББББ, ВВВВ с вероятностями р1, р2 и р3 (р1 + р2 + р3 = 1)- Каждая передаваемая буква принимается правильно с вероятностью α и с одинаковой вероятностью (1- α)/2 принимается за две другие буквы. Предполагается, что буквы искажаются независимо друг от друга. Какова вероятность того, что передана последовательность АААА, если принята АВБА?
111. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?
112. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): три партии из четырех или пять из восьми?
113. Изделия некоторого производства содержат 5% брака. Найти! вероятность того, что среди пяти взятых наугад изделий:
а) нет ни одного испорченного;
б) будут два испорченных.
114. Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди пяти случайно выбранных волокон смеси обнаружить менее двух окрашенных?
115. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их количество равно 7.
116. Батарея дала 14 выстрелов по объекту, вероятность попадания в который равна 0,2. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.
117. Вероятность попадания в цель при каждом выстреле из орудия равна 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20?
118. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех?
119. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет на пяти веретенах.
120. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух пуль и более, если число выстрелов равно 5000.
121. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность, что в течение часа позвонят 5 абонентов?
Имеется общество из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна 1/365.
122. Вероятность появления успеха в каждом испытании равна 0,25. Какова вероятность, что при 300 испытаниях успех наступит: а) ровно 75 раз? 6) ровно 85 раз?
123. Какова вероятность того, что в столбике из 100 наугад отобранных монет число монет, расположенных "гербом" вверх, будет от 45 до 55?
124. Производство дает 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не больше 17?
125. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших будет заключено между 790 и 830.
126. При изготовлении гермоблоков РЭА годная продукция составляет 95%. Брак по герметизации составляет 3%, брак по выходным параметрам — 4,5%. Определить коэффициент корреляции двух видов дефектов.
Решение. Введем случайную величину х, которая принимает значение 1, если блок бракуется по герметичности, и х= 0, если блок исправный; у — случайную величину, равную 1 или 0 в зависимости от того, бракуется блок по выходным параметрам или нет. Тогда P(х = 0, у = 0) = 0,95 по условию, так как по условию задачи P(х = 0) = 1 - 0,03 = 0,97; Р (х = 0, у = 1) = P(х=0) - P(х = 0, у = 0) = 0,97 - 0,95 = 0,02. Аналогично, P(х = 1, у = 0) = 0,005, так как Р(х = 0) = 1 - 0,045 = 0,955; P(х = 0) = P(х = 0, у = 0) + P(х=1, у = 0). Отсюда Р(х=1, у = 0) = 0,955 - 0,95 = 0,005 и P(х=1, у=1) = P(х=0,у = l) + P(х= l, у = 0) = 0,02 + +0,005 = 0,025. Таким образом, совместное распределение (х, у) задается таблицей:
| у | х | ||
| 0,025 | 0,02 | ||
| 0,005 | 0,95 |
Откуда М {х}= 0,03; M{х2} = 0,03, σ2{х}= 0,029, M {у} = 0,045; М {у2} = 0,045; σ2 {у} = 0,0043. Ковариация равна 0,025. Коэффициент корреляции 0,669.
127. Брак при производстве РЭА из-за несоответствия полосы пропускания заданной равен 6%, причем среди забракованной по этому признаку аппаратуры в 4% случаев коэффициент частотных искажений превышает заданную величину. Среди аппаратуры, в которой отсутствует брак по полосе пропускания, брак по частотным искажениям встречается в 1% случаев. Определить коэффициент корреляции между двумя дефектами и вероятность брака по коэффициенту частотных искажений во всей партии
Ответ. r = 0,0936: P = 0,01.
Дата добавления: 2016-03-15; просмотров: 3489;
