Функция одного случайного аргумента
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х и записывают Y=φ(Х). Если Х – дискретная случайная величина и функция Y=φ(Х) – монотонная, то 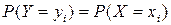 . Если φ(Х) – немонотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y, тогда вероятности возможных значений Х, при которых Y принимает одинаковые значения следует сложить.
. Если φ(Х) – немонотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y, тогда вероятности возможных значений Х, при которых Y принимает одинаковые значения следует сложить.
Если Х – непрерывная случайная величина с плотностью f(x), а y=φ(x) дифференцируемая строго возрастающая или строго убывающая функция, обратная для которой x=ψ(y) то плотность распределения g(y) случайной величины Y находят из равенства
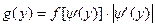
Если функция φ(x) не монотонна на интервале возможных значений Х, то этот интервал следует разбить на интервалы монотонности, найти плотность для каждого интервала, а затем результаты просуммировать.
Математическое ожидание функции Y=φ(Х) вычисляется по формулам:
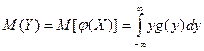 или
или 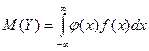 ,
,
а дисперсия –

Пример 1. Дискретная случайная величина задана законом распределения:
| xi | -1 | |||
| Pi | 0,1 | 0,3 | 0,4 | 0,2 |
Найти закон распределения случайной величины Y=X2, математическое ожидание M(Y), D(Y) и σ(Y).
Решение. Найдем возможные значения Y:
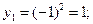
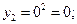


Найдем вероятности возможных значений
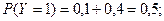
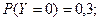
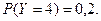
Следовательно, закон распределения величины Y имеет вид
| yi | |||
| Pi | 0,3 | 0,5 | 0,2 |
Тогда
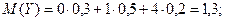

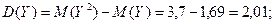
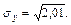
Пример 2. Случайная величина Х задана плотностью распределения f(x)=x+0,5 в интервале (0,1); вне этого интервала f(x)=0. Найти: а) плотность распределения функции Y=X2; б) математическое ожидание M(Y); в) дисперсию D(Y).
Решение. а) Так как функция y=x2 на промежутке (0,1) строго возрастает и имеет обратную  , то
, то
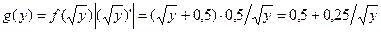
б) 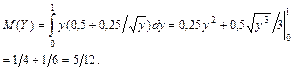
Математическое ожидание можно найти другим способом:
 .
.
в)  ,
, 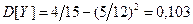 .
.
3. Случайная величина X задана плотностью распределения f(x)=cos(x) в интервале (0, π/2); вне этого интервала f(x)=0. Найти математическое ожидание функции Y=φ(X)=X2 (не находя предварительно плотности распределения Y).
4. Случайная величина X задана плотностью распределения f(x) =cos(x) в интервале (0, π/2); вне этого интервала f(x) =0. Найти дисперсию функции Y = φ(Х)=Х2, не находя предварительно плотности распределения Y. Для решения используем формулу
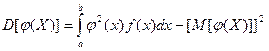
и то, что 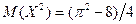 .
.
5. Дискретная случайная величина X задана законом распределения:
| Х | |||
| p | 0,2 | 0,1 | 0,7 |
Найти закон распределения случайной величины Y=2Х + 1.
6. Дискретная случайная величина X задана законом распределения:
| Х | π/4 | π/2 | 3π/4 |
| р | 0,2 | 0,7 | 0,1 |
Найти закон распределения случайной величины Y=sin(X).
7. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале (0,∞). Найти плотность распределения g(у) случайной величины Y, если: а) Y=e-х; б) Y=ln(X); в)Y=X2; г) Y=1/X2; д) Y=Х3 .
8. Случайная величина X распределена равномерно в интервале (0, π/2). Найти плотность распределения g(y)случайной величины Y=sin(X).
9. Случайная величина X распределена равномерно в интервале (-π/2, π/2). Найти плотность распределения g(y) случайной величины У=cos(X).
Дата добавления: 2016-03-15; просмотров: 5888;
