Последовательный колебательный контур.
Если последовательно с L и С включить генератор синусоидальной ЕДС, частота которого равна частоте свободных колебаний в контуре (резонансной частоте), то в контуре возникнут колебания. Но амплитуда их будет нарастать плавно, так как в момент включения в контуре возникают свободные колебания, фаза которых, противоположна фазе источника ЕДС. С течением времени свободные колебания затухают и в контуре нарастают вынужденные колебания.

Если бы в контуре не было потерь, то колебания нарастали бы до бесконечности. В реальном контуре колебания нарастают до тех пор, пока мощность источника не уравновесится мощностью потерь в контуре. При этом, чем меньше потери (Rn), тем дольше длятся свободные колебания, следовательно, тем медленнее нарастают вынужденные.
UL будет равно Uc, когда XL = Xc
Сопротивление L переменному току XL = oL
Сопротивление С переменному току ХC= - 1/ωС
Для L и С, определенных величин, можно определить такую частоту, (ω0) на которой XL = XС т. е. ωL = 1/ωC → ω2L = 1/C → ω2 = 1/LC → ω = = 1/(LC)1/2.
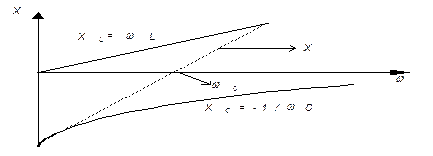
Это значит, что на резонансной частоте последовательного контура XL всегда равно ХС.
Входное сопротивление последовательного контура для источника ЕДС. Z = Rn + XL + Xc = Rn + ωL - 1/ωС = Rn +X
На резонансной частоте ω0:
X = XL – XС = ωL - 1/ωС = 0
Значит Z на резонансной частоте: Z0 = Rn.
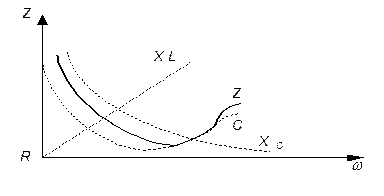
При отклонении от ω0 Z возрастает. Значит ток последовательного контура максимальный на резонансной частоте и уменьшается при отключении от ω0, I = E/Z.
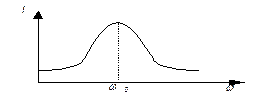
На резонансной частоте:
E = IRn; UL = IXL; UC = IXC, тогда UL/E = IXL/IRn = UC/E = IXC/IRn = = XC/Rn = XL/Rn = Q
Из этого следует, что при ХC = XL > Rn (XC > Rn) напряжение на С и L может быть в Q раз больше ЕДС источника сигнала:
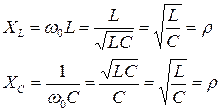
следовательно, на ω0 XL = XC = ρ ... = 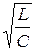 , когда Q = ρ/Rn.
, когда Q = ρ/Rn.
Если на последовательный контур подавать напряжение от внешнего генератора, а с конденсатора (или L) снимать выходное напряжение, то оно будет зависеть от частоты генератора.
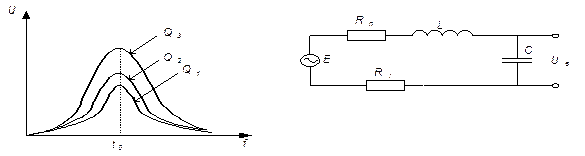
Ha f0 Uвых наибольшее: в Q раз больше чем Е. На частотах отличных от f0 ток уменьшается, следовательно Uвых тоже уменьшается.
Таким образом: последовательный колебательный контур обладает избирательным свойством, которое зависит от Q (Rn, ρ).
Для контуров с разными Q существует полоса частот, на которых уровень выходного сигнала ослабляется незначительно. Поэтому каждый контур обладает своей полосой пропускания.
Если принять допустимым уровень ослабления в 1,4 раза ( 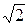 ), то существует математическое выражение для величины полосы пропускания.
), то существует математическое выражение для величины полосы пропускания.
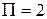 Δ
Δ 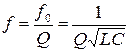

Последовательный контур можно применять для выделения сигналов определенных частот (например, в радиоприемниках). Недостатком его является то, что на его добротность (а следовательно и П) оказывает влияние Ri источника сигнала.
Для последовательного колебательного контура можно построить векторную диаграмму с учетом того, что в последовательной цепи ток протекающий во всех элементах один и тот же (напряжение С φ = 0).
В случае резонанса UL = UС, XL = ХС сумма трех векторов UL; UС; UR, равно U т.е. входному напряжению.
Если изменять частоту сигнала, то будут уменьшаться величины XL, XС, а их разность не будет ≠ 0.
Например, при увеличении частоты XL будет возрастать, а ХС спадать, следовательно, UL возрастает, a UC спадает. Из векторной диаграммы видно, что с ростом частоты напряжение тоже должно возрасти, то есть сопротивление возрастает, причем характер его становится индуктивным, так как φ между U и I положительное (как в L).
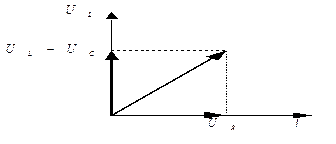
Дата добавления: 2016-03-15; просмотров: 1301;
