Статистические методы контроля качества продукции и услуг
В комплексной системе управления качеством продукции статистические методы контроля относятся к наиболее прогрессивным. Они основаны на применении методов математической статистики к систематическому контролю качества изделий и состояния технологического процесса с целью поддержания его устойчивости и обеспечения заданного уровня качества выпускаемой продукции.
Статистические методы контроля производства и качества продукции и услуг имеют следующие преимущества перед другими методами:
1) носят профилактический характер;
2) позволяют во многих случаях обоснованно перейти к выборочному контролю и тем самым снизить трудоемкость контрольных операций;
3) обеспечивают наглядность изображения динамики изменения качества продукции и настроенности процесса производства, что позволяет своевременно принимать меры к предупреждению брака не только контролерам, но и работникам цеха − рабочим, бригадирам, технологам, наладчикам, мастерам на стадии производства.
Статистические методы управления качеством продукции и услуг предполагают:
1) статистический анализ точности выполнения технологического процесса с целью приведения его к требуемой настроенности, точности и статистически устойчивому состоянию;
2) текущий контроль с целью регулирования и поддержания процесса в состоянии, обеспечивающем заданные качественные параметры;
3) выборочный статистический приемочный контроль качества готовой продукции.
Статистический анализ точности выполнения технологических процессов представляет собой единовременное обследование надежности процесса путем изучения качественных характеристик большого числа изделий, обработанных в определенных условиях на данной операции. Этот вид анализа дает возможность определить фактическую точность процесса и сравнить ее с заданной, оценить качество и устойчивость настроенности процесса, выявить вероятный процент дефектов, определить экономически целесообразные допуски.
Наиболее распространенными методами статистического анализа точности технологических процессов являются:
· сравнение средних значений параметров с номинальными;
· сравнение дисперсий;
· оценка коэффициентов корреляции;
· регрессионный анализ и др.
Метод сравнения средних значений параметров с номинальными используется в тех случаях, когда необходимо установить соответствие изготовляемого изделия эталону и в других случаях при сравнении значений одноименных показателей качества у нескольких групп изделий.
Метод сравнения дисперсий используется в случаях, когда требуется сделатьхарактеристику изменчивости показателей качества, их рассеивание в зависимости от способа обработки или других факторов.
Коэффициент корреляции используется при оценке степени зависимости показателей качества от других показателей.
К регрессионному анализу прибегают в случаях оценки показателя качества по результатам наблюдений за другими показателями.
Статистическое регулирование технологического процесса представляет собой корректировку значений параметров технологического процесса по результатам выборочного контроля параметров выпускаемой продукции с целью обеспечения требуемого уровня качества. В процессе статистического регулирования технологического процесса периодически проверяют небольшое количество (5–10 единиц) изготовляемой продукции на конкретной операции, рассчитывают соответствующий распределению статистический параметр качества и сопоставляют с его номинальным значением. Этот контроль обеспечивает непрерывное наблюдение за стабильностью операции, однородностью качества, что дает возможность своевременно сигнализировать о наступающем отклонении и тем самым предупреждать возникновение дефектов и брака, обеспечивая заданный уровень качества продукции.
Распределение качественного параметра можно представить в виде кривой нормального распределения (рисунок 1), подчиненной закону нормального распределения случайных величин:
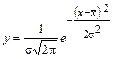, (1)
где y – плотность вероятностей или частота появления случайной переменной;
х – значение случайной переменной;
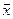– центр распределения (группирование) отклонений, при котором значение у наибольшее;
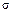– среднеквадратическое отклонение случайной переменной х.
|
|
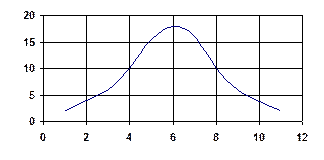
Рисунок 1– Кривая нормального распределения случайных величин
Приведем наиболее важные статистические характеристики закона нормального распределения:
1) среднее арифметическое значение качественного признака, характеризующее точность процесса,
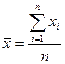, (2)
где п − количество единиц изделий в выборке (число замеров);
хi − замер контролируемого параметра i-го изделия в выборке;
2) среднеквадратическое отклонение случайной величины (значение качественного параметра, характеризующее величину поля фактического рассеивания размеров контролируемого параметра),
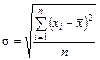; (3)
3) размах рассеивания качественной характеристики R,который представляет собой разность между наибольшими и наименьшими фактическими размерами,
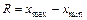. (4)
Результаты контроля (расчет приведенных характеристик) изображаются графически на карте статистического контроля (рисунок 2). Исходя из полученных параметров осуществляется управление процессом и принимаются решения о качестве продукции, выпущенной за период между двумя выборками.
| Количество выборок | ||||||||||||
| Контрольные параметры | Зона брака | |||||||||||
| R | 2,75 | 3,25 | 2,25 | 3,25 | 2,75 | 2,75 | 2,25 | 2,25 | ||||
| С = 4,2 | TBR | |||||||||||
 C = 3,864
| PBR 4 | δ’=4,2 | ||||||||||
| C = 0,479 | PHR 1 | |||||||||||
| C = 0 | THR |
Рисунок 2– Карта статистического контроля качества конденсаторов
Контрольная карта предназначена для статистического контроля по одному показателю качества. В ее верхней части отмечаются точками значения средних арифметических показателей качества х. Здесь нанесены четыре границы: две внешние, ограничивающие поле допуска, − Тв(верхний технический допуск) и Тн(нижний технический допуск), за пределами которых находится зона брака, и две внутренние − Рв(верхний предупредительный допуск) и Рн(нижний предупредительный допуск), между которыми находится номинальный размер контролируемого параметра Рном.
Внешние границы Тви Тнопределяются исходя из допустимой относительной величины отклонения контролируемого параметра от номинальной величины:
Тв = хном + ∆хф; (5)
Тн = хном − ∆хф, (6)
где ±∆хф− допустимая абсолютная величина отклонения от номинального размера,
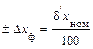, (7)
где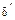 
– допустимая величина отклонения от номинальной величины, %.
Внутренние границы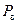 
и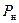 
определяются по формулам:
; 
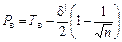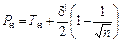, (8)
где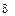 
– поле допуска на величину изучаемого параметра (по нижнему и
верхнему пределам от номинала);
п – количество единиц изделия в выборке.
Среднеарифметическая величина изучаемого параметра в j-й выборке
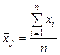, (9)
где хi – значение контролируемого параметра i-го изучения в j-й выборке.
Положение контрольных линий регулирования размахов РвR и РнR определяется по формулам:
РвR = V1d; (10)
РнR = V2d, (11)
где Vi и V2 принимаются по таблицам, составленным на основе корреляционного анализа измеряемого параметра.
Ниже помещаются результаты замеров выборки (5−10 изделий) и среднее арифметическое значение по каждой выборке х. В нижней части карты по каждому номеру выборки откладываются значения размаха варьирования и наносится нижняя сплошная граница (обычно ТнR принимается равной нулю, а ТвR − равной полю допуска), верхняя граница регулирования размахов РвR (ограничивающая зону допускаемых значений размахов R в выборках), а также сплошная линия TвR (верхний предел допуска).
Технологический процесс протекает удовлетворительно, если средние арифметические значения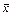 
выборок не выходят за границы регулирования Рви Рн, а размахи R не выходят за свою границу TвR. В этом случае вся партия, подготовленная между текущей и предыдущей выборками, считается годной и убирается с рабочего места. Если же в выборке обнаружен брак или статистический анализ указывает на возможность его появления при данном состоянии технологического процесса, вся накопившаяся у станка за последний период времени продукция подлежит разбраковке, а станок останавливается для переналадки.
Предупредительные границы Рви Рн устанавливаются таким образом, чтобы выход тех или иных значений за предел этих границ под влиянием погрешностей, нарушающих нормальный ход процесса, еще не означал появление брака, а лишь предварительно сигнализировал о возможности его возникновения, если эти погрешности не будут немедленно устранены. В подобных случаях контролер, отмечая на карте полученные значения и сопоставляя их с положением границ регулирования, должен предупредить администрацию участка или цеха о возможности появления брака и о необходимости произвести подналадку оборудования.
Из приведенного примера видно, что в период между первой и третьей выборками наблюдалась систематическая расстройка оборудования. В результате на третьей выборке было обнаружено, что величина х превысила допустимое значение Рв. Процесс был остановлен, что отмечено на карточке знаком (↓), и оборудование было перенастроено. Детали, изготовленные между второй и третьей выборками, подверглись сплошному контролю.
После возобновления процесс пошел в пределах установленных границ, однако в восьмой выборке было обнаружено, что размах R превысил допустимое значение ТвR. Оборудование было вновь остановлено (↓). Детали, изготовленные между седьмой и восьмой выборками, подвергались сплошному контролю. После выявления и устранения случайных факторов, ухудшающих качество продукции, процесс был возобновлен и до одиннадцатой выборки включительно протекал в пределах предупредительных границ.
Точность настройки процесса
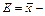хср; (12)
хср = (хmах – хmin)/2, (13)
где 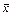– среднеарифметическая величина параметра для всех выборок;
хmaxи хmin− наибольшая и наименьшая величина параметра из всех выборок;
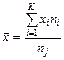, (14)
где К – число выборок;
ni – общее число измеряемых изделий, шт.;
nj – число деталей в j-й выборке, шт.
Коэффициент точности настройки производственного процесса (фактический)
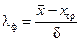. (15)
Коэффициент точности расчетный
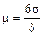. (16)
При μ = 1 точность процесса считается удовлетворительной, при μ < 1 − хорошей, при μ > 1 − неудовлетворительной.
Допустимый коэффициент точности настройки процесса
lд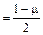 
. (17)
По результатам расчетов (15) – (17) делается вывод: если lф < lд, то настройка процесса хорошая, если lф > lд − неудовлетворительная.
Статистический приемочный контроль изделий используется в качестве выборочного метода при приемке больших партий продукции, сырья, материалов, полуфабрикатов. Он основан на применении методов математической статистики для проверки соответствия качества продукции установленным стандартом. По качеству выборки, взятой на контроль, с достаточной достоверностью делают оценку качества всей партии.
Преимущества приемочного статистического контроля состоят в сокращении трудоемкости контроля по сравнению со 100 %-й проверкой продукции, гарантированном обеспечении заданного качества продукции, достоверности оценки заданного уровня качества.
При статистическом приемочном контроле могут быть использованы два метода:
1) контроль по альтернативному признаку, когда за показатель качества принимается доля брака в выборке;
2) контроль по количественному признаку, когда определяются статистические характеристики распределения измеряемого параметра в выборке (среднее значение 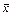и дисперсия σ), и по полученным значениям оценивается качество всей партии изделий.
При приемочном контроле по количественному признаку определяются фактические значения измеряемого параметра у всех изделий в выборке, средние арифметические значения этих параметров х и дисперсия d, после чего решаются неравенства (15) – (17).
Если все неравенства оказываются верными, партия принимается. В противном случае партия идет на разбраковку. Преимуществом этого метода является значительно меньший объем выборки при той же достоверности оценки партии (объем выборки сокращается в 3−10 раз), что особенно важно при контроле, который связан с разрушением изделий.
Дата добавления: 2016-03-10; просмотров: 3505;