Понятие корреляционного и регрессионного анализа

Различают функциональные и стохастические (вероятностные) взаимосвязи между признаками.

Функциональная связь – жесткая обратимая зависимость, когда каждому изменению факторного признака (независимого) соответствует строго определенное изменение результативного, т.е. зависимого признака. Например, заработная плата рабочего сдельщика прямо пропорциональна выполненному объему. Из этой зависимости можно определить расценку или объем произведенной продукции.

Если изменение факторного признака или комбинации признаков приводит к вариации значений результативного, то говорят о наличии стохастической или корреляционной (частного случая) связи. Этот вид взаимосвязи нежесткий, необратимый.

Корреляционная связь – частный случай стохастической связи, при этом среднее изменение факторного признака приводит к изменению среднего значения результативного признака. Например, с ростом стажа, как правило, растет средняя заработная плата. С увеличением вносимых удобрений, как правило, растет урожайность. Если с ростом факторного признака растет среднее значение результативного – связь прямая, если уменьшается – связь обратная.

Если рассматривать влияние только одного факторного признака, имеют место парные корреляции.

Если исследуется влияние нескольких факторных признаков на результативные, говорят о множественной, многофакторной корреляции.

Для исследования функциональной зависимости используется балансовый и индексный метод.

Для исследования корреляционной связи используют группу методов для изучения качественных признаков и количественных. Связь количественных признаков изучается параметрическими методами (параллельных рядов; графическим; аналитических группировок; корреляционно-регрессионным анализом), а качественных – с помощью непараметрических методов на основе таблиц сопряженности.[4] Наиболее точным и детальным является корреляционно-регрессионный анализ (КРА).

Задачей корреляционного анализа является определение тесноты связей. Цель регрессионного анализа - определение вида и параметров уравнения теоретической кривой. Недостатками корреляционно – регрессионного анализа является необходимость обработки большого массива сопоставимых данных. Выводы, полученные на основе КРА, можно использовать только для данных, сопоставимых с исходными, на основе которых проводился КРА.

Парная регрессия

Парная регрессия отражает связь между двумя признаками – результативным и факторным. Аналитически эту связь можно представить уравнениями

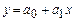- прямая,

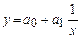- гипербола,

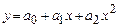- парабола.

Для того чтобы определить, какая это связь, необходимо изучить само явление, то есть выявить: возможно ли монотонное возрастание или убывание функции, нет ли точек насыщения, перегиба, асимптот. После выбора возможного типа теоретической кривой определяются ее параметры с помощью метода наименьших квадратов «МНК»

Параметры выбранного типа теоретической кривой подбираются, исходя из условия, что сумма квадратов отклонений фактических значений результативного признака от теоретических будет минимальной. .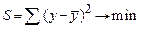

С этой целью на основе решения системы нормальных уравнений, определенных для каждого вида теоретической кривой, рассчитываются коэффициенты регрессии. Например, для линейной парной регрессии у=а₀+а₁х система нормальных уравнений имеет вид

,

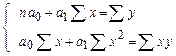где х и y – данные наблюдения.

Решение этой системы относительно а₀ и а₁ позволит определить коэффициенты регрессии в уравнении регрессии и составить уравнение теоретической кривой. Коэффициент при x показывает, на сколько своих единиц измерения изменяется результативный признак при изменении факторного признака на свою единицу измерения. Свободный член уравнения характеризует влияние всех прочих факторов кроме x.

Пример 6.1

Составить уравнение регрессии по данным таблицы 14.

Таблица 14

№ п/п	Прибыль у, тыс. руб.	Затраты на 1 руб. х, руб.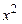
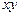
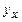
	1200,00	0,96	0,92	1152,00	1869,19
	2400,00	0,77	0,59	1848,00	1873,00
	2480,00	0,77	0,59	1909,60	1873,00
	1600,00	0,89	0,79	1424,00	1870,60
	1750,00	0,82	0,67	1435,00	1872,00
	1800,00	0,81	0,66	1458,00	1872,20
Итого:	11230,00	5,02	4,23	9226,60	11230,00

Решение

,

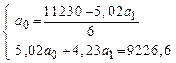
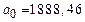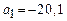
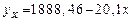
На основе уравнения регрессии можно сделать вывод, что с ростом затрат на единицу продукции на 1 рубль прибыль предприятия снижается на 20,1 тыс. руб.

 

<11121314151617>

---

Дата добавления: 2016-03-05; просмотров: 760;

---