Характеристика выборочного наблюдения
Выборочное наблюдение представляет собой один из методов не сплошного наблюдения, характеризуется тем, что отобранная в случайном порядке часть единиц дает представление о всей изучаемой совокупности по какому-либо признаку.
При проведении выборочного наблюдения необходимо обеспечить случайность выборки и её репрезентативность (представительность).
Принцип случайности означает, что все единицы совокупности должны иметь равные шансы попасть в выборку.
Для обеспечения принципа репрезентативности необходимо, чтобы выборка была достаточной. В этом случае ошибка выборки не превысит допустимые размеры.
Преимущества выборочного наблюдения:
1. Экономия времени, материальных и денежных ресурсов.
2. Возможность проведения там, где невозможно проведение сплошного наблюдения (например, при проверке качества продукции, связанного с её уничтожением – вскрытие консервов, проверка лампочек).
Недостатки выборочного наблюдения:
- возникновение ошибок выборки.
Совокупность, из которой осуществляется выборка, называется генеральной. Отобранная часть представляет выборочную совокупность или выборку.
Ошибками выборки называются расхождения между характеристиками генеральной и выборочной совокупностей. Причина появления ошибок выборки – отличие структуры выборки от структуры генеральной совокупности.
Для определения и обозначения основных характеристик генеральной и выборочной совокупностей используют следующие условные обозначения (табл.15):
Таблица 15
Условные обозначения основных характеристик
генеральной и выборочной совокупностей
| Показатели | Генеральная совокупность | Выборочная совокупность |
| Численность выборки | 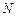
| 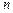
|
| Среднее значение признака | 
| 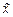
|
| Общая дисперсия | 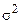
| 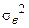
|
| Межгрупповая дисперсия | 
| 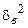
|
| Доля единиц, обладающих признаком | 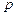
| 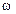
|
| Доля единиц, не обладающих признаком | 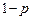
| 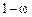
|
| Частота | 
| 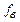
|
Ошибки выборки
Различают два вида ошибок выборки:
- стандартная или средняя;
- предельная
Под средней ошибкой выборки понимают такое расхождение между средней генеральной совокупности и средней выборочной совокупности, которое не превышает  (среднего квадратического отклонения).
(среднего квадратического отклонения).
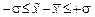
Предельной ошибкой выборки считают максимально возможное расхождение между средней генеральной и средней выборочной совокупности при заданной вероятности её появления.
В основе определения ошибок выборки лежит закон нормального распределения. Формула средней ошибки выборки зависит от метода (способа) проведения выборочного наблюдения (собственно случайный отбор, серийный , механический отбор),объема выборки и вариации признака.
Для собственно случайного повторного отбора стандартная или средняя ошибка выборки определяется по формуле:
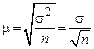 ,
,
где n – численность выборки.
Для собственно случайного бесповторного отбора ошибка выборки определяется по формуле: 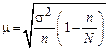 .
.
Организовать собственно случайный повторный отбор сложнее собственно случайного бесповторного отбора, т.к. рассчитывать ошибку легче по формуле случайного повторного отбора, а организовывать выборку удобнее как случайную бесповторную, тона практике используют случайный бесповторный отбор, а ошибку выборки рассчитывают как при повторном отборе, несколько завышая её величину.
где t – коэффициент доверия, который определяется по таблице нормального распределения.
Предельная ошибка выборки используется при определении доверительного интервала, который выглядит так:
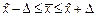 .
.
Чем выше вероятность, с которой гарантируется попадание в доверительный интервал, тем больше величина доверительного интервала.
Наряду с абсолютной величиной рассчитывается относительная величина ошибки выборки,которая в общем случае определяется по формуле 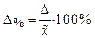 .Для альтернативного признакаошибки определяется по следующим формулам:
.Для альтернативного признакаошибки определяется по следующим формулам: 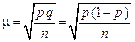
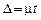 ,
,
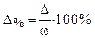 .
.
В статистике доказано, что общая величина дисперсии генеральной совокупности связана с дисперсией выборки следующим соотношением:  .
.
При большом объеме выборки (  )
) 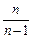 стремится к 1 и
стремится к 1 и  , поэтому среднюю ошибку выборки можно рассчитывать на основании выборочной дисперсии по формуле
, поэтому среднюю ошибку выборки можно рассчитывать на основании выборочной дисперсии по формуле 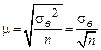
Пример 7.1
При проверке веса импортируемого груза на таможню методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4г. С вероятностью 99,7% определить доверительный интервал в котором находится средний вес изделия всего импортируемого груза.
Решение:σ=4, V=200 , 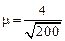 ,
,  .
.
Определим интервал, в котором находится средний вес по всему грузу: 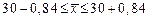
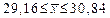
Ответ: с вероятностью 99,7% можно гарантировать, что вес изделия импортируемого груза будет находиться в интервале от 29,16 г. до 30,84 г.
Дата добавления: 2016-03-05; просмотров: 1936;
