Определение необходимой численности выборки. Необходимый объем выборки можно вывести исходя из формул предельная и средней ошибок выборки:
Необходимый объем выборки можно вывести исходя из формул предельная и средней ошибок выборки:
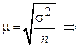
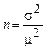 ,
, 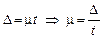 , отсюда
, отсюда 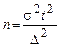 , где n – необходимая численность выборки.
, где n – необходимая численность выборки.
Необходимая численность выборки n прямо пропорциональна вариации признака, вероятности, с которой гарантируется результат, и обратно пропорциональна предельной ошибке выборки.
Таким образом, для определения необходимого объема выборки следует заранее знать как вероятность, так и дисперсию. Но последнюю характеристику можно рассчитать только по результатам выборочного наблюдения. Получается замкнутый круг, когда объем выборки нельзя рассчитать без дисперсии и наоборот. Чтобы решить эту проблему, предварительно проводят пробные наблюдения. Полученные результаты по выборочной дисперсии используют для расчета необходимой численности выборки. При этом дисперсию стараются несколько завысить. Чем выше σ2, тем больше объем выборки, следовательно, уменьшается ошибка выборки.
Численность выборкиальтернативного признака определяется на основе формул:
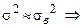
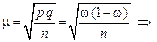
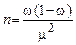 ,
, 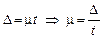 , отсюда
, отсюда 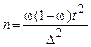 ,
,
где 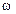 – доля единиц выборки, обладающих данным признаком;
– доля единиц выборки, обладающих данным признаком; 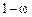 – доля единиц выборки, не обладающих данным признаком.
– доля единиц выборки, не обладающих данным признаком.
Для альтернативного признака используют максимальную величину дисперсии. Известно, что произведение 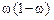 будет максимально при
будет максимально при 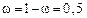 , тогда формула для определения численности выборки будет следующей:
, тогда формула для определения численности выборки будет следующей: 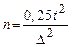 .
.
Для каждого метода выборочного наблюдения (собственно случайный отбор, серийный отбор, механическая или типологическая выборка) необходимый объем выборки рассчитывается на основе своей формулы ошибки выборки.[5]
Малая выборка
В ряде случаев, связанных с проверкой качества продукции, проведением таможенного контроля и др., невозможно проводить отбор единиц в большом объеме, поэтому используют малую выборку, т.е. выборку с объемом, не превышающим 30 единиц. В этом случае необходимо учитывать влияние коэффициента 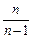 . Поэтому
. Поэтому 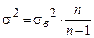 , соответственно, средняя ошибка малой выборки рассчитывается по формуле:
, соответственно, средняя ошибка малой выборки рассчитывается по формуле:
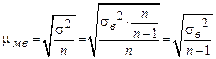
Предельную ошибку малой выборки определяют по формуле:
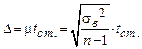 ,
,
где 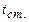 – коэффициент Стьюдента.
– коэффициент Стьюдента.
Если объем выборки больше или равен 30 единиц, то вероятность ошибок выборки подчинена закону нормального распределения. Для малой выборки вероятность ошибок выборки определяется по закону распределения Стьюдента (см. таблицу 16).
Таблица 16
Вероятность распределения ошибок по закону нормального распределения и распределению Стьюдента
| t | По закону Стьюдента | По закону нормального распределения |
| 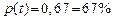
| 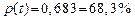
|
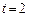
| 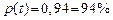
| 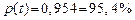
|
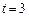
| 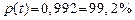
| 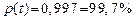
|
Контрольные вопросы к теме 7
1. Приведите определение выборочного наблюдения.
2. Какие методы организации выборочного наблюдения Вы знаете?
3. Назовите виды ошибок выборки.
4. Какая выборка называется малой выборкой?
5. От каких факторов зависит объем необходимой численности выборки?
6. Как решить проблему взаимосвязи расчета дисперсии и необходимого объема выборки?
РЯДЫ ДИНАМИКИ

• Виды рядов динамики и их характеристика • Условия
сопоставимости рядов динамики • Расчет среднего уровня ряда
динамики • Показатели рядов динамики• Смыкание рядов динамики
Дата добавления: 2016-03-05; просмотров: 985;
