Нормальное распределение и его характеристики

Анализ эмпирических частот вариационного ряда позволяет выявить тип распределения, подобрать теоретическую кривую, определить ее параметры и проверить правильность гипотезы о типе распределения данного ряда. Характер кривой лучше выявляется при большом объеме наблюдений и малых интервалах

Большое значение имеет сопоставление фактических кривых с теоретическими. Наиболее часто в качестве теоретической кривой используют кривую нормального распределения(рис. 5), плотность распределения которой выражается уравнением:

,

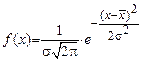где f(x) – ордината кривой нормального распределения (частость); t – нормированное отклонение 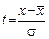; π =3,14 , .

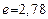Характеристики кривой нормального распределения:

- кривая симметрична и имеет максимум 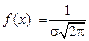в точке ;

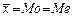- кривая асимптотически стремится к оси абсцисс

- кривая имеет две точки перегиба на расстоянии 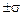от ;

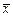- при 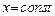с ростом σ кривая становится более пологой (рис. 5);

- при 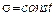с изменением средней кривая не меняет своей формы, а лишь сдвигается вправо или влево по оси x (рис. 5);

- в интервале 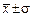находится 68,3% всех единиц совокупности, в интервале 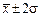– 95,4%, в интервале 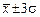– 99,7% (практически все значения);

-коэффициенты эксцесса и асимметрии равны нулю.

Рис. 5. Кривые нормального распределения