Справочник простейших функций для заданий
| Уравнения прямой | ||
| Прямая параллельна оси Х, пересекает ось Y в точке (0,b). | y=b | |
| Прямая параллельна оси Y, пересекает ось X в точке (a,0). | x=a | |
| Прямая проходит через точку (x1,y1) под углом aк оси Х. | (y-y1) = k(x-x1) | k = tg a
0 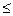 a<p
a a<p
a 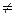 p/2 p/2
|
| Прямая пересекает ось Y в точке (0,b) под углом a к оси Х. | y = kx+b | |
| Прямая проходит через (0,0) под углом a к оси Х. | y = kx | |
| Прямая проходит через две точки (x1,y1)и (x2,y2), где x1≠x2, y1≠y2. | 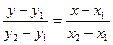
| |
| Прямая пересекает ось Х в точке (a,0), ось Y в точке (0,b) (уравнение прямой в отрезках). | 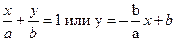
| |
| Длина отрезка, соединяющего две точки (x1,y1)и (x2,y2) | 
| |
| Уравнения окружности | ||
| Уравнение окружности радиуса R с центром (x0,y0). | (x-x0)2 + (y-y0)2 = R2 | |
Параметрические уравнения окружности радиуса R с центром в точке (x0,y0). Аргумент α: 0 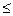 a<2p a<2p
| 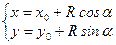
| |
| Уравнения эллипса, оси которого совпадают с осями координат | ||
| Каноническое уравнение эллипса с длинами полуосей а и b и центром в точке (x0,y0). | 
| |
Параметрические уравнения эллипса с длинами полуосей а и b и центром в точке (x0,y0) 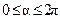
| 
| |
| Уравнения параболы | ||
| Уравнение параболы, ось которой параллельна оси Х, а вершина – в точке (x0,y0). | x =± (y – y0)2 + x0 | |
| Уравнение параболы, ось которой параллельна оси Y, а вершина – в точке (x0,y0). | y = ± (x – x0)2 + y0 |
Дата добавления: 2016-02-13; просмотров: 728;
