НЕПРЕРЫВНОЕ НАЧИСЛЕНИЕ ПРОЦЕНТОВ
В зависимости от частоты начисления процентов наращение суммы осуществляется различными темпами, причем с возрастанием частоты накопленная сумма увеличивается. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала. Из формулы (4.7) следует:
lim (1 +r/m) k · m = е r · k при m à ∞,
так как lim (1 + 1/m)m = епри mà +∞,
где е — одна из важнейших постоянных математического анализа, относящаяся к группе так называемых замечательных пределов; трансцендентное число е = 2,718281... широко используется в элементарной математике (при построении логарифмических и показательных функций), а также в теории вероятностей и математической статистике (при построении функций распределения).
Таким образом, при непрерывном начислении процентов в пределах одного года используется следующая базовая формула:
F1 = Р · е r(4.12)
Пример
Рассчитать накопленную сумму для различных вариантов начисления процентов за один год, если исходная сумма Р = 1000 руб. и r = 10%.
| Р | Частота начисления | Fn | Наращение | |
| Базисное | цепное | |||
| Ежегодное (m = 1) Полугодовое (m = 2) Квартальное (m = 4) Ежемесячное (m = 12) Ежедневное (m = 365) Непрерывное (m = ∞) | 1100,00 1102,50 1103,81 1104,71 1105,16 1105,17 | –– +2,50 +3,81 +4,71 +5,16 +5,17 | –– +2,50 +1,31 +0,90 +0,45 +0,01 |
Приведенные расчеты подтверждают наличие прямой зависимости между частотой начисления процентов и накопленной суммой; последняя графа таблицы показывает, что с увеличением частоты начисления темп прироста накопленной суммы уменьшается.
Графически изменение накапливаемой суммы в зависимости от частоты начисления имеет следующий вид (рис. 4.4).
Ежегодное Полугодовое Непрерывное
начисление начисление начисление 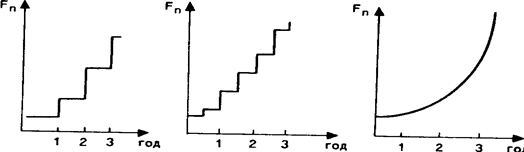
| Рис. 4.4. Различные варианты начисления процентов |
Сравнительная характеристика и интерпретация приведенных графиков достаточно очевидны, вместе с тем эти графики позволяют наглядно представить влияние частоты начисления процентов. При дискретном наращении каждая «ступенька» характеризует прирост основной суммы в результате очередного начисления, причем величина «ступеньки» все время возрастает. В рамках одного года одной «ступеньке» на левом графике соответствуют две «ступеньки» на среднем графике меньшего размера, однако в сумме они превышают первую «ступеньку» однократного начисления. Таким образом, ордината точки, соответствующей концу трехлетнего периода, на среднем графике будет выше, чем на левом. Еще более быстрым темпом идет наращение при непрерывном начислении, что и показывает график справа.
Дата добавления: 2016-03-04; просмотров: 1229;
