Дисконтирование и удержание процентов

Дисконтирование и удержание процентов является, по сути, обратными операциями по отношению к начислению процентов. Различают математическое дисконтирование и банковский учет.

Математическое дисконтирование позволяет узнать какую исходную сумму 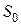нужно вложить, чтобы получить по истечении определенного времени, например, n-лет наращенную сумму 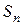при наращении по годовой процентной ставке i.

1) В случае простых процентов из формулы (1.2) следует

(1.13)

или из формулы (1.4) можно определить

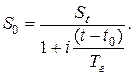
2) В случае сложных процентов из формулы (1.6) следует

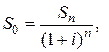(1.14)

или из формулы (1.7) можно определить

при m-кратном начислении процентов математическое дисконтирование определяется формулой

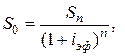(1.15)

где 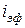определяется формулой (1.11).

Величина 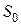называется приведенным значением величины 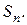При математическом дисконтировании годовые процентные ставки i называются ставками дисконтирования.

Банковский учет – это покупка банком денежных обязательств (денежных эквивалентов) по цене меньшей номинальной, указанной в обязательствах суммы.

Примером денежных обязательств может служить вексель - долговая расписка, содержащая обязательство выплатить определенную денежную сумму (номинал, указанный в векселе) в определенный срок.

В случае покупки банком векселя говорят, что он учитывается банком по номинальной сумме 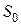, а клиенту выплачивается сумма

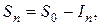(1.16)

где 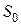- номинальная сумма векселя;

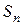- цена покупки банком векселя за n-лет до срока его погашения;

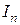- дисконт или доход банка.

Формулу (1.16) можно записать в виде:

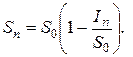
При n равном одному году отношение 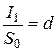называют годовой учетной ставкой денежных обязательств или банковской ставкой дисконтирования.

Учет денежных обязательств может осуществляться банком по простой и сложной схеме дисконтирования.

В случае простой схемы дисконтирования последовательность сумм, которые могут быть выплачены клиенту при увеличении n образуют убывающую арифметическую прогрессию с общим членом

(1.17)

равным сумме, которую получит клиент от банка за n-лет до погашения денежного обязательства.

В случае сложной схемы последовательность сумм, которые могут быть выплачены при увеличении n образуют геометрическую убывающую прогрессию со знаменателем и общим членом

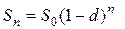(1.18)

равным сумме, которую получит клиент от банка за n-лет до срока погашения денежного обязательства.

При сроке до погашения денежного обязательства не кратному одному году формулы дисконтирования по простой и сложной схеме можно записать в виде:

(1.19)

где t – количество дней до срока погашения денежного обязательства;

Т_г – количество дней в году.

Расчеты, проведенные по формулам (1.19) позволяют сделать следующие выводы:

1) Зависимость 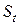от t при простой схеме дисконтирования является линейной спадающей функцией (см. рис. 1.3). При 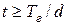клиенту не имеет смысла закладывать денежные обязательства, так как выплачиваемая ему банком сумма будет равна нулю.

2) Зависимость 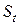от t при сложной схеме банковского дисконтирования является показательной при основании показательной функции (см. рис. 1.4).

Рис. 1.4. Дисконтирование по простой и сложной ставкам

3) Сумма, выплачиваемая клиенту при сроке n = 1 год до погашения денежного обязательства при его учете по простой и сложной схеме одинаковы.

4) При сроке учета t меньше одного года банку выгоднее учитывать денежное обязательство по сложной ставке дисконтирования, а при сроке учета больше года – по простой учетной ставке.