Дисконтирование. Расчет первоначальной стоимости

В практике финансовых расчетов может возникнуть и обратная по отношению к наращению задача: по известной наращенной сумме (S) определить размер размещенных средств (P), что наглядно представлено на рис. 2

P = ?

d

S время

Рис. 2. Дисконтирование с течением времени

Вычисление S на основе P называется дисконтированием. Таким образом, исчисление первоначальной стоимости связано с дисконтированием наращенной стоимости (ее уменьшением).

Дисконт (d) – это скидка (в процентах), определяемая по отношению к наращенной (будущей) стоимости для получения исходной величины, называемой первоначальной суммой.

Дисконтирование – действие, противоположное начислению процентов.

К дисконтированию обращаются, прежде всего, в практике торговой, инвестиционной и банковской деятельности.

Сумму дисконта (D) можно рассчитать по формуле

D = S – P . (11)

В финансовой практике используются два метода дисконтирования: метод математического дисконтирования и метод банковского (коммерческого) учета.

К математическому дисконтированию прибегают в тех случаях, когда по известной наращенной сумме (S), процентной ставке (i) и времени обращения (t) необходимо найти первоначальную стоимость (P). При этом предполагается, что проценты начисляются на первоначальную, а не наращенную сумму денег.

Дисконт, как и саму первоначальную сумму, можно находить по схеме простых и сложных процентов.

Первоначальную сумму при простом математическом дисконтировании можно рассчитать по формуле

P= 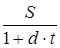, (12)

где – дисконтный множитель.

Пример 14

Через 6 месяцев с момента выдачи ссуды заемщик уплатил кредитору 21 400 руб. Кредит предоставлялся под 14 % годовых. Определить сумму кредита и сумму дисконта.

Решение

P = 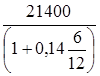= 20 000, руб.;

D = 21 400 – 20 000 = 1 400, руб.

Для математического дисконтирования по сложным процентам используется формула

P= 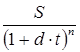, (13)

где d – ставка дисконта, выраженная в коэффициенте.

Пример 15

Определить первоначальную величину банковского вклада, если ее будущая стоимость через 2 года составит 23 328 руб. Сложная процентная ставка – 8 % годовых.

Решение

Р = 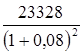= 20 000, руб.;

D = 23 328 – 20 000 = 3 328, руб.

На практике математическое дисконтирование используется для определения суммы капитала, необходимого для инвестирования под определенные проценты для получения требуемой величины денежных средств, а также в случаях начисления процентов, удерживаемых вперед при выдаче ссуды.

Наиболее распространенным методом дисконтирования является банковское дисконтирование (коммерческий учет).

Эта процедура представляет собой действие, обратное математическому дисконтированию. Отличие банковского дисконтирования от математического состоит в том, что в случае коммерческого учета ставкой выступает дисконт (d), а при математическом дисконтировании ставкой является обычная процентная ставка (i).

Таким образом, в случаях операций банковского дисконтирования целесообразно воспользоваться следующими формулами:

S= P · (1 – d·t) (14)

или

P = 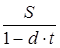. (15)

Соответственно, при инвестировании денежных средств соблюдается неравенство S > P, а в случаях дисконтирования, соответственно P > S или S < P, что раскрывает сущность вычисления наращенной, в первом примере, и первоначальной стоимости во втором.

На практике операции, связанные с дисконтированием денежных средств используются при финансовых операциях по учету векселей, выдачи дисконтных ссуд или перепродажи контрактов, в процессе уменьшения балансовой стоимости имущества (амортизации средств), первичного и вторичного размещения ценных бумаг и т. д.

Пример 16

Финансовая компания выдала ссуду 10 000 руб. на 2 года под простой дисконт, равный 9 % в год. Какую сумму получит клиент в момент получения ссуды?

Решение

S = 10 000 (1 – 0,09 · 2) = 8 200, руб.

Также как и в случае начисления процентов, срок обращения актива при дисконтировании может составлять менее года. В связи с этим, можно скорректировать ставку дисконта под заданный временной интервал в виде отношения 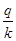, где q – число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k – число дней (месяцев, кварталов, полугодий и т. д.) в году.

В связи с этим, формула (14) изменяется и имеет следующий вид:

S = P (1 – d · ). (16)

Пример 17

Финансовая компания выдала ссуду 10 000 руб. на 180 дней под простой дисконт, равный 10 % в год. Какую сумму получит клиент в момент получения ссуды?

Решение

S = 10 000 (1 – 0,1· 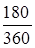) = 9 500, руб.

В случаях непрерывного дисконтирования или неоднократного учета векселей, ценных бумаг на одинаковых условиях в финансовых расчетах применяется сложная ставка дисконта:

S = P (1 – )^mn. (17)