Понятие о вырождении системы частиц

Система частиц называется вырожденной, если её свойства за счёт квантовых эффектов отличаются от свойств классических систем. Найдём критерии вырождения частиц. Распределения Ферми-Дирака и Бозе-Эйнштейна можно представить в следующем виде

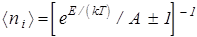, (6)

где А= 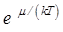- параметр вырождения. (7)

При А<<1 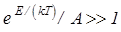и ±1 в (6) можно пренебречь. В итоге получаем

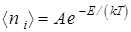(8)

Это распределение Максвелла-Больцмана для классических систем [см. формулу (34) в лекции 1,2]. Из анализа (7) следует, что чем выше температура Т, тем меньше А и тем более классическим становится распределение частиц по энергиям (8).

Температура, при которой начинают проявляться квантовые эффекты, называется температурой вырождения . Можно показать, что

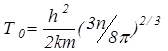, (9)

где m и n - масса и концентрация частиц.

Таким образом, при Т<<T₀ газ вырожден и подчиняется квантовым статистикам. При газ не вырожден и он подчиняется классической статистике Максвелла-Больцмана.

Расчёт по формуле (9) позволяет определить температуру вырождения:

1. Для водорода при нормальных условиях ( ) 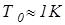, следовательно, водород при Т>>1K не вырожден и подчиняется классической статистике Максвелла-Больцмана.

2. Для свободных электронов (для электронного газа) в серебре 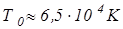. Подобные же значения получаются для всех других хорошо проводящих металлов. При таких высоких температурах ни один металл в твёрдом состоянии существовать не может. Отсюда следует, что электронный газ в металлах полностью вырожден и подчиняется только квантовой статистике Ферми-Дирака.

3. Для фотонов, масса которых равна нулю, из (9) следует, что 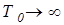. Следовательно, газ фотонов всегда вырожден и подчиняется квантовой статистике Бозе-Эйнштейна.