Фигура Земли. Потенциал силы тяжести

Потенциал силы тяжести ( 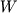) был введен в теорию гравиметрии для облегчения решения теоретических задач. В точке А, расположенной на расстоянии r_A от центра Земли, выражение для потенциала принимается равным: W_A=GM/r_A, а в любой точке B, расположенной на продолжении радиуса , 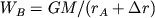. Поэтому разность потенциалов будет равна:

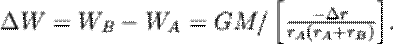
В пределе при малом 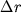имеем:

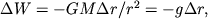
отсюда g=-dW/dr, т.е. сила тяжести есть производная потенциала силы тяжести по направлению к центру Земли.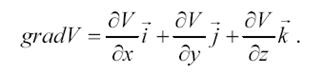

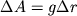С другой стороны, работа, которая может быть произведена при движении притягиваемой точки по отрезку , равна . Поэтому 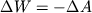, или работа силы тяжести по перемещению единичной массы на отрезке 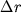равна разности значений потенциала на концах этого отрезка.

Потенциал силы притяжения обладает следующими свойствами

1. При перемещении точки в направлении, перпендикулярном действию силы, потенциал остается постоянным (уровенная или эквипотенциальная поверхность)

2. При перемещении массы по замкнутому контуру работа равна нулю

3. При перемещении точки вдоль действия силы f на расстояние dS приращение потенциала определяется, как произведение силы на расстояние: dV = f *dS (теорема Брунса)

4. Вне возмущающих масс действует уравнение Лапласа

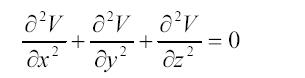
5. Внутри возмущающих масс действует уравнение Пуассона

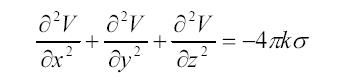
При перемещении точки в направлении, перпендикулярном силе тяжести, dW=0. Это означает, что W=const. Поэтому гравитационное поле можно представить в виде набора бесконечного числа поверхностей, на которых потенциал остается постоянным, а ускорение силы тяжести направлено перпендикулярно этой поверхности. Такие поверхности называют эквипотенциальными или уровенными. В частности, поверхность жидкости на Земле, например, моря, совпадает с уровенной поверхностью. У Земли есть одна уникальная уровенная поверхность, которая совпадает с невозмущенной волнениями поверхностью океанов. Она называется геоидом или фигурой Земли.

Таким образом, геоид - это условная уровенная поверхность, которая совпадает со средним уровнем океанов и открытых морей, проходит под сушей и по определению везде горизонтальна, а ускорение силы тяжести к ней перпендикулярно.